湖南省株洲市茶陵县2022-2023学年八年级下学期期末数学数学考试试卷

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列交通标志图案中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 在Rt△ABC中，若一个锐角等于40°，则另一个锐角的度数为（　　）

A、40° B、45° C、50° D、60°

查看试题解析
3. 下列各组数分别为一个三角形三边的长，其中能构成直角三角形的一组是（　　）

A、2，3，4 B、6，8，10 C、5，12，14 D、1，1，2

查看试题解析
4. 若把点A(－5m，2m－1)向上平移3个单位后得到的点在x轴上，则点A在(　　)

A、x轴上 B、第三象限 C、y轴上 D、第四象限

查看试题解析
5. 小文同学统计了他所在小区居民每天微信阅读的时间，并绘制了直方图．①小文同学一共统计了60人；②每天微信阅读不足20分钟的人数有12人；③每天微信阅读30-40分钟的人数最多；④每天微信阅读0-10分钟的人数最少．根据图中信息，上述说法中正确的是（　　）

A、①②③④ B、①②③ C、②③④ D、③④

查看试题解析
6. 如图，在平面直角坐标系中，平行四边形 $A B C D$ 的顶点 $A$ 、 $B$ 、 $D$ 的坐标分别是 $(0 ， 0)$ 、 $(5 ， 0)$ 、 $(2 ， 3)$ ，则点 $C$ 的坐标是（　　）

A、 $(8 ， 2)$ B、 $(5 ， 3)$ C、 $(7 ， 3)$ D、 $(3 ， 7)$

查看试题解析
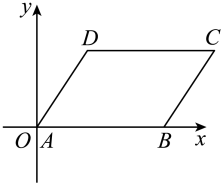7. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O ．下列条件不能判定平行四边形ABCD为矩形的是（）

A、 $A D = B C$ ， $A B / / C D$ B、 $A C = B D$ C、 $∠ B A D = ∠ A D C$ D、 $∠ A B C = 90 °$

查看试题解析
8. 一次函数 $y = k x + k$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析
9. 如图，菱形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点O ， E为边 $B C$ 的中点，连结 $O E$ ．若 $A C = 6 ， B D = 8$ ，则 $O E =$ （）

A、2 B、 $\frac{5}{2}$ C、3 D、4

查看试题解析
10. 如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，ED⊥AB于D.如果∠A＝30°，AE＝6cm，那么CE等于（）

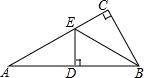A、 $\sqrt{3}$ cm B、2cm C、3cm D、4cm

查看试题解析

二、填空题

11. 如果一个多边形的内角和是外角和的5倍，那么这个多边形的边数是.

查看试题解析
12. 已知△ABC中，D、E分别是AB、AC边上的中点，且DE＝3cm，则BC＝cm．

查看试题解析
13. 若一组数据 $8$ ， $9$ ， $7$ ， $8$ ， $x$ ， $3$ 的平均数是 $7$ ，则这组数据的众数是。

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D是AB的中点，且 $D C = 5 cm$ ，则AB＝cm．

查看试题解析
15. 如图是天安门广场周围的主要景点分布示意图，在此图中建立平面直角坐标系，若表示故宫的点的坐标为（0，-1），表示美术馆的点的坐标为（2，2），则人民大会堂的坐标为．

查看试题解析
16. 请写出一个一次函数表达式，使此函数满足：①y随x的增大而减小；②函数图象过点（0，2），你写的函数表达式是．

查看试题解析
17. 将直线 $y = 2 x$ 向右平移2个单位，再向上平移3个单位后，所得的直线的表达式为．

查看试题解析
18. 如图，在菱形 $A B C D$ 中，对角线 $A C ， B D$ 交于点 $O$ ，过点 $A$ 作 $A H ⊥ B C$ 于点 $H$ ，已知BO=4，S_菱形ABCD=24，则 $A H =$ ．

查看试题解析

三、解答题

19. 已知一次函数的图象经过A(0，4)与B(－3，0)两点．

(1)、求这个一次函数的解析式；

(2)、判断点C(1， $\frac{8}{3}$ )与点D(3，8)是否在该一次函数的图象上．

查看试题解析
20. 如图， $A (- 3 ， 2)$ ， $B (- 1 ， - 2)$ ， $C (1 ， - 1)$ ．将 $△ A B C$ 向右平移 $3$ 个单位长度，然后再向上平移 $1$ 个单位长度，可以得到 $△ A_{1} B_{1} C_{1}$ ．

(1)、请在图中画出 $△ A_{1} B_{1} C_{1}$

(2)、 $△ A_{1} B_{1} C_{1}$ 的顶点 $A_{1}$ 的坐标为，顶点 $C_{1}$ 的坐标为．

(3)、 $△ A_{1} B_{1} C_{1}$ 的面积为．

(4)、已知点 $P$ 在 $x$ 轴上，以 $A_{1}$ 、 $C_{1}$ 、 $P$ 为顶点的三角形面积为 $\frac{3}{2}$ ，则 $P$ 点的坐标为．

查看试题解析
21. 如图，在△ABC和△DCB中，∠A＝∠D＝90°，AC＝BD，AC与BD相交于点O.

(1)、求证：△ABC≌△DCB；

(2)、△OBC是何种三角形？证明你的结论.

查看试题解析
22. 如图，直线 $l_{1}$ ：y＝2x-3与x轴交于点A ，直线 $l_{2}$ 经过点B（4，0），C（0，2），与 $l_{1}$ 交于点D ．

(1)、求直线 $l_{2}$ 的解析式；

(2)、求△ABD的面积．

查看试题解析

23. 某校举行了“文明在我身边”摄影比赛．已知每幅参赛作品成绩记为x分(60≤x＜100)．校方从600幅参赛作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制了如下不完整的统计图表．

分数段	频数	频率
60≤x<70	18	0.36
70≤x<80	17	c
80≤x<90	a	0.24
90≤x<100	b	0.06
合计		1

根据以上信息解答下列问题：

(1)、统计表中c的值为；样本成绩的中位数落在分数段中；

(2)、补全频数直方图；

(3)、若80分以上(含80分)的作品将被组织展评，试估计全校被展评的作品数量是多少．

查看试题解析

24. 如图，在平行四边形ABCD中，CE⊥AD于点E，延长DA至点F，使得EF＝DA，连接BF，CF．

(1)、求证：四边形BCEF是矩形；

(2)、若AB＝3，CF＝4，DF＝5，求EF的长．

查看试题解析
25. 为了响应国家节能减排的号召，鼓励市民节约用电，我市从2012年7月1日起，居民用电实行“一户一表”的“阶梯电价”，分三个档次收费，第一档是用电量不超过180千瓦时实行“基本电价”，第二、三档实行“提高电价”，具体收费情况如图的折线图，请根据图像回答下列问题；

(1)、当用电量是180千瓦时时，电费是元；

(2)、第二档的用电量范围是；

(3)、“基本电价”是元/千瓦时；

(4)、小明家8月份的电费是328.5元，这个月他家用电多少千瓦时？

查看试题解析
26. 如图，在Rt△ABC中，∠B=90°，BC=5 $\sqrt{3}$ ，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．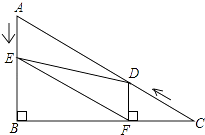

(1)、求证：AE=DF；

(2)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．

(3)、当t为何值时，△DEF为直角三角形？请说明理由．

查看试题解析