湖南省长沙市雨花区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 已知是关于x的一元二次方程的一个根,则m的值是( )A、 B、0 C、1 D、22. 若正比例函数的图象经过点 ,则这个图象必经过点( )A、 B、 C、 D、3. 如图,菱形ABCD中, ,则 ( )
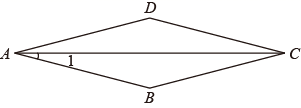 A、30° B、25° C、20° D、15°4. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-kx+k的图象大致是( )A、
A、30° B、25° C、20° D、15°4. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-kx+k的图象大致是( )A、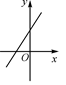 B、
B、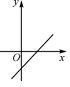 C、
C、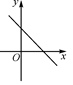 D、
D、 5. 在平面直角坐标系中,把直线y=3x向左平移2个单位长度,平移后的直线解析式是( )A、y=3x+2 B、y=3x-2 C、y=3x+6 D、y=3x-66. 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
5. 在平面直角坐标系中,把直线y=3x向左平移2个单位长度,平移后的直线解析式是( )A、y=3x+2 B、y=3x-2 C、y=3x+6 D、y=3x-66. 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( ) A、9cm B、12cm C、15cm D、18cm7. 如图,点分别是四边形边的中点.则正确的是( )
A、9cm B、12cm C、15cm D、18cm7. 如图,点分别是四边形边的中点.则正确的是( )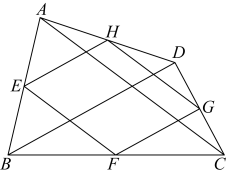 A、若 , 则四边形为矩形 B、若 , 则四边形为菱形 C、若是平行四边形,则与互相平分 D、若是正方形,则与互相垂直且相等8. 若关于 的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )
A、若 , 则四边形为矩形 B、若 , 则四边形为菱形 C、若是平行四边形,则与互相平分 D、若是正方形,则与互相垂直且相等8. 若关于 的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )
A、 B、1 C、 D、9. 《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为 ( )A、 B、 C、 D、10. 某班级共有41人,在一次体质测试中,有1人未参加集体测试,老师对集体测试的成绩按40人进行了统计,得到测试成绩分数的平均数是88,中位数是85.缺席集体测试的同学后面进行了补测,成绩为88分,关于该班级41人的体质测试成绩,下列说法正确的是( )A、平均数不变,中位数变大 B、平均数不变,中位数无法确定 C、平均数变大,中位数变大 D、平均数不变,中位数变小二、填空题
-
11. 设 , 是一元二次方程 的两根,则 .12. 在某校举办的队列比赛中,A班的成绩如下:
项目
着装
队形
精神风貌
成绩/分
90
95
95
若按着装占10%、队形占60%、精神风貌占30%计算参赛班级的综合成绩,则班的最后得分是分.
13. 如图,已知菱形 的对角线 交于点 为 的中点,若 ,则菱形的周长为.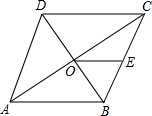 14. 已知一次函数y=kx+b的图象经过一,二,四象限,且当2≤x≤4时,4≤y≤6,则的值是 .15. 如图,在 中, , , ,AD是 的平分线.若P,Q分别是AD和AC上的动点,则 的最小值是.
14. 已知一次函数y=kx+b的图象经过一,二,四象限,且当2≤x≤4时,4≤y≤6,则的值是 .15. 如图,在 中, , , ,AD是 的平分线.若P,Q分别是AD和AC上的动点,则 的最小值是.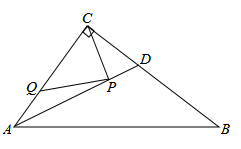 16. 如图,一次函数的图象过点 , 且与x轴相交于点B . 若点P是x轴上的一点,且满足△APB是等腰三角形,则点P的坐标可以是 .
16. 如图,一次函数的图象过点 , 且与x轴相交于点B . 若点P是x轴上的一点,且满足△APB是等腰三角形,则点P的坐标可以是 .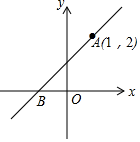
三、解答题
-
17. 解方程: .18. 已知直角三角形的三边长是三个连续自然数,求三边长.19. 已知y是x的一次函数,表中给出了部分对应值.
x
-1
2
4
n
y
5
-1
m
-7
(1)、求该一次函数的表达式;(2)、求m,n的值.20. 为了加强对青少年防溺水安全教育,4月初某校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.下面是从参赛学生中随机收集到的20名学生的成绩(单位:分):87 99 86 89 91 91 95 96 87 97
91 97 96 86 96 89 100 91 99 97
整理数据:
成绩(分)
86
87
89
91
95
96
97
99
100
学生人数(人)
2
2
2
4
1
3
3
2
1
分析数据:
平均数
众数
中位数
93
a
b
解决问题:
(1)、直接写出:上面表格中的 , ;(2)、若成绩达到95分及以上为“优秀”等级,求“优秀”等级所占的百分率为;(3)、请估计该校1500名学生中成绩达到95分及以上的学生人数.21. 据统计,目前某市基站的数量约万座,计划到2023年底,全市基站数是目前的4倍,到2025年底,全市基站数最将达到万座.(1)、计划到2023年底,全市基站的数量是多少万座?(2)、求2023年底到2025年底,全市基站数量的年平均增长率.22. 如图,已知直线y=kx+b经过点A(5,0),B(1,4).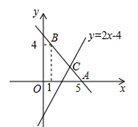 (1)、求直线AB的解析式;(2)、若直线y=2x-4与直线AB相交于点C,求点C的坐标.23. 如图,中,点D是AB上一点,点E是AC的中点,过点C作 , 交DE的延长线于点F.
(1)、求直线AB的解析式;(2)、若直线y=2x-4与直线AB相交于点C,求点C的坐标.23. 如图,中,点D是AB上一点,点E是AC的中点,过点C作 , 交DE的延长线于点F.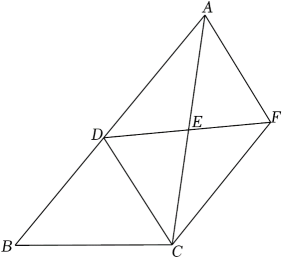 (1)、求证:;(2)、连接AF,CD.如果点D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF是菱形,证明你的结论.24. 请阅读下列材料:
(1)、求证:;(2)、连接AF,CD.如果点D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF是菱形,证明你的结论.24. 请阅读下列材料:问题:已知方程 , 求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为 , 则 , 所以 , 把代入已知方程,得;化简,得;故所求方程为 .
这种利用方程根的代换求新方程的方法,我们称为“换根法”;
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)、已知方程 , 求一个一元二次方程,使它的根分别为已知方程根的相反数;(2)、已知关于的一元二次方程有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.25. 已知:四边形ABCD是正方形, , 点E , F , G , H分别在边AB , BC , AD , DC上.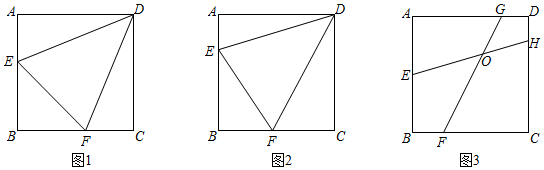 (1)、如图1,若 , , 则的度数为;(2)、如图2,若 , 点E , F分别是AB , BC上的动点,求的周长;(3)、如图3,若 , GF和EH交于点O , 且 , 求EH的长度.
(1)、如图1,若 , , 则的度数为;(2)、如图2,若 , 点E , F分别是AB , BC上的动点,求的周长;(3)、如图3,若 , GF和EH交于点O , 且 , 求EH的长度.