湖南省长沙市望城区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 以下计算正确的是（）

A、 $202 3^{0} = 0$ B、 $\sqrt{7} + \sqrt{6} = \sqrt{13}$ C、 ${(- 3 a^{2})}^{3} = - 27 a^{5}$ D、 $a^{7} \div a^{3} = a^{4}$

查看试题解析
2. 在平面直角坐标系中，点 $P (3 ， 4)$ ，则点P到原点的距离为（）

A、3 B、 $- 5$ C、5 D、4

查看试题解析
3. 如图， $▱ O A B C$ 位于第一象限中，已知顶点A、C的坐标分别为 $(5 ， 0)$ ， $(2 ， 3)$ ，则顶点B的坐标为（）

A、 $(5 ， 3)$ B、 $(6 ， 3)$ C、 $(6 ， 4)$ D、 $(7 ， 3)$

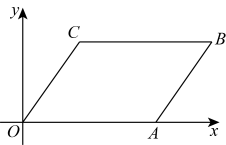查看试题解析
4. 已知一组数据3、8、5、 $x$ 、4的众数为4，则该组数据的中位数为（）

A、3 B、4 C、5 D、8

查看试题解析
5. 已知 $y = k x + b$ ，当 $x = 0$ 时， $y = - 1$ ；当 $x = \frac{1}{2}$ 时， $y = 2$ ，那么当 $x = - \frac{1}{2}$ 时， $y$ 的值为（）

A、 $- 2$ B、 $- 3$ C、 $- 4$ D、2

查看试题解析
6. 古希腊几何学家海伦和我国南宋数学家秦九韶曾提出利用三角形的三边求面积的公式，称为海伦-秦九韶公式：如果一个三角形的三边长分别是a，b，c，记 $p = \frac{a + b + c}{2}$ ，那么三角形的面积为 $S = \sqrt{p (p - b) (p - a) (p - c)}$ .如图，在 $△ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 所对的边分别为a，b，c，若 $a = 3$ ， $b = 5$ ， $c = 6$ ，则 $△ A B C$ 的面积为（）

A、 $\sqrt{14}$ B、 $2 \sqrt{14}$ C、 $3 \sqrt{14}$ D、 $4 \sqrt{14}$

查看试题解析
7. 如图，把图1中边长为10的菱形沿对角线分成四个全等的直角三角形，且此菱形的一条对角线长为16，将这四个直角三角形拼成如图2所示的正方形，则图2中的阴影面积为（）

A、2 B、4 C、9 D、16

查看试题解析
8. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩是0.9环．方差分别0.56、0.78、0.42、0.63，这四人中成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 如图，有两棵垂直于地面的树，一棵高8米，另一棵高2米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，则它至少要飞行（　　）米．

A、6 B、8 C、10 D、12

查看试题解析
10. 已知 $A (a ， b) 、 B (c ， d)$ 是一次函数 $y = k x - 2 x - 1$ 图象上的不同的两个点，若 $(c - a) (d - b) < 0$ ，则k的取值范围是（　　）

A、 $k < 3$ B、 $k > 3$ C、 $k < 2$ D、 $k > 2$

查看试题解析

二、填空题

11. 若a ， b都是实数， $b = \sqrt{1 - 2 a} + \sqrt{2 a - 1} + 3$ ，则 $a^{b}$ 的值为．

查看试题解析
12. 已知正比例函数 $y = k x$ 中，y的值随x的增大而增大，则 $(\sqrt{3} ， k)$ 在第象限．

查看试题解析
13. 如图，在 $R t$ $△ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ 是斜边 $A B$ 的中点， $D E$ 平分 $∠ A D C ， B C = 4$ ，则 $D E$ 的长是．

查看试题解析
14. 函数 $y = \frac{1 - x}{\sqrt{x + 2}}$ 中自变量x的取值范围是．

查看试题解析
15. 观察以下几组勾股数，并寻找规律：请你写出有以上规律的第⑤组勾股数：．
①3；4；5；

②5；12；13；

③7；24；25；

④9；40；41......

查看试题解析
16. 如图，正方形 $A B C D$ 的对角线相交于点 $O$ ，点 $O$ 又是正方形 $A_{1} B_{1} C_{1} O$ 的一个顶点，而且这两个正方形的边长都等于2，无论正方形 $A_{1} B_{1} C_{1} O$ 绕点 $O$ 怎样转动，两个正方形重叠部分的面积都不变，则这两个正方形重叠部分的面积为．

查看试题解析

三、解答题

17. 计算： $\sqrt{6} \div \sqrt{2} + | 1 - \sqrt{3} | - \sqrt{12} + {(\frac{1}{2})}^{- 1}$ ；

查看试题解析
18. 如图，矩形ABCD的对角线AC、BD相交于点O ， $A E ⊥ B D$ ，垂足为E ， $∠ A O B = 56 °$ ，求 $∠ E A B$ 的度数．

查看试题解析
19. 填表，并在如图的平面直角坐标系中画出一次函数 $y = x + 2$ 的图象．

(1)、列表：
          $x$
          $- 1$
0
          $y = x + 2$

(2)、描点、连线：


查看试题解析
20. 体育课上，老师为了解女学生定点投篮的情况，随机搶取8名女生进行每人4次定点投篮的测试，进球数的统计如图所示．

(1)、求女生进球数的平均数、中位数、众数；

(2)、投球4次，进球3个以上（含3个）为优秀，全校有女生800人，估计为“优秀”等级的女生约为多少人？

查看试题解析
21. 已知点 $A (8 ， 0)$ 及在第一象限的动点 $P (x ， y)$ ，且 $x + y = 10$ ．设 $△ O P A$ 的面积为 $S$ ．

(1)、求 $S$ 关于 $x$ 的函数解析式；

(2)、求 $x$ 的取值范围，并根据 $x$ 的取值范围求出 $S$ 的取值范围；

(3)、当 $S = 12$ 时，求 $P$ 点坐标．

查看试题解析
22. 近年来，我国着力促进教育公平，提升教育质量，加快推进教育现代化、建设教育强国、办好人民满意的教育，教育数字化工作持续推进、成果丰硕．在教育数字化进程中，多媒体的作用不可小觑．某教育科技公司销售 $A$ ， $B$ 两种多媒体教学设备，这两种多媒体设备的进价与售价如表所示：

A

B

进价（万元/套）

3

2.4

售价（万元/套）

3.3

2.8

该教育科技公司计划购进 $A$ ， $B$ 两种多媒体设备共 $50$ 套，设购进 $A$ 种多媒体设备x套，利润为y万元

(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、若公司要求购进 $B$ 种多媒体设备的数量不超过 $A$ 种多媒体设备的 $4$ 倍，当该公司把购进的两种多媒体设备全部售出，求购进 $A$ 种多媒体设备多少套时，能获得最大利润，最大利润是多少万元？

查看试题解析
23.

(1)、已知 $m = \sqrt[b - 1]{a + 4}$ 是 $a + 4$ 的算术平方根， $n = \sqrt[a - 2]{3 b - 1}$ 是 $3 b - 1$ 的立方根，求 $m - 2 n$ 的立方根；

(2)、若 $m = \sqrt{1 - a} + \sqrt{a - 1} + 1$ ， $n$ 的算术平方根是5，求 $3 n + 6 m$ 的平方根．

查看试题解析
24. 某校数学兴趣小组活动：用一张矩形纸片剪出一张菱形纸片，要求菱形的各个顶点均落在矩形的边或顶点上，例如：过矩形两对角线的交点，作两条互相垂直的直线与矩形四边相交，依次连结四个交点，沿连线可剪出菱形．

(1)、请画2种符合要求的示意图；

(2)、若 $A B = 6 c m$ ， $B C = 8 c m$ ，求出你所作的其中一个菱形的边长．

查看试题解析
25. 在平面直角坐标系中，已知一次函数 $y = \frac{1}{2} x + 1$ 的图象与 $x$ 轴、 $y$ 轴分别交于 $A ， B$ 两点．以 $A B$ 为边在第二象限内作正方形 $A B C D$ ．

(1)、求点 $C$ ， $D$ 的坐标；

(2)、在 $x$ 轴上是否存在点 $M$ ，使 $△ M D B$ 的周长最小？若存在，请求出点 $M$ 的坐标；若不存在，请说明理由．

查看试题解析

$x$	$- 1$	0
$y = x + 2$

	A	B
进价（万元/套）	3	2.4
售价（万元/套）	3.3	2.8