湖南省长沙市浏阳市2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 要使二次根式有意义,则x的取值范围为( )A、 B、 C、 D、2. 下列函数中,属于正比例函数的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 下列几组数中,不能作为直角三角形三边长的是( )A、 , , B、 , , C、 , , D、 , ,5. 如图,在中,对角线和相交于点 , 添加下列条件不能判定四边形是菱形的是( )
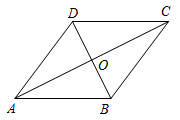 A、 B、 C、平分 D、6. 年3月5日-3月13日,全国两会在首都北京召开,为了让学生更好地了解两会,某学校组织了一次关于“全国两会”的知识比赛,在抢答赛初赛中,某班4个小队的成绩统计结果如下表:
A、 B、 C、平分 D、6. 年3月5日-3月13日,全国两会在首都北京召开,为了让学生更好地了解两会,某学校组织了一次关于“全国两会”的知识比赛,在抢答赛初赛中,某班4个小队的成绩统计结果如下表:第1队
第2队
第3队
第4队
平均分
方差
要从4个小队中选出一个小队代表班级参加决赛,应该选哪个队伍参赛比较合理?( )
A、第1队 B、第2队 C、第3队 D、第4队7. 如图,在中, , 于点E , , , 则的度数为( )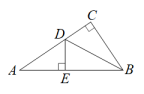 A、34° B、36° C、38° D、40°8. 如图,四边形是平行四边形, , 平分且交于点E , 且交于点F , 则( )
A、34° B、36° C、38° D、40°8. 如图,四边形是平行四边形, , 平分且交于点E , 且交于点F , 则( )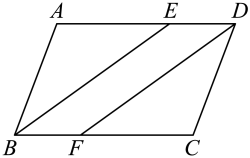 A、 B、 C、 D、9. 、两地相距 , 甲、乙两人沿同一条路从A地到地. , 分别表示甲、乙两人离开地的距离()与时间()之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地;③甲的速度是 , 乙的速度是;④当乙车出发2小时时,两车相距 . 其中正确的结论有( )
A、 B、 C、 D、9. 、两地相距 , 甲、乙两人沿同一条路从A地到地. , 分别表示甲、乙两人离开地的距离()与时间()之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地;③甲的速度是 , 乙的速度是;④当乙车出发2小时时,两车相距 . 其中正确的结论有( )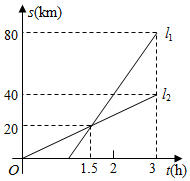 A、1个 B、2个 C、3个 D、4个10. 如图,已知点 , 点B是直线上的动点,点C是y轴上的动点,则的周长的最小值等于( )
A、1个 B、2个 C、3个 D、4个10. 如图,已知点 , 点B是直线上的动点,点C是y轴上的动点,则的周长的最小值等于( )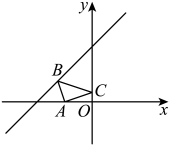 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 使是整数的正整数的最小值为 .12. 已知一个菱形的两条对角线的长分别为5cm和8cm,该菱形的面积为cm2 .13. 顺次连接对角线互相垂直的四边形的各边的中点所构成的四边形是.(填“平行四边形、矩形、菱形或正方形”)14. 一组数据:4,6,12分别以 , , 为权的加权平均数为 .15. 当时,对于的每一个值,一次函数的值都小于函数的值,则的取值范围为 .16. 如图,在正方形中,点E是边上的一点,点F在边的延长线上,且 , 连接交边于点G.过点A作 , 垂足为点M,交边于点N.若 , 则线段的长为 .
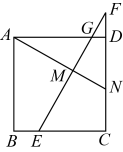
三、解答题
-
17. 计算: .18. 如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=x图象交于点P (2,n).
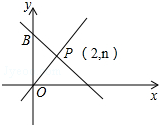 (1)、求m和n的值;(2)、求△POB的面积.19. 设一个三角形的三边分别为a , b , c , p=(a+b+c),则有下列面积公式:S=(海伦公式);S=(秦九韶公式).(1)、一个三角形的三边长依次为3,5,6,任选以上一个公式求这个三角形的面积;(2)、一个三角形的三边长依次为 , , , 任选以上一个公式求这个三角形的面积.20. 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)、求m和n的值;(2)、求△POB的面积.19. 设一个三角形的三边分别为a , b , c , p=(a+b+c),则有下列面积公式:S=(海伦公式);S=(秦九韶公式).(1)、一个三角形的三边长依次为3,5,6,任选以上一个公式求这个三角形的面积;(2)、一个三角形的三边长依次为 , , , 任选以上一个公式求这个三角形的面积.20. 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF. (1)、求证:△ADE≌△ABF;(2)、若BC=8,DE=6,求△AEF的面积.21. 某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按元/计B类收费标准如下:没有月租费,但通话费按元/计.(1)、设通话时间为x和手机话费为y , 请写出A , B两种计费方式分别对应的函数表达式.(2)、月通话时间为多长时,两种套餐收费一样?(3)、若每月平均通话时长为300分钟,选择哪类收费方式较少?请说明理由.22. 如图,平面直角坐标系中,点为坐标原点,已知三个顶点坐标分别为 , , . 将向左平移4个单位得到 , 点A , B , C的对应点分别是 , , .
(1)、求证:△ADE≌△ABF;(2)、若BC=8,DE=6,求△AEF的面积.21. 某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按元/计B类收费标准如下:没有月租费,但通话费按元/计.(1)、设通话时间为x和手机话费为y , 请写出A , B两种计费方式分别对应的函数表达式.(2)、月通话时间为多长时,两种套餐收费一样?(3)、若每月平均通话时长为300分钟,选择哪类收费方式较少?请说明理由.22. 如图,平面直角坐标系中,点为坐标原点,已知三个顶点坐标分别为 , , . 将向左平移4个单位得到 , 点A , B , C的对应点分别是 , , .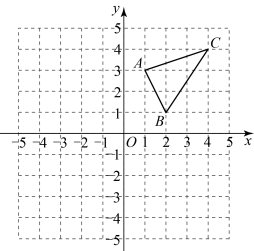 (1)、请在图中画出;(2)、求的面积;(3)、若且轴,则点的坐标为 .23. 某校为了解学生利用课余时间参加义务劳动的情况,随机调查了部分学生参加义务劳动的时间(单位:h).根据统计的结果,绘制出如下的统计图①和图②.
(1)、请在图中画出;(2)、求的面积;(3)、若且轴,则点的坐标为 .23. 某校为了解学生利用课余时间参加义务劳动的情况,随机调查了部分学生参加义务劳动的时间(单位:h).根据统计的结果,绘制出如下的统计图①和图②.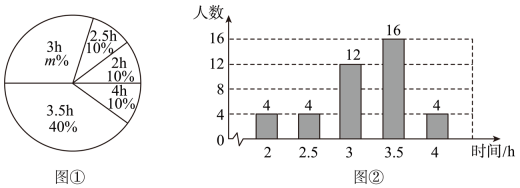
请根据相关信息,解答下列问题;
(1)、本次接受随机抽样调查的学生人数为 , 图①中的m的值为;(2)、求统计的这组数据的平均数、众数和中位数;(3)、若该校有400名学生参加了义务劳动,估计其中劳动时间大于的学生人数.24. 如图,在等边中, , 点为边上一点,点为边上一点,连接 .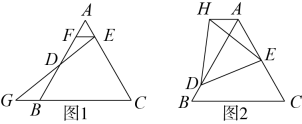 (1)、如图1,过点作交于点 , 延长交延长线于点 , 若 , 求的长;(2)、如图2,将绕点逆时针旋转60°得到 , 连接 , 请猜想、、的数量关系并证明;25. 综合题
(1)、如图1,过点作交于点 , 延长交延长线于点 , 若 , 求的长;(2)、如图2,将绕点逆时针旋转60°得到 , 连接 , 请猜想、、的数量关系并证明;25. 综合题如图1,为直线上一点,过点作射线 , , 将一直角三角板()的直角顶点放在点处,一边在射线上,另一边与都在直线的上方.
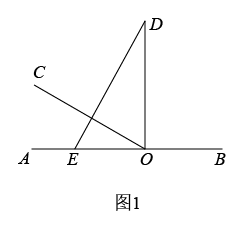 (1)、将图1中的三角板绕点以每秒的速度沿顺时针方向旋转一周,如图2,经过秒后,恰好平分 .
(1)、将图1中的三角板绕点以每秒的速度沿顺时针方向旋转一周,如图2,经过秒后,恰好平分 .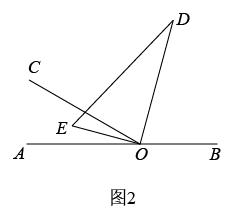
①此时的值为;(直接填空)
②此时是否平分?请说明理由.
(2)、在(1)问的基础上,若三角板在转动的同时,射线也绕点以每秒的速度沿顺时针方向旋转一周,如图3,那么经过多长时间平分?请说明理由; (3)、在(2)问的基础上,经过多长时间平分?
(3)、在(2)问的基础上,经过多长时间平分?