湖南省岳阳市岳阳楼区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点(﹣1,3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 对某班学生在家做家务的时间进行调查后,将所得数据分成4组,第一组的频率为0.15,第二组和第三组的频率之和为0.75,则第四组的频率为( )A、0.35 B、0.30 C、0.20 D、0.104. 在函数中,当自变量时,函数值等于( )A、1 B、4 C、7 D、135. 已知一个多边形的内角和为540°,则这个多边形为( )A、三角形 B、四边形 C、五边形 D、六边形6. 下列有关一次函数的说法中,正确的是( )A、的值随着值的增大而增大 B、函数图象与轴的交点坐标为 C、当时, D、函数图象经过第二、三、四象限7. 下列命题中,不正确的是( )A、斜边和一条直角边对应相等的两个直角三角形全等 B、若是y关于x的一次函数,则m的值为2 C、在建立了平面直角坐标系后,平面上的点与有序实数对一一对应 D、矩形的对角线互相垂直8. 图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形 . 若 , 且 , 则的长度为( )
3. 对某班学生在家做家务的时间进行调查后,将所得数据分成4组,第一组的频率为0.15,第二组和第三组的频率之和为0.75,则第四组的频率为( )A、0.35 B、0.30 C、0.20 D、0.104. 在函数中,当自变量时,函数值等于( )A、1 B、4 C、7 D、135. 已知一个多边形的内角和为540°,则这个多边形为( )A、三角形 B、四边形 C、五边形 D、六边形6. 下列有关一次函数的说法中,正确的是( )A、的值随着值的增大而增大 B、函数图象与轴的交点坐标为 C、当时, D、函数图象经过第二、三、四象限7. 下列命题中,不正确的是( )A、斜边和一条直角边对应相等的两个直角三角形全等 B、若是y关于x的一次函数,则m的值为2 C、在建立了平面直角坐标系后,平面上的点与有序实数对一一对应 D、矩形的对角线互相垂直8. 图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形 . 若 , 且 , 则的长度为( ) A、 B、 C、4 D、9. 某航空公司规定,旅客乘机所携带的行李的质量与其运费y(元)有如图所示的一次函数图形确定,那么旅客所携带免费行李的最大质量为( )
A、 B、 C、4 D、9. 某航空公司规定,旅客乘机所携带的行李的质量与其运费y(元)有如图所示的一次函数图形确定,那么旅客所携带免费行李的最大质量为( ) A、15kg B、20kg C、25kg D、30kg10. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )
A、15kg B、20kg C、25kg D、30kg10. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )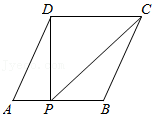 A、
A、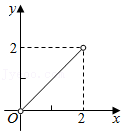 B、
B、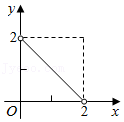 C、
C、 D、
D、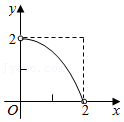
二、填空题
-
11. 函数y= 的自变量x的取值范围是 .12. 若点 在 轴上,则点 的坐标为.13. 把直线向上平移3个单位后所得直线的函数关系式为 .14. 在▱中,对角线 , 相交于点 , 点为的中点,如果▱周长为 , , 那么 .
 15. 如图,平行四边形中,在上截取 , 分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 连接交于 , 若 , , 则的长为 .
15. 如图,平行四边形中,在上截取 , 分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 连接交于 , 若 , , 则的长为 . 16. 如图,在平面直角坐标系中,函数和的图象分别为直线和 , 过点作轴的垂线交于点 , 过点作y轴的垂线交于点 , 过点作x轴的垂线交于点 , 过点作y轴的垂线交于点 , …依次进行下去,则点的坐标为 .
16. 如图,在平面直角坐标系中,函数和的图象分别为直线和 , 过点作轴的垂线交于点 , 过点作y轴的垂线交于点 , 过点作x轴的垂线交于点 , 过点作y轴的垂线交于点 , …依次进行下去,则点的坐标为 .
三、解答题
-
17. 如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3).
 (1)、把△ABC向右平移5个单位,再向下平移3个单位得到△ , 请在图中作出△ , 点的坐标为;(2)、请在图中作出△ABC关于x轴对称的△ , 点的坐标为;18. 如图,平行四边形的两条对角线相交于点O ,
(1)、把△ABC向右平移5个单位,再向下平移3个单位得到△ , 请在图中作出△ , 点的坐标为;(2)、请在图中作出△ABC关于x轴对称的△ , 点的坐标为;18. 如图,平行四边形的两条对角线相交于点O , (1)、求证:平行四边形是菱形;(2)、求菱形的面积.19. 已知直线交x轴于点A , 交y轴于点B . 直线交x轴于点D , 与直线相交于点C .
(1)、求证:平行四边形是菱形;(2)、求菱形的面积.19. 已知直线交x轴于点A , 交y轴于点B . 直线交x轴于点D , 与直线相交于点C .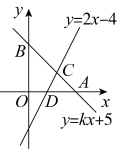 (1)、直接写出关于x的不等式的解集;(2)、求直线的解析式;(3)、求的面积.20. 如图,在中, , , , 和分别是斜边上的中线和高线,是的中点.
(1)、直接写出关于x的不等式的解集;(2)、求直线的解析式;(3)、求的面积.20. 如图,在中, , , , 和分别是斜边上的中线和高线,是的中点. (1)、求的长;(2)、证明:为等边三角形.21. 某校为推进 “学党史、强信念、跟党走”学习教育,组织了一次全校学生的党史知识大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
(1)、求的长;(2)、证明:为等边三角形.21. 某校为推进 “学党史、强信念、跟党走”学习教育,组织了一次全校学生的党史知识大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:成绩/分
频数
频率
10
0.05
20
0.10
30
0.30
80
0.40

请根据所给信息,解答下列问题:
(1)、 , ;(2)、请补全频数分布直方图;(3)、若成绩在80分以上(包括80分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?22. 如图,四边形的对角线 , 相交于点 , 其中 , , , 为上的一点,连接 , . (1)、求证:四边形是矩形;(2)、若平分 , 且 , 求的度数.23. 如图①是甲,乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度与注水时间之间的关系如图②所示,根据图像解答下列问题:
(1)、求证:四边形是矩形;(2)、若平分 , 且 , 求的度数.23. 如图①是甲,乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度与注水时间之间的关系如图②所示,根据图像解答下列问题: (1)、图②中折线表示槽中水的深度与注入时间之间的关系;线段表示槽中水的深度与注入时间之间的关系;铁块的高度为cm.(2)、注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)24. “先天下之忧而忧,后天下之乐而乐”这是《岳阳楼记》中的一句千古名言,也是岳阳精神的真实写照,这句话具有鲜明的对称美.如果一个凸四边形沿着它的一条对角线对折后能完全重合,我们就把这个四边形称为“忧乐四边形”.如图1,凸四边形沿对角线对折后完全重合,四边形是以直线为对称轴的“忧乐四边形”.
(1)、图②中折线表示槽中水的深度与注入时间之间的关系;线段表示槽中水的深度与注入时间之间的关系;铁块的高度为cm.(2)、注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)24. “先天下之忧而忧,后天下之乐而乐”这是《岳阳楼记》中的一句千古名言,也是岳阳精神的真实写照,这句话具有鲜明的对称美.如果一个凸四边形沿着它的一条对角线对折后能完全重合,我们就把这个四边形称为“忧乐四边形”.如图1,凸四边形沿对角线对折后完全重合,四边形是以直线为对称轴的“忧乐四边形”.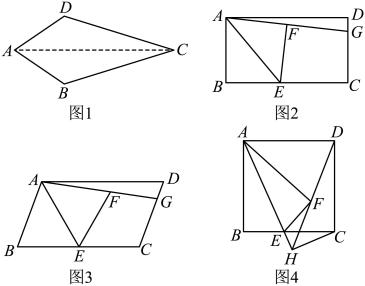 (1)、下列四边形一定是“忧乐四边形”的有(填序号)
(1)、下列四边形一定是“忧乐四边形”的有(填序号)①平行四边形;②长方形;③正方形;④菱形;⑤梯形
(2)、在四边形中,点E是边上的中点,四边形是以直线为对称轴的“忧乐四边形”(点F在四边形内部),连接并延长交于点G .①如图2,若四边形是矩形,求证:四边形是“忧乐四边形”.
②如图3,若四边形是平行四边形,①中的结论是否仍然成立,请说明理由.
(3)、如图4,四边形是正方形,且点E为线段上的动点(不与B、C重合),四边形是以直线为对称轴的“忧乐四边形”(点F在正方形内部),连接并延长,与的延长线交于点H , 连接 , 请直接写出三条线段之间的数量关系.25. 如图1,等腰直角三角形中, , 直线经过点C , 过A作于点D . 过B作E于点E , 则 , 这是我们熟悉的一线三直角模型,我们称这种全等模型为“k字型全等”.若一次函数的图象与x轴、y轴分别交于A、B两点. (1)、如图2,当时,若点B到经过原点的直线l的距离的长为3,求点A到直线l的距离的长;(2)、如图3,当时,点M在第一象限内,若是以为斜边的等腰直角三
(1)、如图2,当时,若点B到经过原点的直线l的距离的长为3,求点A到直线l的距离的长;(2)、如图3,当时,点M在第一象限内,若是以为斜边的等腰直角三角形,求点M的坐标;
(3)、我们知道:随着k值的变化,点A的位置也会变化.若 , 如图4,将线段绕点B逆时针旋转后得到线段①当B、O、三点构成等腰三角形时,求点的坐标及k的值.
②若是钝角三角形,请直接写出k的取值范围.