湖南省岳阳市岳阳县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 将四个数字看作一个图形,则下列四个图形中,是中心对称图形的是( )A、
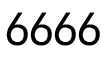 B、
B、 C、
C、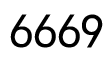 D、
D、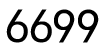 2. 在平面直角坐标系的第二象限内有一点P,它到x轴的距离为3,到y轴的距离为5,则点P的坐标为( )A、(-5,3) B、(-3,5) C、(3,5) D、(5,-3)3. 某学校有教职工90名,按他们的年龄分成10组,在40~45(岁)组内有教职工18名,那么这个小组的频率是( )A、 B、 C、 D、204. 一个多边形的内角和为900°,则这个多边形是( )A、七边形 B、八边形 C、九边形 D、十边形5. 下列结论中,菱形具有而矩形不一定具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对边相等且平行6. 直线 不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,在中, , 将经点顺时针旋转得到 , 连接 , 则的长为( )
2. 在平面直角坐标系的第二象限内有一点P,它到x轴的距离为3,到y轴的距离为5,则点P的坐标为( )A、(-5,3) B、(-3,5) C、(3,5) D、(5,-3)3. 某学校有教职工90名,按他们的年龄分成10组,在40~45(岁)组内有教职工18名,那么这个小组的频率是( )A、 B、 C、 D、204. 一个多边形的内角和为900°,则这个多边形是( )A、七边形 B、八边形 C、九边形 D、十边形5. 下列结论中,菱形具有而矩形不一定具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对边相等且平行6. 直线 不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,在中, , 将经点顺时针旋转得到 , 连接 , 则的长为( ) A、5 B、8 C、10 D、128. 在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )A、y=3x+5 B、y=3x﹣5 C、y=3x+1 D、y=3x﹣19. 如图,在 中, ,由图中的尺规作图痕迹得到的射线 与 交于点E , 点F为 的中点,连接 ,若 ,则 的周长为( )
A、5 B、8 C、10 D、128. 在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )A、y=3x+5 B、y=3x﹣5 C、y=3x+1 D、y=3x﹣19. 如图,在 中, ,由图中的尺规作图痕迹得到的射线 与 交于点E , 点F为 的中点,连接 ,若 ,则 的周长为( ) A、 B、 C、 D、410. 下是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是( )A、由②推出③,由③推出① B、由①推出②,由②推出③ C、由③推出①,由①推出② D、由①推出③,由③推出②
A、 B、 C、 D、410. 下是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是( )A、由②推出③,由③推出① B、由①推出②,由②推出③ C、由③推出①,由①推出② D、由①推出③,由③推出②二、填空题
-
11. 一个多边形的每一个外角都为 , 则这个多边形的边数是 .12. 函数 中,自变量x的取值范围是 .13. 如果点在第二象限,那么的取值范围是 .14. 点关于y轴对称的点的坐标是 .15. 如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则矩形MNPQ的面积是 .
 16. 如图,在正方形中, , 为对角线上与 , 不重合的一个动点,过点作于点 , 于点 , 连接 , . 则下列结论:①;②;③;④的最小值为 . 其中正确的是 . (填写序号)
16. 如图,在正方形中, , 为对角线上与 , 不重合的一个动点,过点作于点 , 于点 , 连接 , . 则下列结论:①;②;③;④的最小值为 . 其中正确的是 . (填写序号)
三、解答题
-
17. 如图,的顶点坐标分别为 , , 将向右再向下平移后得到 , 且点A的对应点的坐标是 , 点B、的对应点分别是 .
 (1)、直接写出点的坐标;: , : .(2)、请在图中画出 .(3)、点之间的距离是 .18. 如图,已知点分别在平行四边形的边上,且 , 求证: .
(1)、直接写出点的坐标;: , : .(2)、请在图中画出 .(3)、点之间的距离是 .18. 如图,已知点分别在平行四边形的边上,且 , 求证: . 19. 小惠自编一题:“如图,在四边形中,对角线交于点 , , 求证:四边形是菱形”,并将自己的证明过程与同学小洁交流.
19. 小惠自编一题:“如图,在四边形中,对角线交于点 , , 求证:四边形是菱形”,并将自己的证明过程与同学小洁交流.小惠:证明:垂直平分 .
四边形是菱形.( )
小洁:这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠的证法,请在第一个方框内的( )中打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
 (1)、你补充的条件是:;(2)、证明:20. 某学校在本校开展了四项“课后服务”项目(项目:足球;项目:篮球;项目:跳绳;项目:书法),要求每名学生必选且只能选修其中一项,为了解学生的选修情况,学校决定进行抽样调查,并根据收集的数据绘制了图1和图2两幅不完整的统计图.
(1)、你补充的条件是:;(2)、证明:20. 某学校在本校开展了四项“课后服务”项目(项目:足球;项目:篮球;项目:跳绳;项目:书法),要求每名学生必选且只能选修其中一项,为了解学生的选修情况,学校决定进行抽样调查,并根据收集的数据绘制了图1和图2两幅不完整的统计图. (1)、本次调查的学生共有人;在扇形统计图中,所对应的扇形的圆心角的度数是;(2)、将条形统计图补充完整;(3)、若全校共有1200名学生, 估计该校选修篮球和跳绳两个项目的总人数.21. 如图,已知直线经过点 .
(1)、本次调查的学生共有人;在扇形统计图中,所对应的扇形的圆心角的度数是;(2)、将条形统计图补充完整;(3)、若全校共有1200名学生, 估计该校选修篮球和跳绳两个项目的总人数.21. 如图,已知直线经过点 . (1)、求的值;(2)、①当时,函数值为负数;
(1)、求的值;(2)、①当时,函数值为负数;②将这条直线沿轴向(填“上”或“下”)平移个单位长度,与正比例函数的图象重合.
22. 如图,在中,分别平分、 , 点在线段上,求证: . 23. 如图,四边形中, , 点 , 分别是 , 的中点. , 的位置关系如何?证明你的猜想.
23. 如图,四边形中, , 点 , 分别是 , 的中点. , 的位置关系如何?证明你的猜想. 24. A , B两地相距 , 甲、乙两人分别开车从A地出发前往B地,其中甲先出发 , 如图是甲,乙行驶路程随行驶时间变化的图象,请结合图象信息.解答下列问题:
24. A , B两地相距 , 甲、乙两人分别开车从A地出发前往B地,其中甲先出发 , 如图是甲,乙行驶路程随行驶时间变化的图象,请结合图象信息.解答下列问题: (1)、分别求出与之间的函数解析式;(2)、求出点的坐标;(3)、在乙的行驶过程中,当为何值时,甲乙相距千米.25.
(1)、分别求出与之间的函数解析式;(2)、求出点的坐标;(3)、在乙的行驶过程中,当为何值时,甲乙相距千米.25.

 (1)、操作思考:如图1,在平面直角坐标系中,等腰的直角顶点在原点,若顶点A恰好落在点处,则点的坐标为 .(2)、感悟应用:如图2,一次函数的图像与轴交于点A , 与轴交于点 , 过点作线段且 , 直线交轴于点D .
(1)、操作思考:如图1,在平面直角坐标系中,等腰的直角顶点在原点,若顶点A恰好落在点处,则点的坐标为 .(2)、感悟应用:如图2,一次函数的图像与轴交于点A , 与轴交于点 , 过点作线段且 , 直线交轴于点D .①点A的坐标为 , 点B的坐标为;
②直接写出点C的坐标;
(3)、拓展研究:如图3,在平面直角坐标系中,的顶点分别在轴、轴上,且 , , 若点的坐标为 , 点A的坐标为 , 点在第四象限,请求出点的坐标.