湖南省益阳市安化县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列关于的函数是一次函数的是( )A、 B、 C、 D、2. 以下列各数为边长,能构成直角三角形的是( )A、 , , B、 C、 D、3. 下列图象中,表示是的函数的是( )A、
 B、
B、 C、
C、 D、
D、 4. 八年级(1)班共有50名学生,体重最重为72千克,体重最轻为35千克,取组距为10,为统计该班学生的体重情况,可以将该班学生分为( )A、3组 B、4组 C、5组 D、6组5. 已知正比例函数的图象经过第二、四象限,则的取值范围是( )A、 B、 C、 D、6. 已知点和点都在直线的图象上,则与的大小关系为( )A、 B、 C、 D、7. 如图,在四边形中, , , , , 则四边形的面积为( )
4. 八年级(1)班共有50名学生,体重最重为72千克,体重最轻为35千克,取组距为10,为统计该班学生的体重情况,可以将该班学生分为( )A、3组 B、4组 C、5组 D、6组5. 已知正比例函数的图象经过第二、四象限,则的取值范围是( )A、 B、 C、 D、6. 已知点和点都在直线的图象上,则与的大小关系为( )A、 B、 C、 D、7. 如图,在四边形中, , , , , 则四边形的面积为( )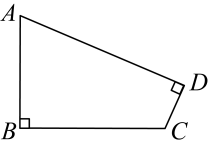 A、48 B、50 C、52 D、548. 如图,在平行四边形中,对角线 , 相交于点 , 交于点 , 连接 , 若的周长为6,则平行四边形的周长为( )
A、48 B、50 C、52 D、548. 如图,在平行四边形中,对角线 , 相交于点 , 交于点 , 连接 , 若的周长为6,则平行四边形的周长为( )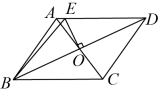 A、8 B、10 C、12 D、149. 如图,以正六边形的一边向内作正方形 , 连接 , 则的度数为( )
A、8 B、10 C、12 D、149. 如图,以正六边形的一边向内作正方形 , 连接 , 则的度数为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,有一只蚂蚁自处向右爬行个单位长度至 , 然后向上爬行个单位长度至处,再向左爬行个单位长度至处,再向下爬行个单位长度至处,再向右爬行个单位长度至处,…,按照此规律继续运动下去,则的坐标为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,有一只蚂蚁自处向右爬行个单位长度至 , 然后向上爬行个单位长度至处,再向左爬行个单位长度至处,再向下爬行个单位长度至处,再向右爬行个单位长度至处,…,按照此规律继续运动下去,则的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若函数是关于的一次函数,则常数的值是 .12. 小明投掷次骰子,并将每次掷出的数字记录下来,结果如下表所示:
次数
数字
则小明掷到数字“”的频率是 .
13. 在平面直角坐标系中,已知点与点关于轴对称,则点的坐标为 .14. 若正多边形的一个内角为 , 则此正多边形为正边形.15. 为了加强我市公民的节能意识,我市制定了如下电费标准:每户每月的用电量不超过200度时,电价为每度元;超过200度时,超过的部分按每度1元收费.现有某户居民5月份用电度,应交电费元,则关于的函数关系式是 .16. 将直线向右平移4个单位长度,则平移后所得的直线的表达式为 .17. 如图,在中, , 平分 , , , 则的长为 .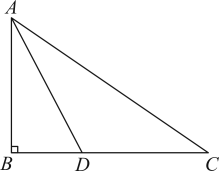 18. 如图,正方形的边长为 , 点在边上,点在上, , 过点作于点 , 交于点 , 若 , 则的长为 .
18. 如图,正方形的边长为 , 点在边上,点在上, , 过点作于点 , 交于点 , 若 , 则的长为 .
三、解答题
-
19. 如图,在中, , , , 于点 . 求的长.
 20. 如图,在四边形中, , 分别是 , 上的中点,且四边形是平行四边形,求证:四边形是平行四边形.
20. 如图,在四边形中, , 分别是 , 上的中点,且四边形是平行四边形,求证:四边形是平行四边形.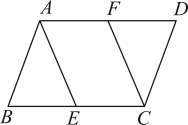 21. 如图,在矩形中,对角线 , 相交于点 , , 分别是 , 的中点.连接 , 若 , , 求矩形的周长.
21. 如图,在矩形中,对角线 , 相交于点 , , 分别是 , 的中点.连接 , 若 , , 求矩形的周长. 22. 暑期将至,某校组织学生进行“防溺水”安全知识竞赛,老师从中随机抽取部分学生的成绩(得分均为整数,满分为100分)进行统计,绘制了如下两幅尚不完整的统计图,根据统计图中的信息解答下列问题:
22. 暑期将至,某校组织学生进行“防溺水”安全知识竞赛,老师从中随机抽取部分学生的成绩(得分均为整数,满分为100分)进行统计,绘制了如下两幅尚不完整的统计图,根据统计图中的信息解答下列问题: (1)、 , .(2)、补全频数分布直方图.(3)、该校共有2000名学生若成绩在90分以上的为优秀,请你估计该校成绩为优秀的学生人数.23. 如图,在平面直角坐标系中,每个小方格的长度为1,已知点 , , .
(1)、 , .(2)、补全频数分布直方图.(3)、该校共有2000名学生若成绩在90分以上的为优秀,请你估计该校成绩为优秀的学生人数.23. 如图,在平面直角坐标系中,每个小方格的长度为1,已知点 , , . (1)、请画出 , 并判断的形状直角三角形.(填“是”或“不是”)(2)、请画出关于轴对称的 .(3)、请画出关于原点对称的 .24. 如图,在平面直角坐标系中,为坐标原点, , 为坐标轴上两点,且 , 连接 .
(1)、请画出 , 并判断的形状直角三角形.(填“是”或“不是”)(2)、请画出关于轴对称的 .(3)、请画出关于原点对称的 .24. 如图,在平面直角坐标系中,为坐标原点, , 为坐标轴上两点,且 , 连接 . (1)、求直线的函数表达式.(2)、直线上是否存在点使得的面积为面积的 , 若存在,求出点的坐标;若不存在,请说明理由.25. 甲、乙两车分别从 , 两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到地停止,乙车行驶到地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为 , 乙车行驶的时间为 , 与之间的函数图象如图所示.
(1)、求直线的函数表达式.(2)、直线上是否存在点使得的面积为面积的 , 若存在,求出点的坐标;若不存在,请说明理由.25. 甲、乙两车分别从 , 两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到地停止,乙车行驶到地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为 , 乙车行驶的时间为 , 与之间的函数图象如图所示. (1)、求甲车行驶的速度.(2)、求的值.(3)、求甲车到达地后与之间的函数表达式.26. 如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)、求甲车行驶的速度.(2)、求的值.(3)、求甲车到达地后与之间的函数表达式.26. 如图1,我们把对角线互相垂直的四边形叫做垂美四边形.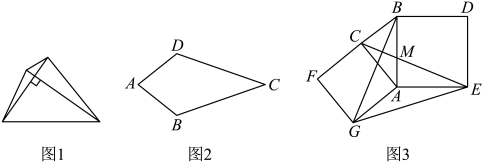 (1)、概念理解:我们已经学习了平行四边形、菱形、矩形、正方形,在这四种图形中是垂美四边形的是 .(2)、性质探究:如图2,已知四边形是垂美四边形,求证: .(3)、问题解决:如图3,分别以的直角边和斜边为边向外作正方形和正方形 , 连接 , , , 交于点 , 已知 , , 求的长.
(1)、概念理解:我们已经学习了平行四边形、菱形、矩形、正方形,在这四种图形中是垂美四边形的是 .(2)、性质探究:如图2,已知四边形是垂美四边形,求证: .(3)、问题解决:如图3,分别以的直角边和斜边为边向外作正方形和正方形 , 连接 , , , 交于点 , 已知 , , 求的长.