湖南省益阳市赫山区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列关于奥运会的剪纸图形中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,下列各点在第四象限的是( )A、 B、 C、 D、3. 下列各曲线中,不表示y是x的函数的是( )A、
2. 在平面直角坐标系中,下列各点在第四象限的是( )A、 B、 C、 D、3. 下列各曲线中,不表示y是x的函数的是( )A、 B、
B、 C、
C、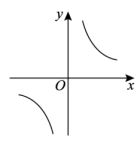 D、
D、 4. 下列函数中,y是x的正比例的函数的是( )A、 B、 C、 D、5. 下面的多边形中,内角和与外角和相等的是( )A、
4. 下列函数中,y是x的正比例的函数的是( )A、 B、 C、 D、5. 下面的多边形中,内角和与外角和相等的是( )A、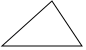 B、
B、 C、
C、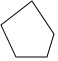 D、
D、 6. 下列在具体情境中不能确定平面内位置的是( )A、东经 , 北纬 B、电影院某放映厅7排3号 C、益阳大道 D、万达广场北偏东方向,2千米处7. 在期末体育考核中,成绩分为优秀、合格、不合格三个档次,某班有40名学生,达到优秀的有18人,合格的有17人,则这次体育考核中,不合格人数的频率是( )A、0.125 B、0.45 C、0.425 D、1.258. 将直线y=2x向下平移3个单位长度后,得到的直线是( )A、y=2x+3 B、y=2x-3 C、y=2(x+3) D、y=2(x-3)9. 如图,在平面直角坐标系xOy中, , B(0,3),P为线段AB的中点,则线段OP的长为( )
6. 下列在具体情境中不能确定平面内位置的是( )A、东经 , 北纬 B、电影院某放映厅7排3号 C、益阳大道 D、万达广场北偏东方向,2千米处7. 在期末体育考核中,成绩分为优秀、合格、不合格三个档次,某班有40名学生,达到优秀的有18人,合格的有17人,则这次体育考核中,不合格人数的频率是( )A、0.125 B、0.45 C、0.425 D、1.258. 将直线y=2x向下平移3个单位长度后,得到的直线是( )A、y=2x+3 B、y=2x-3 C、y=2(x+3) D、y=2(x-3)9. 如图,在平面直角坐标系xOy中, , B(0,3),P为线段AB的中点,则线段OP的长为( ) A、 B、2 C、 D、510. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,问这块沙田面积有多大?题中“里”是我国南宋时期长度单位,则该沙田的面积为( )A、平方里 B、平方里 C、平方里 D、平方里
A、 B、2 C、 D、510. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,问这块沙田面积有多大?题中“里”是我国南宋时期长度单位,则该沙田的面积为( )A、平方里 B、平方里 C、平方里 D、平方里二、填空题
-
11. 如图,在和中, , , 若要用“斜边直角边”直接证明 , 则还需补充条件: .
 12. 函数y= 中自变量x的取值范围是 .13. 如图,在数轴上点A表示的实数是 .
12. 函数y= 中自变量x的取值范围是 .13. 如图,在数轴上点A表示的实数是 . 14. 如果点与点都在直线上,那么mn(填“>”、“<”或“=”).15. 如图,在平行四边形中, , E为上一动点,M , N分别为的中点,则的长为 .
14. 如果点与点都在直线上,那么mn(填“>”、“<”或“=”).15. 如图,在平行四边形中, , E为上一动点,M , N分别为的中点,则的长为 .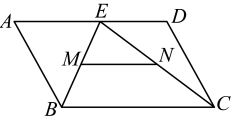 16. 某医院名新生婴儿的体重如下(单位:):
16. 某医院名新生婴儿的体重如下(单位:):为了方便统计,欲制定一张频数统计表,若组距为 , 则应分为6组,其中这一组的频数是 .
17. 已知直线及线段 , 点在直线上,点在直线外.如图.
①在直线上取一点(不与点重合),连接;
②以点为圆心,长为半径作弧,以点为圆心,长为半径作弧,两弧交于点(与点位于直线异侧);
③连接交于点 , 连接 , .
根据以上作图过程及所作图形,在下列结论①;②;③中,一定正确的是(填写所有正确的序号).
18. 如图,在平面直角坐标系中,四边形是矩形,且 , 动点从点出发,以每秒个单位的速度沿线段向点运动,同时动点从点出发,以同样每秒个单位的速度沿折线向点运动,当 , 有一点到达终点时,点 , 同时停止运动.设点 , 运动时间为秒,在运动过程中,如果 , 那么秒.
三、解答题
-
19. 如图,在中, , 点在上,已知 , , . 求的度数.
 20. 如图,在平行四边形中,E,F分别是 , 的中点,求证: .
20. 如图,在平行四边形中,E,F分别是 , 的中点,求证: . 21. 如图,在平面直角坐标系中,是菱形对角线的中点,轴且 , , 将菱形绕点旋转,使点落在轴上,求旋转后点的对应点的坐标.
21. 如图,在平面直角坐标系中,是菱形对角线的中点,轴且 , , 将菱形绕点旋转,使点落在轴上,求旋转后点的对应点的坐标. 22. 阅读下列一段文字:已知在平面内两点P1(x1 , y1),P2(x2 , y2),其两点间的距离P1P2=
22. 阅读下列一段文字:已知在平面内两点P1(x1 , y1),P2(x2 , y2),其两点间的距离P1P2=问题解决:已知A(1,4),B(7,2)
(1)、试求A , B两点的距离;(2)、在x轴上找一点P(不求坐标,画出图形即可),使PA+PB的长度最短,求PA+PB的最短长度.23. 为进一步开展“睡眠管理”工作,某校对部分学生的睡眠情况进行了问卷调查.设每名学生平均每天的睡眠时间为小时,其中的分组情况是:组:;组:;组:;组:;组: , 根据调查结果绘制成两幅完整的统计图,请根据图中提供的信息,解答下列问题: (1)、本次共调查了名学生;(2)、补全条形统计图;(3)、在扇形统计图中,求组所对应的扇形圆心角的度数;(4)、若该校有名学生,请估计该校睡眠时间不足小时的学生有多少人?24. 如图,在中,D是AB上一点, , DE平分∠ADC交AC于点E,DF平分∠BDC交BC于点F, .
(1)、本次共调查了名学生;(2)、补全条形统计图;(3)、在扇形统计图中,求组所对应的扇形圆心角的度数;(4)、若该校有名学生,请估计该校睡眠时间不足小时的学生有多少人?24. 如图,在中,D是AB上一点, , DE平分∠ADC交AC于点E,DF平分∠BDC交BC于点F, . (1)、求证:四边形CEDF是矩形;(2)、若 , , 连接BE,求BE的长.25. 已知一次函数与的图象都经过点 .(1)、求 , 的值;(2)、在同一直角坐标系中画出这两个一次函数的图象,并求出这两个一次函数的图象与轴围成的三角形的面积.(3)、结合函数图象,直接写出当取何值时, .26. 如图1,是线段上的一点,在的同侧作和 , 使 , , , 连接 , 点 , , , 分别是 , , , 的中点,顺次连接 , , , .
(1)、求证:四边形CEDF是矩形;(2)、若 , , 连接BE,求BE的长.25. 已知一次函数与的图象都经过点 .(1)、求 , 的值;(2)、在同一直角坐标系中画出这两个一次函数的图象,并求出这两个一次函数的图象与轴围成的三角形的面积.(3)、结合函数图象,直接写出当取何值时, .26. 如图1,是线段上的一点,在的同侧作和 , 使 , , , 连接 , 点 , , , 分别是 , , , 的中点,顺次连接 , , , .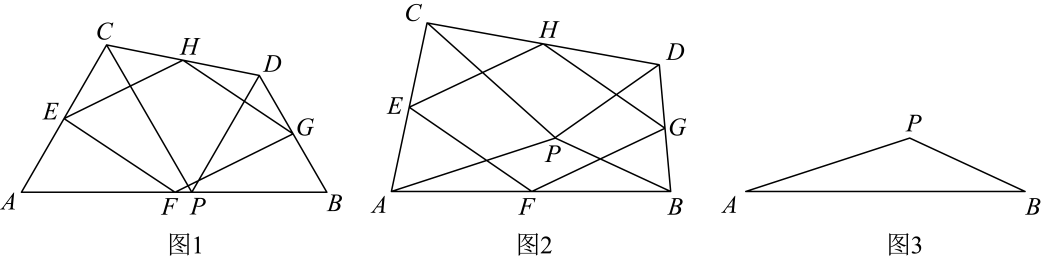 (1)、猜想四边形的形状,直接回答,不必说明理由;(2)、点在线段的上方时,如图2,在的外部作和 , 其他条件不变,(1)中的结论还成立吗?说明理由;(3)、如果(2)中, , 其他条件不变,先补全图3,再判断四边形的形状,并说明理由.
(1)、猜想四边形的形状,直接回答,不必说明理由;(2)、点在线段的上方时,如图2,在的外部作和 , 其他条件不变,(1)中的结论还成立吗?说明理由;(3)、如果(2)中, , 其他条件不变,先补全图3,再判断四边形的形状,并说明理由.