湖南省湘西州吉首市2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 以下各数是最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列各组数据中的三个数作为三角形的边长.其中能构成直角三角形的是( )A、 , 2, B、2,3,4 C、6,7,8 D、1, ,4. 如图,在中,平分交于点E , 若的周长为24, , 则的长为( )
 A、5 B、6 C、7 D、85. 已知点 , 在一次函数的图象上,则m与n的大小关系是( )A、 B、 C、 D、无法确定6. 已知点P(m , n)在第二象限,则直线y=nx+m图象大致是下列的( )A、
A、5 B、6 C、7 D、85. 已知点 , 在一次函数的图象上,则m与n的大小关系是( )A、 B、 C、 D、无法确定6. 已知点P(m , n)在第二象限,则直线y=nx+m图象大致是下列的( )A、 B、
B、 C、
C、 D、
D、 7. 如图,菱形中,对角线、相交于点O , H为边中点,菱形的周长为24,则的长是( )
7. 如图,菱形中,对角线、相交于点O , H为边中点,菱形的周长为24,则的长是( ) A、3 B、 C、 D、128. 下表是某班25名学生右眼视力的检查结果:
A、3 B、 C、 D、128. 下表是某班25名学生右眼视力的检查结果:视力
4.5
4.6
4.7
4.8
4.9
5.0
人数
3
2
4
3
8
5
则这25名学生右眼视力的众数、中位数分别是( ).
A、5.0,4.6 B、4.9,4.7 C、5.0,4.8 D、4.9,4.99. 如图,在中, , , 按以下步骤作图:①以点为圆心,以任意长为半径作弧,分别交 , 于点 , ;②分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 交于点 . 若点到的距离为 , 则的长为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,有函数和的图象,它们相交于点A . 下列结论:
A、 B、 C、 D、10. 如图,在平面直角坐标系中,有函数和的图象,它们相交于点A . 下列结论:①;②;③当时,则有;④关于x的方程的解是:x=2;⑤;⑥ . 其中正确的有( )
 A、①②⑥⑤ B、②③④⑥ C、②③④⑤ D、③④⑤⑥
A、①②⑥⑤ B、②③④⑥ C、②③④⑤ D、③④⑤⑥二、填空题
-
11. 若在实数范围内有意义,则x的取值范围为 .12. 古希腊几何学家海伦通过证明发现:如果一个三角形的三边长分别为.记 , 那么三角形的面积为 , 俗称海伦公式,若在中, , , , 则用海伦公式求得的面积为 .13. 有一架秋千,当它静止时,踏板离地垂直高度 , 将它往前推送水平距离时,秋千踏板离地的垂直高度 , 秋千的绳索始终拉得很直,则绳索长为 .
 14. 已知矩形 , , , 过对角线的中点作的垂直平分线 , 分别交 , 于点 , , 则的长为 .
14. 已知矩形 , , , 过对角线的中点作的垂直平分线 , 分别交 , 于点 , , 则的长为 . 15. 甲、乙两名同学5次立定跳远成绩的平均值都是2.42m,方差分别是: , , 这两名同学成绩比较稳定的是(填“甲”或“乙”).16. 矩形的一条边长是 , 一条对角线的长是4,则这个矩形的面积是 .17. 如图,函数和的图象相交于点A , 则关于x , y的方程组的解为 .
15. 甲、乙两名同学5次立定跳远成绩的平均值都是2.42m,方差分别是: , , 这两名同学成绩比较稳定的是(填“甲”或“乙”).16. 矩形的一条边长是 , 一条对角线的长是4,则这个矩形的面积是 .17. 如图,函数和的图象相交于点A , 则关于x , y的方程组的解为 . 18. 如图,矩形中, , , 是的中点,是线段上一动点,为的中点,连接 , 则线段的最小值为 .
18. 如图,矩形中, , , 是的中点,是线段上一动点,为的中点,连接 , 则线段的最小值为 .
三、解答题
-
19.(1)、计算:;(2)、计算: .20. 如图,在四边形 中, ,对角线 的垂直平分线与边 、 分别相交于M、N.
 (1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的周长.21. 如图,一辆小汽车在一条限速的公路上沿直线行驶,某一时刻刚好行驶到路面车速检测仪的正前方处的点,过了后,测得小汽车所在的点与车速检测仪之间的距离为 .
(1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的周长.21. 如图,一辆小汽车在一条限速的公路上沿直线行驶,某一时刻刚好行驶到路面车速检测仪的正前方处的点,过了后,测得小汽车所在的点与车速检测仪之间的距离为 . (1)、求 , 间的距离;(2)、这辆小汽车超速了吗?请说明理由.22. 如图,在平行四边形中,过点D作于点E,点F在边上, , 连接 .
(1)、求 , 间的距离;(2)、这辆小汽车超速了吗?请说明理由.22. 如图,在平行四边形中,过点D作于点E,点F在边上, , 连接 .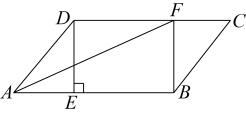 (1)、求证:四边形是矩形;(2)、已知 , 是的平分线,若 , 求的长度.23. 如图,一次函数的图象与轴交于点 , 与正比例函数的图象相交于点 .
(1)、求证:四边形是矩形;(2)、已知 , 是的平分线,若 , 求的长度.23. 如图,一次函数的图象与轴交于点 , 与正比例函数的图象相交于点 . (1)、分别求出这两个函数的解析式;(2)、求的面积;(3)、点在轴上,且是以为腰的等腰三角形,请直接写出点的坐标.24. 为了了解某校初中各年级学生每天的平均睡眠时间(单位:),精确到1h , 抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
(1)、分别求出这两个函数的解析式;(2)、求的面积;(3)、点在轴上,且是以为腰的等腰三角形,请直接写出点的坐标.24. 为了了解某校初中各年级学生每天的平均睡眠时间(单位:),精确到1h , 抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)、求出扇形统计图中百分数的值为 , 所抽查的学生人数为 .(2)、求出平均睡眠时间为8小时的人数,并补全频数分布直方图.(3)、求出这部分学生的平均睡眠时间的众数和平均数.(4)、如果该校共有学生1200名,请你估计睡眠不足(少于)8小时的学生数.25. 端午节是中国四大传统节日之一,有龙舟竞渡、吃粽子、喝雄黄酒的风俗,以此来纪念爱国诗人屈原.端午节期间,某经销商在生产厂家订购了两种畅销的粽子,两种粽子的进货价和销售价如下表:类别价格
种
种
进货价(元/盒)
25
30
销售价(元/盒)
32
40
(1)、若经销商用1500元购进两种粽子,其中种的数量是种数量的2倍少4盒,求两种粽子购进了多少盒;(2)、若经销商计划购进种粽子的数量不少于种粽子数量的2倍,且计划购进两种粽子共60盒,经销商该如何设计进货方案,才能使销售完后获得最大利润?最大利润为多少?26. 如图,直线与轴交于点 , 直线与轴交于点 , 且经过定点 , 直线与交于点 . (1)、求的值;(2)、在轴上是否存在一点 , 使的周长最短?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、求的值;(2)、在轴上是否存在一点 , 使的周长最短?若存在,请求出点的坐标;若不存在,请说明理由.