湖南省怀化市洪江市2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在中, , , 则等于( )A、 B、 C、 D、3. 在平面直角坐标系中,点M(﹣2,1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列函数中,是正比例函数的是( )A、 B、 C、 D、5. 下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是( )A、2,2,3 B、2,3,4 C、3,4,5 D、4,5,66. 如图,在平行四边形中, , 则的度数是( )
2. 在中, , , 则等于( )A、 B、 C、 D、3. 在平面直角坐标系中,点M(﹣2,1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列函数中,是正比例函数的是( )A、 B、 C、 D、5. 下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是( )A、2,2,3 B、2,3,4 C、3,4,5 D、4,5,66. 如图,在平行四边形中, , 则的度数是( )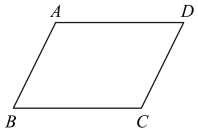 A、 B、 C、 D、7. 如图,学校在小明家的( )方向上.
A、 B、 C、 D、7. 如图,学校在小明家的( )方向上. A、北偏东 B、南偏西 C、北偏东 D、南偏西8. 在四边形中, , 请再添加一个条件,使四边形是矩形,添加的条件不能是( )A、 B、 C、 D、9. 若点 , 在一次函数图象上,比较的大小( )A、 B、 C、 D、无法确定大小10. 一次函数(k为常数,)与正比例函数的图象可能是( )A、
A、北偏东 B、南偏西 C、北偏东 D、南偏西8. 在四边形中, , 请再添加一个条件,使四边形是矩形,添加的条件不能是( )A、 B、 C、 D、9. 若点 , 在一次函数图象上,比较的大小( )A、 B、 C、 D、无法确定大小10. 一次函数(k为常数,)与正比例函数的图象可能是( )A、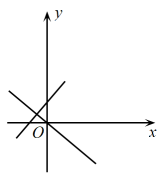 B、
B、 C、
C、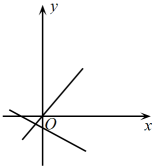 D、
D、
二、填空题
-
11. 若一个多边形的内角和是900º,则这个多边形是边形.12. 在平面直角坐标系中,点关于y轴对称的点的坐标是 .13. 将一次函数的图象向下平移4个单位,得到的一次函数的表达式是 .14. 如图,已知菱形的对角线的长分别为5和8,则这个菱形的面积是 .
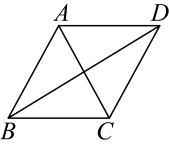 15. 小亮从家匀速跑步到学校,接着马上原路匀速步行回家,已知小亮步行回家的时间是跑步到学校时间的2倍.如图是小亮离家的路程与时间的函数图象,则小亮回家的速度是每分钟步行m.
15. 小亮从家匀速跑步到学校,接着马上原路匀速步行回家,已知小亮步行回家的时间是跑步到学校时间的2倍.如图是小亮离家的路程与时间的函数图象,则小亮回家的速度是每分钟步行m.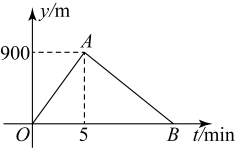 16. 如图,将矩形沿折叠,使顶点C恰好落在边的中点上.若 , , 则的长为 .
16. 如图,将矩形沿折叠,使顶点C恰好落在边的中点上.若 , , 则的长为 .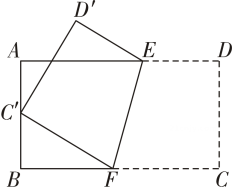
三、解答题
-
17. 如图,已知一次函数(k , b为常数,)的图像经过点 , .
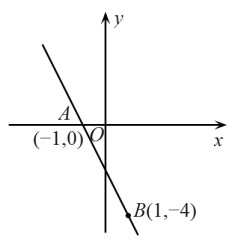 (1)、由图可知,关于x的一元一次方程的解是;(2)、求该一次函数的表达式.18. 已知三个顶点坐标分别为 , , .
(1)、由图可知,关于x的一元一次方程的解是;(2)、求该一次函数的表达式.18. 已知三个顶点坐标分别为 , , .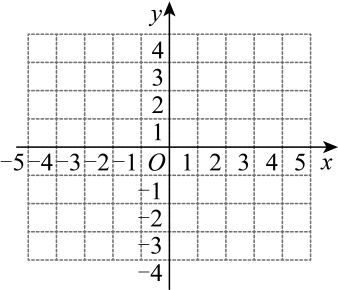 (1)、在平面直角坐标系中画出;(2)、把向左平移6个单位,得到 . 请画出 , 并写出点的坐标.19. 如图,在中, , , 点 , 分别是 , 的中点,连接 , .
(1)、在平面直角坐标系中画出;(2)、把向左平移6个单位,得到 . 请画出 , 并写出点的坐标.19. 如图,在中, , , 点 , 分别是 , 的中点,连接 , .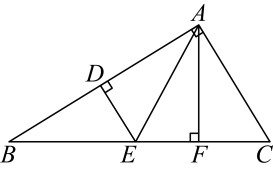 (1)、求证:;(2)、过点作于点 , 求证: .20. 如图,在矩形中,对角线相交于点 , 分别过点作于点 , 于点 , 连接 .
(1)、求证:;(2)、过点作于点 , 求证: .20. 如图,在矩形中,对角线相交于点 , 分别过点作于点 , 于点 , 连接 .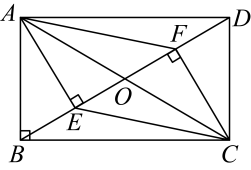 (1)、求证:四边形是平行四边形;(2)、若 , , 求的长.21. 某校八年级举行“每天锻炼一小时,健康生活一辈子”为主题的一分钟跳绳大赛,学校组织了全年级700名学生参加.为了解本次大赛的成绩,八(1)班数学兴趣小组随机抽取了部分学生的成绩作为样本进行统计,制成如图不完整的统计图表,根据所给信息,解答下列问题:
(1)、求证:四边形是平行四边形;(2)、若 , , 求的长.21. 某校八年级举行“每天锻炼一小时,健康生活一辈子”为主题的一分钟跳绳大赛,学校组织了全年级700名学生参加.为了解本次大赛的成绩,八(1)班数学兴趣小组随机抽取了部分学生的成绩作为样本进行统计,制成如图不完整的统计图表,根据所给信息,解答下列问题:成绩x(次/分)
频数(人)
频率
5
5%
a
15%
20
c
b
35%
25
d
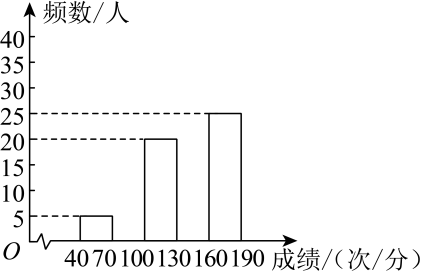 (1)、 , ;(2)、补全频数直方图;(3)、若成绩在130次分以上(包括130次分)为“优良”,请你估计该校八年级参加本次比赛的700名学生中成绩“优良”的有多少人.22. 某商店计划用不超过3400元的资金购买甲、乙两种商品共100个,已知甲、乙商品的进价与售价如下表.设购买甲商品个 , 购买甲商品的费用为元,购买乙商品的费用为元.
(1)、 , ;(2)、补全频数直方图;(3)、若成绩在130次分以上(包括130次分)为“优良”,请你估计该校八年级参加本次比赛的700名学生中成绩“优良”的有多少人.22. 某商店计划用不超过3400元的资金购买甲、乙两种商品共100个,已知甲、乙商品的进价与售价如下表.设购买甲商品个 , 购买甲商品的费用为元,购买乙商品的费用为元.每件商品
进价(元)
售价(元)
甲商品
40
55
乙商品
30
40
(1)、当时, , ;(2)、求最多能购买多少个甲商品;(3)、设全部售出这批甲、乙商品共盈利元,求关于的函数表达式;商店购进多少个甲商品时,才能获得最大利润?最大利润是多少元?23. 如图,以矩形的顶点为原点,以边 , 所在的直线分别为轴,轴建立平面直角坐标系,已知 , . 点在线段上,以每秒1个单位的速度从点向终点运动;点在线段上,以每秒3个单位的速度沿循环运动、连接 . 规定点 , 同时运动,且当点运动到终点时,点同时停止运动,设运动时间为 .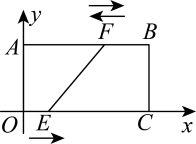 (1)、当点第一次从点向点运动时, . (用含有t的代数式表示)(2)、当点第一次从点返回点时,四边形的面积是10,求出此时的值和点的坐标.(3)、当四边形AOEF恰好是矩形时,求出此时t的值.24. 如图1,在边长为1的正方形中,平分 , 交于点E , 过点E作于点F , 延长交的延长线于点H , 过点F作交于点G , 连接 .
(1)、当点第一次从点向点运动时, . (用含有t的代数式表示)(2)、当点第一次从点返回点时,四边形的面积是10,求出此时的值和点的坐标.(3)、当四边形AOEF恰好是矩形时,求出此时t的值.24. 如图1,在边长为1的正方形中,平分 , 交于点E , 过点E作于点F , 延长交的延长线于点H , 过点F作交于点G , 连接 .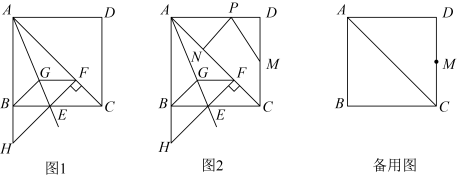 (1)、求证:;(2)、求证:四边形是菱形;(3)、如图2,点M是的中点,点P是上的动点,点N是对角线上的动点,请问是否有最小值?如果有,求出最小值;如果没有,请说明理由.
(1)、求证:;(2)、求证:四边形是菱形;(3)、如图2,点M是的中点,点P是上的动点,点N是对角线上的动点,请问是否有最小值?如果有,求出最小值;如果没有,请说明理由.