湖南省衡阳市衡山县2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 当 $x$ 为任意实数时，下列分式一定有意义的是（）

A、 $\frac{3}{x^{2}}$ B、 $\frac{5}{| x + 6 |}$ C、 $\frac{4}{x^{2} + 1}$ D、 $\frac{2}{x^{2} - 1}$

查看试题解析
2. 2023年1月，中国迎来奥密克戎变异毒株的首波感染高峰．已知该病毒的直径长120纳米，1纳米 $= 1 0^{- 9}$ 米，则这种冠状病毒的直径用科学记数法表示为（）

A、 $1.2 \times 1 0^{- 7}$ 米 B、 $1.2 \times 1 0^{- 11}$ 米 C、 $6 \times 1 0^{- 8}$ 米 D、 $0.6 \times 1 0^{- 7}$ 米

查看试题解析
3. $▱$ ABCD添加下列条件后，仍不能使它成为矩形的是（）

A、AB⊥BC B、AC=BD C、∠A=∠B D、BC= CD

查看试题解析
4. 如图，将函数 $y_{1} = 3 x$ 的图象平移至图中虚线位置，则平移后得到的函数 $y_{2}$ 的解析式为（）

A、 $y_{2} = 3 x + 2$ B、 $y_{2} = 3 x - 2$ C、 $y_{2} = 3 (x + 2)$ D、 $y_{2} = 3 (x - 2)$

查看试题解析
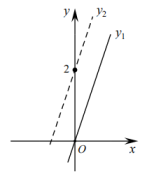5. 在菱形 $A B C D$ 中， $A C = 10$ ， $B C = 13$ ，则该菱形的面积是（）

A、240 B、130 C、120 D、24

查看试题解析
6. 如图，在平面直角坐标系中，平行四边形 $A B C D$ 的顶点 $A$ 、 $B$ 、 $D$ 的坐标分别是 $(0 ， 0)$ 、 $(5 ， 0)$ 、 $(2 ， 3)$ ，则点 $C$ 的坐标是（　　）

A、 $(8 ， 2)$ B、 $(5 ， 3)$ C、 $(7 ， 3)$ D、 $(3 ， 7)$

查看试题解析
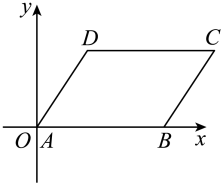7. 对于反比例函数 $y = \frac{6}{x}$ ，下列结论错误的是（）

A、函数图象分布在第一、三象限 B、函数图象经过点 $(- 3 ， - 2)$ C、若点 $(a ， b)$ 在其图象上，那么点 $(- b ， - a)$ 也一定在其图象上 D、若点 $A (x_{1} ， x_{2}) ， B (x_{2} ， y_{2})$ 都在函数图象上，且 $x_{1} < x_{2}$ ，则 $y_{1} > y_{2}$

查看试题解析
8. 如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E．若∠1=35°，则∠2的度数为（）

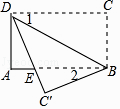A、20° B、30° C、35° D、55°

查看试题解析
9. 一项工程，共有三种施工方案：①甲队单独完成这项工程，刚好如期完工；②乙队单独完成此项工程要比规定工期多用5天；③____，剩下的工程由乙队单独做，也正好如期完工．某同学设规定的工期为x天，根据题意列出了方程： $\frac{4}{x} + \frac{x}{x + 5} = 1$ ，则方案③中被墨水污染的部分应该是（　　）

A、甲乙合作了4天 B、甲先做了4天 C、甲先做了工程的 $\frac{1}{4}$ D、甲乙合作了工程的 $\frac{1}{4}$

查看试题解析
10. 如图， $□ A B C D$ 的对角线 $A C ， B D$ 相交于点O ，下列结论错误的是（）

A、 $S_{▱ A B C D} = 4 S_{△ A O B}$ B、 $O A = O C ， O B = O D$ C、 $A D = B C$ ， $A B / / D C$ D、 $□ A B C D$ 是轴对称图形

查看试题解析
11. 若分式方程 $\frac{x + a}{x - 1} = a$ 无解，则a的值为（）

A、1或 $- 1$ B、 $- 2$ C、1 D、1或 $- 2$

查看试题解析
12. 如图，四边形 $A B C D$ 是菱形， $A C = 8$ ， $D B = 6$ ， $D H ⊥ A B$ 于 $H$ ，则 $D H$ 等于（）

A、 $\frac{12}{5}$ B、 $\frac{6}{5}$ C、 $5$ D、 $\frac{24}{5}$

查看试题解析

二、填空题

13. 计算： $| - 2 | + 3^{- 1} =$ ．

查看试题解析
14. 如图，在平面直角坐标系 $x O y$ 中，正方形 $O A B C$ 的顶点A在x轴上，顶点C在y轴上，且 $O A = 2$ ．若反比例函数 $y = \frac{k}{x}$ 的图象经过点B ，则k的值为．

查看试题解析
15. 写一个y关于x的一次函数，同时满足以下两个条件：
a.图象经过点 $(0 ， 4)$ ；

b.y随x增大而减小，这个函数的表达式可以是．

查看试题解析
16. 若点 $A (a ， b)$ 在反比例函数 $y = - \frac{3}{x}$ 图像上，则代数式 $a b - 1 =$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A B = 5 ， A C = 12 ， B C = 13$ ， P为边 $B C$ 上一动点， $P E ⊥ A B$ 于点E， $P F ⊥ A C$ 于F，则 $E F$ 的最小值为．

查看试题解析
18. 如图，正方形 $A B C D$ 中， $A B = 2$ ， $A C$ ， $B D$ 相交于点O ， E ， F分别为边 $B C$ ， $C D$ 上的动点（点E ， F不与线段 $B C ， C D$ 的端点重合）且 $B E = C F$ ，连接 $O E$ ， $O F$ ， $E F$ ．在点E ， F运动的过程中，有下列四个结论：① $△ O E F$ 是等腰直角三角形；② $△ O E F$ 面积的最小值是 $\frac{1}{2}$ ；③至少存在一个 $△ E C F$ ，使得 $△ E C F$ 的周长是 $2 + \sqrt{3}$ ；④四边形 $O E C F$ 的面积是1．请写出正确结论的序号．

查看试题解析

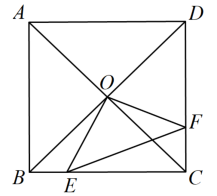
三、解答题

19. 课堂上，李老师给大家出了这样一道题：当 $x = 3$ ， $\frac{2}{5}$ ， $\frac{3}{7}$ 时，求式子 $\frac{x^{2} - 2 x + 1}{x^{2} - 1} \div \frac{2 x - 2}{x + 1}$ 的值．小明一看，“太复杂了，怎么算呢？”你能帮小明解决这个问题吗？请你写出具体过程．

查看试题解析
20. 解分式方程： $\frac{x}{x - 1} - \frac{4}{x^{2} - 1} = 1$ ．

查看试题解析

21. 某校举行了“珍爱生命，预防溺水”主题知识竞赛活动，八（1）、八（2）班各选取五名选手参赛.两班参赛选手成绩依次如下：（单位：分）

八（1）班：8，8，7，8，9

八（2）班：5，9，7， $10$ ， 9

学校根据两班的成绩绘制了如下不完整的统计表：

班级	平均数	众数	中位数
八（1）	8	b	c
八（2）	a	9	9

根据以上信息，请解答下面的问题：

(1)、填空：

a =

，

b =

，

c =

(2)、已知八（1）班比赛成绩的方差是

0.4

，请你计算八（2）班比赛成绩的方差，并从方差的角度分析哪个班级成绩更稳定.

查看试题解析

22. 斑马线前“车让人”，不仅体现着对生命的尊重，也直接反映着城市的文明程度.如图，某路口的斑马线路段 $A - B - C$ 横穿双向行驶车道，其中 $A B = B C = 12$ 米，在绿灯亮时，小林共用11秒通过 $A C$ ，其中通过 $B C$ 段的速度是通过 $A B$ 段速度的1.2倍，求小林通过 $A B$ 段和 $B C$ 段时的速度.

查看试题解析
23. 如图，在平面直角坐标系中，直线 $y = - 2 x + 4$ 与 $y$ 轴、 $x$ 轴分别交于点 $A$ 、 $B$ ，点 $P$ 为直线 $y = - 2 x + 4$ 位于第一象限内一点，已知点 $C (0 ， - 3)$ ．

(1)、求 $A C$ 的长；

(2)、设点 $P$ 的横坐标为 $a$ ．
①直接写出 $a$ 的取值范围为：；

②若 $△ P O B$ 的面积与 $△ P A C$ 的面积相等，求 $a$ 的值．

查看试题解析
24. 如图，点A是菱形 $B D E F$ 对角线的交点， $B C ∥ F D ， C D ∥ B E$ ，连接 $A C$ ，交 $B D$ 于O ．

(1)、求证： $A C = B D$ ；

(2)、若 $B E = 10 ， D F = 24$ ，求 $A C$ 的长．

查看试题解析
25. 学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地．两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示．

(1)、点B的坐标是．

(2)、根据图象信息，甲的速度为米/分钟，当t=分钟时甲乙两人相遇；

(3)、求点A的坐标．

查看试题解析
26. 如图，在边长为 $8$ 的正方形 $A B C D$ 中，点 $E$ 在边 $A B$ 上移动（不与端点重合）．连接 $C E$ ，以 $C E$ 为一边在其右侧作 $△ C E F$ ，其中 $∠ C E F = 90 °$ ， $C E = E F$ ，点 $G$ 为 $F C$ 的中点，过点 $F$ 作 $F H ⊥ A D$ ，垂足为点 $H$ ，连接 $G D$ ， $G H$ ， $F A$ ．

(1)、求证： $∠ E A F = 135 °$ ；

(2)、请判断线段 $G D$ 和 $G H$ 之间有何关系？写出你的结论并证明；

查看试题解析