重庆市涪陵区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列各式中,是最简二次根式的是( )A、 B、 C、 D、2. 若式子有意义,则x的取值范围是( )A、 B、 C、 D、3. 一次函数的图象大致是( )A、
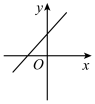 B、
B、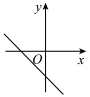 C、
C、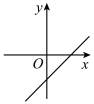 D、
D、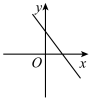 4. 在期末考试中,初二某班级有1组、2组、3组、4组共四个组,每个组学生的数学成绩的平均分相等,方差分别为 , , , , 则该班这四个组的学生期末数学成绩波动最小的是( )A、1组 B、2组 C、3组 D、4组5. 下列四组线段,能构成直角三角形的是( )A、2,2,4 B、 , , 5 C、5,6,7 D、6,8,106. 下列不属于矩形的性质是( )A、两组对边分别平行 B、四个角都相等 C、每一条对角线平分一组内角 D、两条对角线相等7. 小颖家、图书馆、体育馆依次在一条直线上.周六小颖从家出发步行来到图书馆,在图书馆学习了一段时间后,又从图书馆乘车去体育馆锻炼,下面能反映小颖离家的路程y与出发时间x的函数关系的大致图象是( )A、
4. 在期末考试中,初二某班级有1组、2组、3组、4组共四个组,每个组学生的数学成绩的平均分相等,方差分别为 , , , , 则该班这四个组的学生期末数学成绩波动最小的是( )A、1组 B、2组 C、3组 D、4组5. 下列四组线段,能构成直角三角形的是( )A、2,2,4 B、 , , 5 C、5,6,7 D、6,8,106. 下列不属于矩形的性质是( )A、两组对边分别平行 B、四个角都相等 C、每一条对角线平分一组内角 D、两条对角线相等7. 小颖家、图书馆、体育馆依次在一条直线上.周六小颖从家出发步行来到图书馆,在图书馆学习了一段时间后,又从图书馆乘车去体育馆锻炼,下面能反映小颖离家的路程y与出发时间x的函数关系的大致图象是( )A、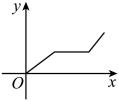 B、
B、 C、
C、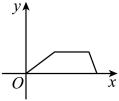 D、
D、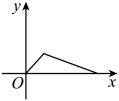 8. 如图,要从电线杆离地面12米处的点N向地面拉一条长为13米的钢缆 , 则地面钢缆固定点A到电线杆底部M的距离是( )米.
8. 如图,要从电线杆离地面12米处的点N向地面拉一条长为13米的钢缆 , 则地面钢缆固定点A到电线杆底部M的距离是( )米.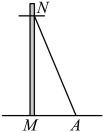 A、3 B、4 C、5 D、69. 如图,矩形的对角线相交于点O,于点E,且 , 若 , 则矩形的面积为( )
A、3 B、4 C、5 D、69. 如图,矩形的对角线相交于点O,于点E,且 , 若 , 则矩形的面积为( )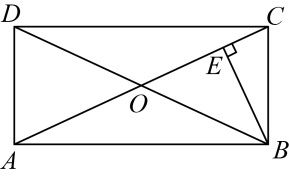 A、12 B、20 C、 D、10. 对于任意实数m,n,若定义新运算 , 给出三个说法:
A、12 B、20 C、 D、10. 对于任意实数m,n,若定义新运算 , 给出三个说法:①;②;③ .
以上说法中正确的个数是( )
A、0个 B、1个 C、2个 D、3个二、填空题
-
11. 化简: .12. 为了了解同学们的睡眠时间,小丽同学了解到班级四位同学某天的睡眠时间分别为7.8小时,8.6小时,8.4小时,8.8小时,则这四位同学该天的平均睡眠时间是小时.13. 若点 , 都在一次函数的图象上,则(用“>”,“<”或“=”填空).14. 在菱形中,对角线交于点O,若菱形的周长为 , , 则菱形的面积是 .
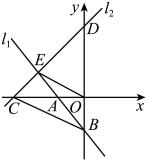
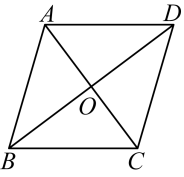 15. 如图,平面直角坐标系中,直线与直线相交于点 , 则不等式的解集为 .
15. 如图,平面直角坐标系中,直线与直线相交于点 , 则不等式的解集为 .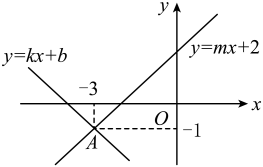 16. 若 , 则代数式的值为 .17. 在矩形中, , , 点M在边上,连接 , 将沿翻折,得到 , 交于点N,若点N为的中点,则的长度为 .
16. 若 , 则代数式的值为 .17. 在矩形中, , , 点M在边上,连接 , 将沿翻折,得到 , 交于点N,若点N为的中点,则的长度为 .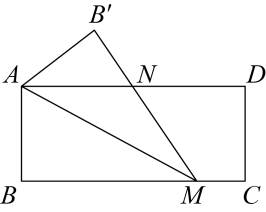 18. 对于一个各位数字都不为零的四位正整数N,若千位数字比十位数字大3,百位数字是个位数字的3倍,那么称这个数N为“三生有幸数”,例如: , ∵ , , ∴5321是个“三生有幸数”;又如 , ∵ , ∴8642不是一个“三生有幸数”.则最小的“三生有幸数”是 . 若将N的千位数字与个位数字互换,百位数字与十位数字互换,得到一个新的四位数,那么称这个新的数为数N的“反序数”,记作 , 例如: , 其“反序数” . 若一个“三生有幸数”N的十位数字为x,个位数字为y,设 , 若除以6余数是1,则所有满足题意的四位正整数N的最大值与最小值的差是 .
18. 对于一个各位数字都不为零的四位正整数N,若千位数字比十位数字大3,百位数字是个位数字的3倍,那么称这个数N为“三生有幸数”,例如: , ∵ , , ∴5321是个“三生有幸数”;又如 , ∵ , ∴8642不是一个“三生有幸数”.则最小的“三生有幸数”是 . 若将N的千位数字与个位数字互换,百位数字与十位数字互换,得到一个新的四位数,那么称这个新的数为数N的“反序数”,记作 , 例如: , 其“反序数” . 若一个“三生有幸数”N的十位数字为x,个位数字为y,设 , 若除以6余数是1,则所有满足题意的四位正整数N的最大值与最小值的差是 .三、解答题
-
19. 计算:(1)、;(2)、 .20. 如图,在平行四边形中 .
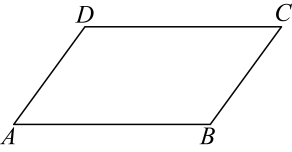 (1)、尺规作图:在边上取一点M,使得 , 连接;作∠ADC的平分线交于点N(保留作图痕迹,不写作法);(2)、在(1)所作图形中,求证:四边形是平行四边形.(请补全下面的证明过程,不写证明理由).
(1)、尺规作图:在边上取一点M,使得 , 连接;作∠ADC的平分线交于点N(保留作图痕迹,不写作法);(2)、在(1)所作图形中,求证:四边形是平行四边形.(请补全下面的证明过程,不写证明理由).证明:∵在平行四边形ABCD中, , ∴ ▲ ,
∵DN平分∠ADC,
∴ ▲ ,
∴ ,
∴ ▲ .
∵在平行四边形ABCD中, ,
又∵ , ∴ ▲ ,
∵在平行四边形ABCD中, ,
∴ , 即 ▲ ,
又∵ , ∴四边形BMDN是平行四边形.
21. 为了激励新时代青年奋发有为、激扬青春,学校团委举行了以“奋进新时代,开启新征程”为主题的征文比赛.现从七年级和八年级参加比赛的学生中各随机抽取20名同学的成绩(百分制)进行分析(单位:分,成绩得分用x表示,成绩均为整数,满分为100分,95分及95分以上为优秀),将学生的比赛成绩分为A,B,C,D四个等级,分别是:A. , B. , C. , D. . 下面给出了部分信息:七年级被抽取的20名学生的比赛成绩分别是:96,84,90,83,87,85,90,96,100,99,98,99,92,93,94,92,89,96,91,86;
八年级被抽取的20名学生的比赛成绩在C等级中的数据分别是:90,91,92,92,93,94;
七、八年级抽取的学生比赛成绩统计表
年级
平均数
中位数
众数
优秀率
七年级
92
92
a
35%
八年级
92
b
98
c%

【小问1】
根据以上信息,解答下列问题:
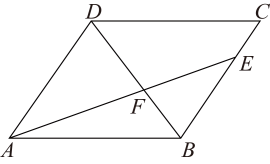
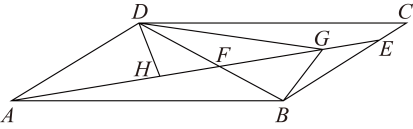
(1)、请填空: , , ;(2)、根据以上数据,你认为这次征文比赛中该校七、八年级中哪个年级学生的成绩更好?请说明理由(一条理由即可);(3)、若该校七年级有1000人、八年级有1200人参加了这次征文比赛活动,请估计七年级、八年级学生参加此次征文比赛成绩为优秀的共有多少人?22. 如图,四边形是菱形,于点E,于点F.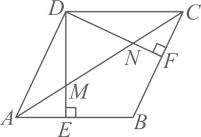 (1)、求证:;(2)、连结 , 分别交于点M,N,求证: .23. 2023年的政府工作报告中传递出文旅发展新动态,某区政府积极响应,对辖区内的景点设施和交通等硬件进行改造和升级,提升消费者的满意程度.如图,该区有A、B、C、D四个景点,景点A、D、C依次在东西方向的一条直线上,景点B在景点D的正北方向、且在景点C的西北方向上,现有公路、、、 , 已知千米,千米.
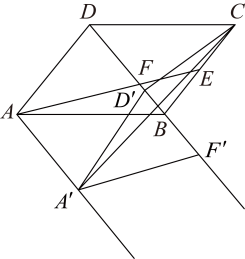
(1)、求证:;(2)、连结 , 分别交于点M,N,求证: .23. 2023年的政府工作报告中传递出文旅发展新动态,某区政府积极响应,对辖区内的景点设施和交通等硬件进行改造和升级,提升消费者的满意程度.如图,该区有A、B、C、D四个景点,景点A、D、C依次在东西方向的一条直线上,景点B在景点D的正北方向、且在景点C的西北方向上,现有公路、、、 , 已知千米,千米.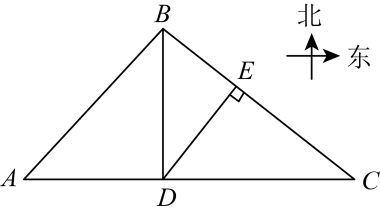 (1)、求公路的长度;(2)、区政府准备在景点C、B之间修一条互通大道(即线段),并在大道上的E处修建一座凉亭方便游客休息,同时D、E之间也修建一条互通大道(即线段),且 . 若修建互通大道、的费用均是每千米100万元,请求出修建互通大道、的总费用约是多少万元?(参考数据: , )24. 如图1,在正方形中, , 动点P从点A出发,沿折线运动,当点P到达点C时停止运动.连结 , 若点P运动的路程为 , 的面积为y,当点P与点B重合时的值为0
(1)、求公路的长度;(2)、区政府准备在景点C、B之间修一条互通大道(即线段),并在大道上的E处修建一座凉亭方便游客休息,同时D、E之间也修建一条互通大道(即线段),且 . 若修建互通大道、的费用均是每千米100万元,请求出修建互通大道、的总费用约是多少万元?(参考数据: , )24. 如图1,在正方形中, , 动点P从点A出发,沿折线运动,当点P到达点C时停止运动.连结 , 若点P运动的路程为 , 的面积为y,当点P与点B重合时的值为0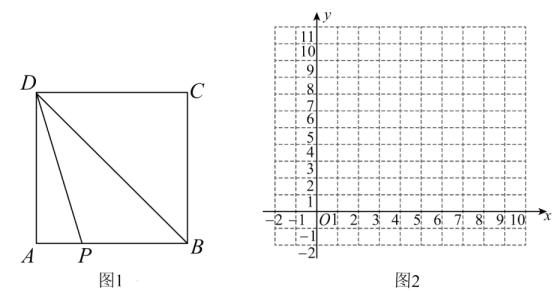 (1)、求y与x之间的函数解析式,并写出自变量x的取值范围;(2)、在图2的平面直角坐标系中画出这个函数的图象,并写出该函数图象的一条性质;(3)、根据图象,直接写出当时,x的取值范围.
(1)、求y与x之间的函数解析式,并写出自变量x的取值范围;(2)、在图2的平面直角坐标系中画出这个函数的图象,并写出该函数图象的一条性质;(3)、根据图象,直接写出当时,x的取值范围.