重庆市秀山土家族苗族自治县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列式子为最简二次根式的是( )A、 B、 C、 D、2. 下列各组数中,能构成直角三角形的是( )A、1,1,2 B、3,4,6 C、7,24,25 D、6,12,133. 经统计甲、乙、丙、丁四个班的同学跳绳成绩的平均数 , , , , 其方差分别为 , , , . 可以出跳绳成绩好且发挥稳定的班级是( )A、甲班 B、乙班 C、丙班 D、丁班4. 估算的值在( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间5. 如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )
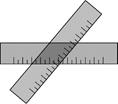 A、矩形 B、菱形 C、正方形 D、无法判断6. 如图,中, , , 于点D,点E为的中点,连接 , 则的长为( )
A、矩形 B、菱形 C、正方形 D、无法判断6. 如图,中, , , 于点D,点E为的中点,连接 , 则的长为( ) A、3 B、4 C、5 D、67. 星期天,小颖从家去体育馆运动,运动结束后按原路返回,下图表示小颖离家距离和时间的关系,下列说法正确的是( )
A、3 B、4 C、5 D、67. 星期天,小颖从家去体育馆运动,运动结束后按原路返回,下图表示小颖离家距离和时间的关系,下列说法正确的是( ) A、小颖家离体育馆 千米 B、小颖在体育馆运动了3小时 C、小颖到家的时间4点钟 D、小颖去时的速度大于回家的速度8. 如图,下列图形是一组按照某种规律摆放而成的图案,则图⑨中圆点的个数是( )
A、小颖家离体育馆 千米 B、小颖在体育馆运动了3小时 C、小颖到家的时间4点钟 D、小颖去时的速度大于回家的速度8. 如图,下列图形是一组按照某种规律摆放而成的图案,则图⑨中圆点的个数是( ) A、81 B、82 C、83 D、849. 如图,正方形边长为20,点P为正方形对角线上任一点,过点P作于点E,作于点F,连接 . 给出以下4个结论:①;②;③的最小值是;④若时,则的长度为 . 其中正确的个数是( )
A、81 B、82 C、83 D、849. 如图,正方形边长为20,点P为正方形对角线上任一点,过点P作于点E,作于点F,连接 . 给出以下4个结论:①;②;③的最小值是;④若时,则的长度为 . 其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个10. 已知整式 , , 则下列说法中正确的有( )
A、1个 B、2个 C、3个 D、4个10. 已知整式 , , 则下列说法中正确的有( )①不存在这样的实数x,使得;②无论x为何值,M和N的值都不可能同时为正;③若a为常数且 , 则;④若 , 则 .
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算: .12. 若一个直角三角形的两直角边长分别是1、2,则第三边长为。13. 已知正比例函数(m为常数),若y随x的增大而增大,则 .14. 已知a、b满足 , 则的值为 .15. 如图,一次函数y1=x+b与一次函数y2=kx+4的图像交于点P (1,3),则关于x的不等式x+b < kx+4的解集是 .
 16. 如图所示,将一张矩形纸片先沿着折叠,使点A刚好落在边上点G处,再沿着折叠(其中点F为上的一点),使点C恰好落在上点H处,连接 , 若 , 且 , 则 .
16. 如图所示,将一张矩形纸片先沿着折叠,使点A刚好落在边上点G处,再沿着折叠(其中点F为上的一点),使点C恰好落在上点H处,连接 , 若 , 且 , 则 . 17. 已知一次函数的图象经过第一、二、三象限,且关于x的分式方程有整数解,则满足条件的所有整数a的和为 .18. 对于一个各数位上的数字均不为0的三位自然数N,若N能被它的各数位上的数字之和m整除,则称N是m的“整倍数”.例如:∵ , ∴135是9的“整倍数”,又如∵∴524不是11的“整倍数”.三位数A是12的“整倍数”,a,b,c分别是数A其中一个数位上的数字,且 . 在a,b,c中任选两个组成两位数,其中最大的两位数记为 , 最小的两位数记为 , 若为整数,求出满足条件的数A的最小值为 .
17. 已知一次函数的图象经过第一、二、三象限,且关于x的分式方程有整数解,则满足条件的所有整数a的和为 .18. 对于一个各数位上的数字均不为0的三位自然数N,若N能被它的各数位上的数字之和m整除,则称N是m的“整倍数”.例如:∵ , ∴135是9的“整倍数”,又如∵∴524不是11的“整倍数”.三位数A是12的“整倍数”,a,b,c分别是数A其中一个数位上的数字,且 . 在a,b,c中任选两个组成两位数,其中最大的两位数记为 , 最小的两位数记为 , 若为整数,求出满足条件的数A的最小值为 .三、解答题
-
19. 化简下列各式.(1)、(2)、20. 如图,已知 , 平分交于点E.
 (1)、使用尺规完成基本作图:作的角平分线,交于点F,交于点G;(保留作图痕迹,不写作法)(2)、在(1)所作图形中,连接 , 求证:四边形是菱形.(请补全下面的证明过程,不写证明理由).
(1)、使用尺规完成基本作图:作的角平分线,交于点F,交于点G;(保留作图痕迹,不写作法)(2)、在(1)所作图形中,连接 , 求证:四边形是菱形.(请补全下面的证明过程,不写证明理由).证明:∵平分 , ∴ ▲ ,
又∵ , ∴ ▲ ,
∴ , ∴ ▲ .
同理可得: ▲ , ∴ .
又∵ ▲ ,
∴四边形是平行四边形,
∵ ,
∴四边形是菱形.
21. 为积极创建“全市儿童青少年近视防控示范学校”,培养学生良好的用眼习惯,某校本学期开展了正确用眼知识竞赛,从中随机抽取20份学生答卷,并统计成绩(成绩得分用x表示,单位:分),收集数据如下:86 82 90 99 98 96 90 100 89 83
87 88 81 90 93 100 96 100 92 100
整理数据:
3
4
a
8
分析数据:
平均数
中位数
众数
92
b
c
请根据以上信息,解答下列问题:
(1)、直接写出上述表格中a,b,c的值;(2)、该校有2700名学生参加了知识竞赛,请估计成绩不低于90分的人数;(3)、请从中位数、众数中选择一个量,结合本题解释它的意义.22. 如图1,已知四边形是平行四边形, , , , 点M从点B出发,沿方向移动到点D停止.过点A作交于点N,设的长为 , 的长为y.请解答下列问题: (1)、写出y与x之间的函数关系式;(2)、通过取点,画图,测量得到了y与x的几组值,如下表:
(1)、写出y与x之间的函数关系式;(2)、通过取点,画图,测量得到了y与x的几组值,如下表:x
4
5
6
7
8
9
y
5
5
a
b
请直接写出a和b的值;
(3)、如图2,请在平面直角坐标系中画出该函数的图象;(4)、请直接写出y的最小值.23. 某儿童玩具商铺售卖甲、乙两种儿童玩具,甲种儿童玩具的销售单价比乙种儿童玩具的销售单价少30元,2件甲种儿童玩具和3件乙种儿童玩具销售总额为740元.(1)、甲种儿童玩具和乙种儿童玩具销售单价分别为多少元?(2)、该儿童玩具商铺店主计划购进甲、乙两种儿童玩具共80件,且甲、乙两种儿童玩具的进价总额不超过8400元,已知甲种儿童玩具每件进价为90元,乙种儿童玩具每件进价为110元,为使甲、乙两种儿童玩具全部售出后总获利最多,请你经过计算分析,给儿童玩具商铺店主提供合理化的进货建议.24. 如图,在平行四边形中,于点E,延长至F点,使 , 连接 . (1)、求证:四边形是矩形;(2)、若 , , , 求的长.25. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点 , 与y轴交于点C,且与正比例函数的图象交于点 .
(1)、求证:四边形是矩形;(2)、若 , , , 求的长.25. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点 , 与y轴交于点C,且与正比例函数的图象交于点 .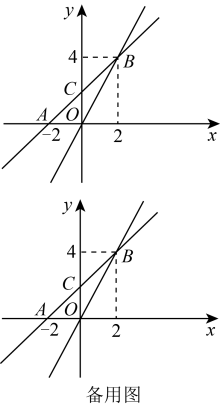 (1)、求一次函数的解析式;(2)、点M在x轴上,当最小时,求点M的坐标;(3)、若D是直线AB上一点,E是平面内一点,以O、C、D、E四点为顶点的四边形是矩形,请直接写出点E的坐标.26. 已知,在平行四边形中,点M是边上一点,连接、 , 且 , 点E是上一动点,连接 .
(1)、求一次函数的解析式;(2)、点M在x轴上,当最小时,求点M的坐标;(3)、若D是直线AB上一点,E是平面内一点,以O、C、D、E四点为顶点的四边形是矩形,请直接写出点E的坐标.26. 已知,在平行四边形中,点M是边上一点,连接、 , 且 , 点E是上一动点,连接 . (1)、如图1,若点E是的中点, , 求平行四边形的面积;(2)、如图2,当时,连接 , 求证:;(3)、如图3,以为直角边作等腰 , , 连接 , 若 , , 当点E在运动过程中,请直接写出周长的最小值.
(1)、如图1,若点E是的中点, , 求平行四边形的面积;(2)、如图2,当时,连接 , 求证:;(3)、如图3,以为直角边作等腰 , , 连接 , 若 , , 当点E在运动过程中,请直接写出周长的最小值.