重庆市永川区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 若函数的图象经过点 , 则的值是( )A、4 B、 C、2 D、3. 下列四组线段中,可以构成直角三角形的是( )A、4,5,6 B、1.5,2,2.5 C、2,3,4 D、1, , 34. 正方形具有而菱形不具有的性质是( )A、对角线相等 B、对角线互相垂直平分 C、四条边相等 D、对角线平分一组对角5. 某校生物小组11人到校外采集标本,其中2人每人采集到6件,4人每人采集到3件,5人每人采集到4件,则这个小组平均每人采集标本( )A、3件 B、4件 C、5件 D、6件6. 若 , 则的值是( )A、0 B、2 C、3 D、2或37. 下列计算错误的是( )A、 B、 C、 D、8. 某班抽取6名同学进行体育达标测试,成绩如下:70,80,65,70,65,70,下列关于对这组数据的描述中,错误的是( )A、中位数是65 B、众数是70 C、平均数是70 D、极差是159. 如图,在平行四边形中,点E,F都在边上,且平分 , 平分 , 若 , , 则边的长是( )
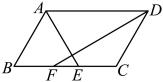 A、3 B、4 C、5 D、610. 如图,直线y=﹣x+2与x轴、y轴分别交于A、B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是( )
A、3 B、4 C、5 D、610. 如图,直线y=﹣x+2与x轴、y轴分别交于A、B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是( )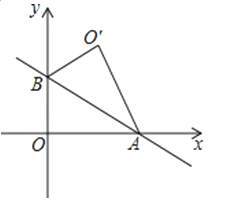 A、( , 3) B、( , ) C、(2,2) D、(2 , 4)
A、( , 3) B、( , ) C、(2,2) D、(2 , 4)二、填空题
-
11. 使有意义的x的取值范围是 .12. 数据6,4,5,3,2的方差是 .13. 如图,在中,O是对角线与的交点, , E是边的中点,连接 , 若的周长是20,则的周长是 .
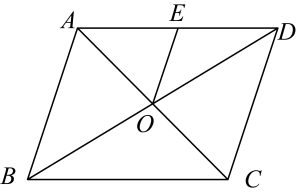 14. 已知函数经过 , 则 .15. 如图,在菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于
14. 已知函数经过 , 则 .15. 如图,在菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于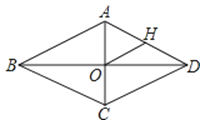 16. 如图所示,已知点A坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为 .
16. 如图所示,已知点A坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为 .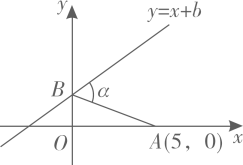 17. 如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为 .
17. 如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为 .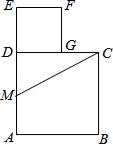 18. 如图,点E是正方形内一点,且 , , 若 , 则正方形的面积是 .
18. 如图,点E是正方形内一点,且 , , 若 , 则正方形的面积是 .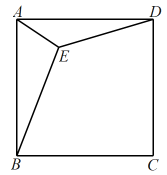
三、解答题
-
19. 计算: .20. 如图,在中, , , 点D在边BC上,且 , , 求BD的长.
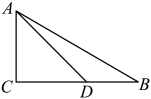 21. 如图,直线是一次函数的图象,直线是一次函数的图象.
21. 如图,直线是一次函数的图象,直线是一次函数的图象.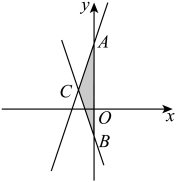 (1)、求、、三点的坐标;(2)、求的面积.22. 为实施“农村留守儿童关爱计划”,某学校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,且有6名留守儿童的班级数占全校班级数的20%,并制成如下不完整的统计图:
(1)、求、、三点的坐标;(2)、求的面积.22. 为实施“农村留守儿童关爱计划”,某学校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,且有6名留守儿童的班级数占全校班级数的20%,并制成如下不完整的统计图: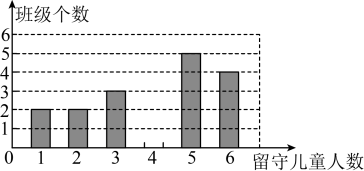 (1)、该校共有多少个班级?并将统计图补充完整;(2)、写出该校各班级留守儿童人数的中位数和众数;(3)、该校平均每班有多少名留守儿童?23. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.
(1)、该校共有多少个班级?并将统计图补充完整;(2)、写出该校各班级留守儿童人数的中位数和众数;(3)、该校平均每班有多少名留守儿童?23. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.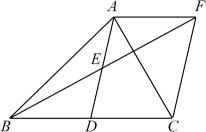 (1)、求证:① △AEF≌△DEB;② 四边形ADCF是平行四边形;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.24. 某天,张强到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有30分钟,于是他立即以(米/分)的速度步行回家取票.在他从体育馆步行回家取票的同时,他父亲骑自行车从家里出发,以(米/分)的速度给他送票,两人在途中相遇,相遇后张强立即坐他父亲的自行车赶回体育馆.下图中线段分别表示父、子俩送票、取票过程中,离体育馆的路程(米)与所用时间(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)、求证:① △AEF≌△DEB;② 四边形ADCF是平行四边形;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.24. 某天,张强到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有30分钟,于是他立即以(米/分)的速度步行回家取票.在他从体育馆步行回家取票的同时,他父亲骑自行车从家里出发,以(米/分)的速度给他送票,两人在途中相遇,相遇后张强立即坐他父亲的自行车赶回体育馆.下图中线段分别表示父、子俩送票、取票过程中,离体育馆的路程(米)与所用时间(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):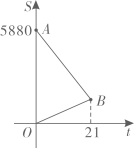 (1)、求的值和点B的坐标;(2)、求直线所表示的函数关系式;(3)、张强能否在比赛开始前到达体育馆?25. 现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.(1)、设A地到甲地运送蔬菜x吨,请完成下表:
(1)、求的值和点B的坐标;(2)、求直线所表示的函数关系式;(3)、张强能否在比赛开始前到达体育馆?25. 现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.(1)、设A地到甲地运送蔬菜x吨,请完成下表:运往甲地(单位:吨)
运往乙地(单位:吨)
A
x
B
(2)、设总运费为W元,请写出W与x的函数关系式(3)、怎样调运蔬菜才能使运费最少?26. 如图,矩形的边、分别在轴和轴上,顶点B在第一象限,点D在的延长线上,已知 , 且 . 把沿矩形的对角线翻折后,顶点A恰好落在线段的中点处.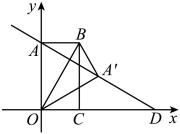 (1)、求的度数;(2)、求线段 , 的长度;(3)、已知点P是直线上的一个动点,在这个坐标平面内是否存在点Q,使得以O、A、P、Q为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由.
(1)、求的度数;(2)、求线段 , 的长度;(3)、已知点P是直线上的一个动点,在这个坐标平面内是否存在点Q,使得以O、A、P、Q为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由.