重庆市长寿区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 化简 $\sqrt{(- 3)^{2}}$ 的结果是（）

A、 $- 3$ B、 $\pm 3$ C、3 D、9

查看试题解析
2. 若 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥1 B、x≤1 C、x＞1 D、x≠1

查看试题解析
3. 若 $△ A B C$ 的三边长为 $a$ ， $b$ ， $c$ ，则下列不是直角三角形的是（）

A、 $a = 6$ ， $b = 7$ ， $c = 8$ B、 $a = 1$ ， $b = \sqrt{3}$ ， $c = \sqrt{2}$ C、 $a = 1.5$ ， $b = 2$ ， $c = 2.5$ D、 $a = 3$ ， $b = 4$ ， $c = 5$

查看试题解析
4. 下列条件中，能判定四边形是平行四边形的是（）

A、一组对边平行 B、对角线互相平分 C、一组对边相等 D、对角线互相垂直

查看试题解析
5. 甲、乙两名同学在5次数学测验中，平均成绩均为95分，这两名同学成绩的方差分别是S_甲²＝0.6，S_乙²＝0.4，则下列说法正确的是（）

A、甲比乙的成绩稳定 B、甲、乙两人的成绩一样稳定 C、乙比甲的成绩稳定 D、无法确定谁的成绩更稳定

查看试题解析
6. 不能判定一个四边形是平行四边形的条件是（）

A、两组对边分别平行 B、一组对边平行，另一组对边相等 C、一组对边平行且相等 D、两组对边分别相等

查看试题解析
7. 一次函数 $y = 3 x - 4$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 如图所示，下列结论中不正确的是（）

A、a组数据的最大数与最小数的差较大 B、a组数据的方差较大 C、b组数据比较稳定 D、b组数据的方差较大

查看试题解析
9. 洗衣机在洗涤衣服时，每浆洗一遍都经历了注水、清洗、排水三个连续过程（工作前洗衣机内无水）．在这三个过程中，洗衣机内的水量y（升）与浆洗一遍的时间x（分）之间函数关系的图象大致为（　　）

A、 B、 C、 D、

查看试题解析
10. 如图，点 $P$ 是正方形 $A B C D$ 的对角线 $B D$ 上一点， $P E ⊥ B C$ ， $P F ⊥ C D$ ，垂足分别为点 $E$ ， $F$ ，连接 $A P$ ， $E F$ ，给出下列四个结论：
① $A P = E F$ ；② $∠ P F E = ∠ B A P$ ；③ $P D = \sqrt{2} E C$ ；④ $△ A P D$ 一定是等腰三角形．其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题

11. 计算： $(\sqrt{50} - \sqrt{8}) \div \sqrt{2} =$ ．

查看试题解析
12. 数据14，10，12，13，11的中位数是

查看试题解析
13. 若 $| a - 2 | + \sqrt{b - 3} + (c - 4)^{2} = 0$ 则 $a - b + c =$ ．

查看试题解析
14. 如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是米．

查看试题解析
15. 如图，矩形 $A B C D$ 的两条对角线相交于点 $O$ ， $∠ A O B = 120 °$ ， $A D = 3$ ，则该矩形对角线的长度等于．

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $A E ⊥ B C$ 于点E，点F在 $A E$ 上， $∠ B A E = ∠ B C F ， F E = B E = 3 A F = 3$ $c m$ ，则 $C F =$ ．

查看试题解析
17. 已知a、b、c是△ABC三边的长，且满足关系式 $\sqrt{c^{2} - a^{2} - b^{2}} + | a - b | = 0$ ，
则△ABC的形状为

查看试题解析
18. 在平面直角坐标系中，等腰直角三角形 $A_{1} B_{1} O$ 、 $A_{2} B_{2} B_{1}$ 、 $A_{3} B_{3} B_{2}$ 、…、 $A_{n} B_{n} {B_{n}}_{－ 1}$ 按如图所示的方式放置，其中点 $A_{1} 、 A_{2} 、 A_{3} 、 \dots 、 A_{n}$ 均在一次函数 $y = k x + b$ 的图象上，点 $B_{1} 、 B_{2} 、 B_{3} 、 \dots 、 B_{n}$ 均在 $x$ 轴上．若点B₁的坐标为 $(1 ， 0)$ ，点 $B_{2}$ 的坐标为 $(3 ， 0)$ ，则点 $A_{8}$ 的坐标为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{27} + \sqrt{\frac{4}{3}} - \sqrt{2} \times \sqrt{6}$ ；

(2)、 $2 \times \sqrt{12} - 6 \times \sqrt{\frac{1}{3}} + \sqrt{6} \div \sqrt{2}$ ．

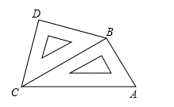
查看试题解析
20. 小明将一副三角板按如图所示摆放在一起，发现只要知道其中一边的长就可以求出其他各边的长，若已知CD=2，求AC的长．

查看试题解析
21. 如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．

(1)、求直线AB的解析式；

(2)、若直线AB上的点C在第一象限，且S_△_BOC=2，求点C的坐标．

查看试题解析
22. 如图，在菱形 $A B C D$ 中， $F$ 为 $A B$ 上一点， $A C$ 与 $D F$ 相交于点 $E$ ．

(1)、求证： $∠ A F E = ∠ E B C$ ；

(2)、如果 $A F = A E$ ，求证： $E C = C B$ ．

查看试题解析
23. 为增强学生体质，国家教育部规定学生每天在校参加体育活动的平均时间不少于1小时（即为达标）．我区为了解学生参加体育活动的基本情况，区人大调查组对部分学校随机抽取了部分学生进行调查，并将调查结果绘制成如下的统计图表（不完整）．请你根据图中提供的信息解答下列问题：
时间（小时）
人数
0.5
60
1.0
a
1.5
40
2.0
总计

(1)、求 $a$ 、 $b$ 的值和抽样学生每天在校体育活动的平均时间；

(2)、求出表示参加体育活动时间为0.5小时的扇形圆心角的度数；

(3)、我区8000名学生参加体育活动时间达标的约有多少人？

查看试题解析
24. 如图，在正方形 $A B C D$ 中，E是 $A B$ 边上任意一点， $B G ⊥ C E$ ，垂足为点O，交 $A C$ 于点F，交 $A D$ 于点G．

(1)、证明： $B E = A G$ ；

(2)、点E位于什么位置时， $∠ A E F = ∠ C E B$ ，说明理由．

查看试题解析
25. 某商业集团新进了40台空调机，60台电冰箱，计划调配给下属的甲、乙两个连锁店销售，其中70台给甲连锁店，30台给乙连锁店．两个连锁店销售这两种电器每台的利润（元）如下表：

空调机
电冰箱
甲连锁店
200
170
乙连锁店
160
150
设集团调配给甲连锁店 $x$ 台空调机，集团卖出这100台电器的总利润为 $y$ （元）．

(1)、求 $y$ 关于 $x$ 的函数关系式，并求出 $x$ 的取值范围；

(2)、为了促销，集团决定仅对甲连锁店的空调机每台让利 $a$ 元销售，其它的销售利润不变，并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润，问该集团应该如何设计调配的方法，使总利润达到最大？最大利润为多少？

查看试题解析
26. 春节期间，某客运站旅客流量不断增大，旅客往往需要很长时间排队等候购票．经调查发现，每天开始售票时，约有 $400$ 人排队购票，同时又有新的旅客不断进入售票厅排队等候购票，售票时售票厅每分钟新增购票人数 $4$ 人，每分钟每个售票窗口出售票数 $3$ 张．每一天售票厅排队等候购票的人数 $y$ （人）与售票时间 $x$ （分钟）的关系如图所示，已知售票的前 $a$ 分钟只开放了两个售票窗口（规定每人只购一张票）．

(1)、求 $a$ 的值．

(2)、求售票到第 $60$ 分钟时售票厅排队等候购票的旅客人数．

(3)、若要在开始售票后半小时内让所有的排队的旅客都能购到票，以便后来到站的旅客随到随购，至少需要同时开放几个售票窗口？

查看试题解析

时间（小时）	人数
0.5	60
1.0	a
1.5	40
2.0
总计

	空调机	电冰箱
甲连锁店	200	170
乙连锁店	160	150