云南省德宏傣族景颇族自治州2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中的无理数是（　　）

A、 $\sqrt{3}$ B、 $- 2$ C、 $0.01001$ D、 $\frac{1}{2}$

查看试题解析
2. 如图， $m ∥ n$ ，其中 $∠ 2 = 140 °$ ，则 $∠ 1$ 的度数为（　　）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
3. 在平面直角坐标系中，点 $P (- 2 ， 1)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 已知 $a < b$ ，下列式子不成立的是（　　）

A、 $- a < - b$ B、 $a + 2 < b + 2$ C、 $a - 1 < b - 1$ D、 $3 a < 3 b$

查看试题解析
5. 下列调查中，最适合采用全面调查的是（　　）

A、调查春节联欢晚会的收视率 B、调查某池塘中现有鱼的情况 C、调查全班同学对排球的喜爱情况 D、了解一批灯泡的使用寿命

查看试题解析
6. 若方程 $a x + 3 y = 2 + 2 x$ 是关于 $x$ ， $y$ 的二元一次方程，则a满足（　　）

A、 $a \neq 0$ B、 $a \neq 1$ C、 $a \neq 2$ D、 $a \neq 3$

查看试题解析
7. 把不等式 $4 x - 2 < 10$ 的解集在数轴上表示出来，正确的是（　　）

A、 B、 C、 D、

查看试题解析
8. 已知 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ 是方程 $m x + y = 5$ 的解，则 $m$ 的值是（　　）

A、 $- 1$ B、 $0$ C、 $5$ D、 $6$

查看试题解析
9. 下列命题中，假命题是（　　）

A、相等的角是对顶角 B、在同一平面内，过一点有且只有一条直线与已知直线垂直 C、在同一平面内，如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条 D、连接直线外一点与直线上各点的所有线段中，垂线段最短

查看试题解析
10. “共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务，成为城市交通出行的新方式，小张对他所在小区居民当月使用“共享单车”的次数进行了抽样调查，并绘制成了如图所示的频数分布直方图（每一组含前一个边界值，不含后一个边界值），则下列说法正确的是（　　）

A、小张一共抽样调查了20人 B、样本中当月使用“共享单车” $50 ~ 60$ 次的人数最多 C、样本中当月使用“共享单车”不足20次的人数有8人 D、样本中当月使用“共享单车”的次数不足30次的人数多于 $50 ~ 60$ 次的人数

查看试题解析
11. 如图，下列条件中能判断 $A D ∥ B C$ 的是（　　）

A、 $∠ 1 = ∠ 4$ B、 $∠ 3 = ∠ 4$ C、 $∠ 1 = ∠ 5$ D、 $∠ D + ∠ B C D = 180 °$

查看试题解析
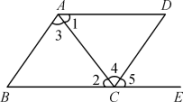12. 若 $x = 2$ 是关于x的一元一次方程 $m x + n = 3$ 的解，则代数式 $6 m + 3 n - 2$ 的值是（　　）

A、2 B、3 C、7 D、9

查看试题解析

二、填空题

13. 比较大小：6 $\sqrt{37}$ （用“＞”或“＜”号填空）．

查看试题解析
14. 空气是由多种气体混合而成的，为了直观地反映空气各成分的百分比，最适合使用的统计图是．

查看试题解析
15. 中国象棋是中华民族的文化瑰宝，因趣味性强，深受大众喜爱．如图，若在象棋棋盘上建立平面直角坐标系，使“兵”位于点 $(- 2 ， 3)$ ， “马”位于点 $(3 ， 0)$ ，那么“炮”在同一坐标系下的坐标是．

查看试题解析
16. 少数民族服饰的花纹和色彩越来越受到追求独立与个性的设计师的喜爱．某民族服饰的花边均是由若干个平移形成的有规律的图案，如图，第①个图案由4个组成，第②个图案由7个组成，第③个图案由10个组成，…，按此规律排列下去，第99个图案中的个数为．

查看试题解析

三、解答题

17. 计算： $\sqrt{16} + \sqrt{3} + \sqrt[3]{- 8} - \sqrt{3} (\sqrt{3} + 1)$

查看试题解析
18. x取哪些正整数时，不等式 $x - 3 (x - 2) \leq 4$ 与 $\frac{1 + 2 x}{3} > x - 1$ 都成立？

查看试题解析
19. 如图，已知 $A (- 5 ， 5) ， B (- 6 ， 1) ， C (- 2 ， 2)$ ，将三角形 $A B C$ 沿 $A D$ 方向平移，点A平移到点D ，点B的对应点为点E ，点C的对应点为点F ，请完成下列问题：

(1)、画出平移后的 $△ D E F$ ；

(2)、分别写出点 $D ， E ， F$ 的坐标．

查看试题解析
20. 如图， $A B ∥ C D$ ，点O在直线 $A B$ 上， $O E$ 平分 $∠ B O D$ ， $∠ A O F = 32 °$ ， $∠ D = 116 °$ ，求 $∠ E O F$ 的度数．

查看试题解析
21. 2022年教育部发布《义务教育劳动课程标准（2022年版）》，劳动将正式成为中小学的一门独立课程．为更好的开展劳动教育，某校想了解学生现阶段每月的劳动时间t（单位：小时），在全校2000名学生中随机抽取部分学生进行了一次问卷调查，并将调查结果分为 $6 ≤ t ＜ 7$ 、 $7 ≤ t ＜ 8$ 、 $8 ≤ t ＜ 9$ 、 $9 ≤ t ＜ 10$ 四个组进行统计，根据统计的信息，绘制了如下图不完整的频数分布直方图、扇形统计图．根据以上信息，解答下列问题：

(1)、请将频数分布直方图补充完整；求 $8 ≤ t ＜ 9$ 对应的圆心角∠1的度数；

(2)、请估计该校2000名学生中每月的劳动时间不少于8小时的人数．

查看试题解析
22. 阅读材料：
我们知道方程组的解与方程组中每个方程的系数和常数项有联系，系数和常数项经过一系列变形、运算就可以求出方程组的解．因此，在现代数学的高等代数学科将系数和常数项排成一个矩阵的形式，规定：关于x ， y的二元一次方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 可以写成矩阵 $(\begin{array}{l} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array})$ 的形式．例如： ${\begin{array}{l} 3 x + 4 y = 16 \\ 5 x - 6 y = 33 \end{array}$ 可以写成矩阵 $(\begin{array}{l} 3 & 4 & 16 \\ 5 & - 6 & 33 \end{array})$ 的形式．

根据以上信息解决下列问题：

(1)、请求出矩阵 $(\begin{array}{l} 4 & 1 & 5 \\ 3 & - 2 & 3 \end{array})$ 对应的方程组的解；

(2)、若矩阵 $(\begin{array}{l} a & - 2 & 3 & 7 \\ 1 & b & 4 & 5 \\ 2 & - 1 & c & 8 \end{array})$ 所对应的方程组的解为 ${\begin{array}{l} x = 1 \\ y = 1 \\ z = 1 \end{array}$ ，求 $a + b + c$ 的值．

查看试题解析
23. 党的二十大报告，深刻阐述了推动绿色发展，促进人与自然和谐共生的理念，尊重自然、顺应自然、保护自然，是全面建设社会主义现代化国家的内在要求．为响应党的号召，某社区欲购进一批树苗进行绿化，已知购进A种树苗80棵，B种树苗30棵，共需要9500元；购进A种树苗50棵，B种树苗60棵，共需要8000元．

(1)、问A ， B两种树苗每棵的进价分别是多少元？

(2)、考虑到绿化效果，购进A种树苗要多于B种树苗，且用于购买这两种树苗的资金不超过7700元，若购进这两种树苗共100棵，则有哪几种购买方案？哪种方案最省钱？最少费用是多少？

查看试题解析
24. 如图，在平面直角坐标系中，已知 $C (b ， a) ， D (0 ， a)$ ，其中a ， b满足 $| a - 2.5 | + (b - 4)^{2} = 0$ ，连接 $A D ， B C ， C D$ ．

(1)、求点C与点D的坐标；

(2)、若 $A C$ 把四边形 $A B C D$ 分成面积相等的两部分，在坐标轴上是否存在一点P ，使 $△ P A C$ 的面积等于四边形 $A B C D$ 的面积，若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析