云南省文山壮族苗族自治州2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 数学考试必备学习用具：黑色的水笔、2B铅笔、橡皮、圆规、三角板全套、量角器．下列学习用具中，不是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 如图是用六块大小相同的小正方体搭建的一个立体几何体，从正面看到的形状是（）

A、 B、 C、 D、

查看试题解析
3. 下列所给线段，能够构成三角形的是（）

A、 $5 c m ， 6 c m ， 10 c m$ B、 $3 c m ， 4 c m ， 8 c m$ C、 $7 c m ， 6 c m ， 13 c m$ D、 $2 c m ， 5 c m ， 2 c m$

查看试题解析
4. 下列计算结果正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 ${(- b^{2})}^{3} = - b^{6}$ C、 $2 x \cdot 2 x = 2 x^{2}$ D、 ${(m - n)}^{2} = m^{2} - n^{2}$

查看试题解析
5. 如图，若直线 $a ∥ b$ ， $∠ 1 = 120 °$ ，则 $∠ 2$ 的度数为（）

A、30° B、40° C、50° D、60°

查看试题解析
6. 如图，从A到B有4条路径，最短的路径是③，理由是（）

A、直线最短 B、两点之间线段最短 C、垂线段最短 D、两点确定一条直线

查看试题解析
7. 如果 $a^{x} = 4$ ， $a^{y} = 9$ ，那么 $a^{x + y}$ 的值为（）

A、13 B、5 C、 $- 36$ D、36

查看试题解析
8. 下列式子中，能用平方差公式进行计算的是（）

A、 $(x + 1) (x - 1)$ B、 $(x + 1) (1 + x)$ C、 $(x + 1) (- x - 1)$ D、 $(x - 1) (1 - x)$

查看试题解析
9. 如图， $△ A B C$ 与 $△ D E F$ 中， $A B = D E$ ， $∠ B = ∠ E$ ，则添加下列条件后，能运用“ $S A S$ ”判断 $△ A B C ≌ △ D E F$ 的是（）

A、 $B C = E F$ B、 $∠ A = ∠ D$ C、 $A C = D F$ D、 $∠ C = ∠ F$

查看试题解析
10. 如图，将水以匀速（即单位时间内注入水的体积相同）注入下面圆柱体的容器中，请找出容器内水的高度h和时间t变化关系的图象（）

A、 B、 C、 D、

查看试题解析
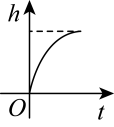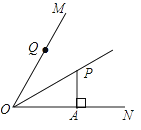
11.
如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=2，则PQ的最小值为（）

A、1 B、2 C、3 D、4

查看试题解析
12. 用棋子摆出下列一组“口”字，按照这种方法摆下去，则第n个“口”字需要用棋子（）

A、（4n﹣4）枚 B、4n枚 C、（4n+4）枚 D、n²枚

查看试题解析

二、填空题

13. - 2023 的相反数是.

查看试题解析
14. 为贯彻落实党的二十大精神，全力推进省委“3815”战略和“强州府”行动，全面奏响驻文企业和州府干部守正创新、干事创业最强音，文山首届“文笔塔杯”篮球友谊赛在盘龙体育馆火力开幕，除VIP区域480张票外，其余普通区域的13000余张票将全部免费赠送，请将13000用科学记数法表示为．

查看试题解析
15. “任意打开七年级数学课本，正好是第35页”，这个事件是事件．（填“随机”或“必然”）

查看试题解析
16. 在直角三角形中，有一个锐角是另外一个锐角的5倍，则这个锐角的度数为度．

查看试题解析

三、解答题

17. 计算： $| - 1 | + {(3.14 - π)}^{0} + {(\frac{1}{3})}^{- 2} + {(- 1)}^{2023}$ ．

查看试题解析
18. 先化简，再求值： $x (x + 2 y) - {(x - 2)}^{2} + 4$ ，其中 $x = 2 ， y = - 1$ ．

查看试题解析
19. 请完成下列证明：如图，已知 $A D ⊥ B C ， E F ⊥ B C ， ∠ 1 = ∠ 2$ ．求证： $D G ∥ B A$ ．

证明：∵ $A D ⊥ B C ， E F ⊥ B C$ （已知）

∴ $∠ E F B = 90 ° ， ∠ A D B =$     ▲    （垂直的定义）

∴ $∠ E F B = ∠ A D B$ （）

∴    ▲ $∥ A D$ （）

∴ $∠ 1 =$     ▲ （）

又∵ $∠ 1 = ∠ 2$ （已知）

∴ $∠ B A D = ∠ 2$ （等量代换）

∴ $D G ∥ B A$ （）

查看试题解析
20. 如图所示，在长度为1个单位长度的小正方形组成的正方形网格中，点A ， B ， C ， D在小正方形的顶点上．

(1)、请画出与四边形 $A B C D$ 关于直线m成轴对称的四边形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ ；

(2)、求四边形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ 的面积；

(3)、在直线m上作一点P ，使得 $P D + P C$ 的长度最小，请在直线m上标出点P的位置．

查看试题解析
21. 让书香浸润人生，让阅读成为习惯，4月21日晚，文山州“深化全民阅读·畅享书香文山”2023年全民阅读大会在文山市民族文化中心举行．文山州某书店借此机会为了吸引更多阅读爱好者，特设立了一个可以自由转动的转盘（如图，转盘被平均分成12份），并规定：顾客每购买100元的图书，就可获得一次转动转盘的机会，如果转盘停止后，指针正好对准红色、黄色、绿色区域（若指针恰好指在分割线上，则重转一次，直到指针指向某一扇形区域为止），那么顾客就可以分别获得50元、30元、20元的购书券，凭购书券可以在书店继续购书．

(1)、甲顾客购书120元，可转动一次转盘，求他获得50元购书券的概率；

(2)、乙顾客购书360元，可获得次转动转盘的机会，求任意转动一次转盘，获得购书券的概率．

查看试题解析
22. 为了进一步贯彻落实“双减”工作，某中学将开展排球、足球兴趣小组活动，体育组王老师购买了排球40个，足球10个，共用了1700元，其中每个排球比每个足球便宜20元．

(1)、求排球、足球的单价各为多少元；

(2)、开展活动后，学校决定再次购买这两种球共70个（每种球的单价不变），王老师做完预算后说：“这两种球共需2490元”，请你用所学的知识解释王老师的预算对不对．

查看试题解析

23. 某公交车每月的支出费用为5000元，每月的乘车人数x（人）与每月利润（利润=收入费用-支出费用）y（元）的变化关系如表所示（每位乘客的公交票价是固定不变的）：

x（人）	500	1000	1500	2000	2500	3000	3500	…
y（元）	$- 4000$	$- 3000$	$- 2000$	$- 1000$	0	1000	2000	…

(1)、观察表中数据可知，每月乘客量达到人及以上时，该公交车才不会亏损；

(2)、根据题意及表中数据关系，写出y与x的关系式；

(3)、如果某月乘车人数为5500人，那么当月的利润是多少元？

查看试题解析

24. 如图．已知线段 $A B$ ，分别过线段 $A B$ 的两个端点作射线 $A M 、 B N$ ，使 $A M ∥ B N$ ，点E为 $∠ M A B$ 平分线上的一点，且 $B E ⊥ A E$ ，垂足为E ，若 $∠ B A E = 60 °$ ，请解答下列问题：

(1)、求 $∠ E B N$ 的度数；

(2)、过点E作直线 $C D$ ，交 $A M$ 于点D ，交 $B N$ 于点C ．求证： $D E = C E$ ；

(3)、无论线段 $D C$ 的两个端点在 $A M 、 B N$ 上如何移动，只要线段 $D C$ 经过点E ，那么 $A D + B C$ 的值是否发生变化？请说明理由．

查看试题解析