云南省文山州2021-2022学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 如图所示,图中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图是用八块相同的小正方体搭建的一个积木,从上面看到的形状是( )
2. 如图是用八块相同的小正方体搭建的一个积木,从上面看到的形状是( ) A、
A、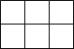 B、
B、 C、
C、 D、
D、 3. 下列各式计算正确的是 ( )A、 B、 C、 D、4. 某冷饮店中的A种可乐比B种可乐每杯贵3元,小霖买了2杯A种可乐、3杯B种可乐,一共花了31元,问A种可乐、B种可乐每杯分别是多少元?若设A种可乐x元,则下列方程中正确的是( )A、 B、 C、 D、5. 下列各选项的事件中,是随机事件的是( )A、的余角是 B、打开电视,正在播放新闻 C、抛掷一枚正方体骰子,出现点数7朝上 D、在中, , 则的形状是锐角三角形6. 等腰三角形的两条边长分别为5和6,则这个等腰三角形的周长是( )A、或 B、 C、 D、或7. 如果是一个完全平方式,那么k的值是( )A、6 B、±6 C、-6 D、±38. 如图,下列条件中,不能判定的是( )
3. 下列各式计算正确的是 ( )A、 B、 C、 D、4. 某冷饮店中的A种可乐比B种可乐每杯贵3元,小霖买了2杯A种可乐、3杯B种可乐,一共花了31元,问A种可乐、B种可乐每杯分别是多少元?若设A种可乐x元,则下列方程中正确的是( )A、 B、 C、 D、5. 下列各选项的事件中,是随机事件的是( )A、的余角是 B、打开电视,正在播放新闻 C、抛掷一枚正方体骰子,出现点数7朝上 D、在中, , 则的形状是锐角三角形6. 等腰三角形的两条边长分别为5和6,则这个等腰三角形的周长是( )A、或 B、 C、 D、或7. 如果是一个完全平方式,那么k的值是( )A、6 B、±6 C、-6 D、±38. 如图,下列条件中,不能判定的是( )
 A、 B、 C、 D、9. 设 , , 则的值是( )A、2 B、8 C、24 D、12810. 如图,现要从幸福小区修建一条连接街道的最短小路,过点作于点 , 沿修建道路就能满足小路最短,这样做的依据是( )
A、 B、 C、 D、9. 设 , , 则的值是( )A、2 B、8 C、24 D、12810. 如图,现要从幸福小区修建一条连接街道的最短小路,过点作于点 , 沿修建道路就能满足小路最短,这样做的依据是( ) A、垂线段最短 B、两点确定一条直线 C、两点之间,线段最短 D、平面内,过一点有且只有一条直线与已知直线垂直11. 若 , 那么代数式M应是( )A、 B、 C、 D、12. 如图,大正方形的边长为a , 小正方形的边长为b , 若用x , y表示四个长方形的两边长(),观察图案及以下关系式:①;②;③;④;⑤ ;其中正确的关系式有 ( )
A、垂线段最短 B、两点确定一条直线 C、两点之间,线段最短 D、平面内,过一点有且只有一条直线与已知直线垂直11. 若 , 那么代数式M应是( )A、 B、 C、 D、12. 如图,大正方形的边长为a , 小正方形的边长为b , 若用x , y表示四个长方形的两边长(),观察图案及以下关系式:①;②;③;④;⑤ ;其中正确的关系式有 ( ) A、①②③④ B、①②③⑤ C、①②④⑤ D、①③④⑤
A、①②③④ B、①②③⑤ C、①②④⑤ D、①③④⑤二、填空题
-
13. —2022的绝对值是.14. 已知一粒米的质量约为克,这个数据用科学记数法表示为克.15. 如图:在中, , 平分 , , , 那么点D到的距离是cm.
 16. 如图,直线c与直线a,b都相交,若 , , 则∠2的度数为.
16. 如图,直线c与直线a,b都相交,若 , , 则∠2的度数为. 17. 如图,已知 , 要用“”说明 , 则需添加的一个条件是 .
17. 如图,已知 , 要用“”说明 , 则需添加的一个条件是 . 18. 杨辉,字谦光,南宋时期杭州人。在他年所著的《详解九章算法》一书中,辑录了如下所示的三角形数表,称之为“开方作法本源”图,并说明此表引自世纪中叶(约公元年)贾宪的《释锁算术》,并绘画了“古法七乘方图”,故此,杨辉三角又被称为“贾宪三角”.请你探索杨辉三角中每一行中所有数字之和的规律,并求出第行中所有数字之和为 .
18. 杨辉,字谦光,南宋时期杭州人。在他年所著的《详解九章算法》一书中,辑录了如下所示的三角形数表,称之为“开方作法本源”图,并说明此表引自世纪中叶(约公元年)贾宪的《释锁算术》,并绘画了“古法七乘方图”,故此,杨辉三角又被称为“贾宪三角”.请你探索杨辉三角中每一行中所有数字之和的规律,并求出第行中所有数字之和为 .
三、解答题
-
19. 先化简,再求值: , 其中 , .20. 某市初级中学在开展“疫情防控,从我做起”的活动中,为了了解该校学生对疫情防控知识的了解程度,现对该校学生进行随机抽样调查,调查结果分为四种:A.非常了解, B.比较了解, C.基本了解, D.不太了解.整理数据并绘制了如下不完整的统计图.

请结合图中所给信息解答下列问题:
(1)、本次共调查了名学生;扇形统计图中,C所对应的扇形的圆心角度数是;(2)、补全条形统计图;(3)、该校共有名学生,根据以上信息,请你估计全校学生对疫情防控知识“非常了解“和“比较了解“的共有多少名?21. 如图,转盘被分成六个相同的扇形,并在上面依次写上数字:2,3,4,5,6,7.指针的位置固定,转动转盘后任其自由停止. (1)、当转盘停止时,指针指向奇数区域的概率是多少?(2)、当转盘停止时,指针指向的数小于或等于5的概率是多少?22. 如图,点A , B , D , E在同一条直线上, , , , 请判断与是否相等?并说明你的理由.
(1)、当转盘停止时,指针指向奇数区域的概率是多少?(2)、当转盘停止时,指针指向的数小于或等于5的概率是多少?22. 如图,点A , B , D , E在同一条直线上, , , , 请判断与是否相等?并说明你的理由. 23. 某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:
23. 某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题: (1)、在这个变化过程中,自变量和因变量分别是什么?(2)、洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?(3)、已知洗衣机的排水速度为每分钟18升,求排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系式.24. 如图,在中 , , 点D是线段上(不与点B、C重合)的动点.
(1)、在这个变化过程中,自变量和因变量分别是什么?(2)、洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?(3)、已知洗衣机的排水速度为每分钟18升,求排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系式.24. 如图,在中 , , 点D是线段上(不与点B、C重合)的动点. (1)、尺规作图:作线段(点E在线段AC上),连接(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 当时,求的度数;(3)、在(1)的条件下,试猜想与的数量关系,并说明理由.
(1)、尺规作图:作线段(点E在线段AC上),连接(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 当时,求的度数;(3)、在(1)的条件下,试猜想与的数量关系,并说明理由.