吉林省四平市双辽市2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{a - 1}$ 有意义，则实数a的取值范围是（）

A、 $a = 1$ B、 $a > 1$ C、 $a < 1$ D、 $a \geq 1$

查看试题解析
2. 矩形，菱形，正方形都具有的性质是（）

A、对角线相等 B、对角线互相平分 C、对角线平分一组对角 D、对角线互相垂直

查看试题解析
3. 下列图形中，不能代表 $y$ 是 $x$ 的函数的是（）．

A、 B、 C、 D、

查看试题解析
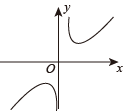4. 下列各点在正比例函数 $y = - 2 x$ 图象上的是（）

A、 $(1 ， - 2)$ B、 $(- 2 ， 1)$ C、 $(4 ， - 2)$ D、 $(\frac{1}{2} ， 1)$

查看试题解析
5. 函数 $y = x - 2$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 数据2，6，4，5，4，3的众数是（）

A、2 B、4 C、5 D、6

查看试题解析

二、填空题

7. 若 $x = \sqrt{5} - 3$ ，则 $\sqrt{x^{2} + 6 x + 9}$ 的值为.

查看试题解析
8. 如图，菱形 $A B C D$ 中， $∠ D ＝ 150 °$ ，则 $∠ C A B$ 的度数为．

查看试题解析
9. 如图，从一个大正方形中裁去两个小正方形，则留下部分的面积为 $c m^{2}$ ．

查看试题解析
10. $1 ~ 6$ 个月的婴儿生长发育非常快，他们的体重 $y$ (克)与月龄 $x$ （月)之间的关系可以用 $y = a + 800 x$ 来近似地表示，其中 $a$ 是婴儿出生时的体重．某个婴儿出生时的体重是3800克，月龄 $x =$ 时体重是7000克．

查看试题解析
11. 如图，一直线与两坐标轴的正半轴分别交于A，B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10，则该直线的函数表达式是．

查看试题解析
12. 函数 $y = 2 x$ 的图像与 $y = 6 - k x$ 如图所示，则k= ．

查看试题解析
13. 若点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 在直线 $y = - 3 x + 2$ 上，且满足 $x_{1} > x_{2}$ ，则 $y_{1}$ $y_{2}$ （选填“>”或“<”）．

查看试题解析
14. 甲、乙两个同学在四次数学模拟测试中，平均成绩都是112分，方差分别是 $S_{甲}^{2} = 5$ ， $S_{乙}^{2} = 12$ ，则甲、乙两个同学的数学成绩比较稳定的是．

查看试题解析
15. 计算： $\sqrt{27}$ + $\sqrt{3}$ － $\sqrt{12}$ =.

查看试题解析

三、解答题

16. 计算： $\sqrt{12} \times \sqrt{3} - \sqrt{12} \div \sqrt{3}$

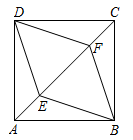
查看试题解析
17. 在直角坐标系中，将直线 $y = - x$ 向下平移2个单位后经过点 $(a ， 2)$ ，求a的值．

查看试题解析
18. 已知：如图，E，F是正方形 $A B C D$ 的对角线 $A C$ 上的两点，且 $C F = A E$ ．求证：四边形 $D E B F$ 是菱形．

查看试题解析
19. 已知，一次函数 $y = - \frac{1}{2} x + 3$ 的图象与 $x$ 轴交于点A ，与y轴交于点B ．

(1)、求A、B两点的坐标；

(2)、画出该函数图象；

(3)、求AB的长．

查看试题解析
20. 在菱形 $A B C D$ 中，两条对角线相交于点O，F是边 $C D$ 的中点，连接 $O F$ 并延长到E，使 $F E = O F$ ，连接 $C E ， D E$ ．

(1)、求证：四边形 $O C E D$ 是矩形；

(2)、求证： $O E ∥ B C$ ．

查看试题解析
21. 已知一次函数 $y = (2 m - 1) x + m + 1$ ．

(1)、若该函数是正比例函数，求这个一次函数的解析式；

(2)、若该函数的图象经过一、二、四象限，且 $m$ 为整数，求这个一次函数的解析式．

查看试题解析
22. 某校开展了全校教师学习党史活动并进行了党史知识竞赛．从七、八年级中各随机抽取了20名教师，统计这部分的竞赛成绩．相关数据统计、整理如下：
抽取的七年级教师的竞赛成绩（单位：分）
6，7，7，8，8，8，8，8，8，8，8，9，9，9，9，10，10，10，10，10．
七八年级教师竞赛成绩统计表
年级
七年级
八年级
平均数
$\bar{x}$
$8.5$
中位数
$a$
9
众数
8
$b$
根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ．

(2)、求所抽取的七年级教师竞赛成绩的平均数 $\bar{x}$ ．

(3)、估计该校七年级120名教师中竞赛成绩达到8分及以上人数．

查看试题解析
23. 如图， $B D$ 是 $△ A B C$ 的角平分线，过点D作 $D E ∥ B C$ 交 $A B$ 于点E， $D F ∥ A B$ 交 $B C$ 于点F．

(1)、求证：四边形 $B E D F$ 为菱形；

(2)、如果 $∠ A = 90 °$ ， $∠ C = 30 °$ ， $B D = 12$ ，求菱形 $B E D F$ 的边长．

查看试题解析
24. 如图，已知函数y₁=2x+b和y₂=ax﹣3的图象交于点P （﹣2，﹣5），这两个函数的图象与x轴分别交于点A、B．

(1)、分别求出这两个函数的解析式；

(2)、求△ABP的面积；

(3)、根据图象直接写出不等式2x+b＜ax﹣3的解集．

查看试题解析
25. 如图，一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．根据图象解决下列问题：

(1)、求慢车和快车的速度；

(2)、求线段 $C D$ 所表示的y与x之间的函数关系式，并写出自变量x的取值范围．

查看试题解析
26. 如图，已知边长为5正方形ABCD中，M、N分别为边BC、DC上的点，连接AM、AN，过N作NH⊥AM于点H，若∠ANH＝45°，连接MN．

(1)、证明：BM＝MN-DN；

(2)、求点A到MN的距离．

查看试题解析

年级	七年级	八年级
平均数	$\bar{x}$	$8.5$
中位数	$a$	9
众数	8	$b$