河北省保定市易县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列函数中,y是x的一次函数的是( )A、 B、 C、 D、2. 若在实数范围内有意义,则的值有可能是( )A、0 B、1 C、2 D、33. 下列各式计算正确的是( )A、 B、 C、 D、4. 在今年“双”来临之际,某品牌鞋专柜为更好的备货,特整理了前期销售这款鞋子尺码的平均数、中位数、众数、方差,其中作为销售主管最关心的数据是( )A、平均数 B、中位数 C、众数 D、方差5. 下列数组不能构成直角三角形三边长的是( )A、3,4,5 B、5,12,13 C、1, , D、2,3,46. 下列选项中,两个变量间的关系不是函数关系的是( )A、直角三角形的两个锐角 B、等腰三角形的底边长与面积 C、圆的周长与半径 D、正方形的周长与边长7. 在中, , , , 则( )A、5 B、 C、3 D、8. 已知点在一次函数的图象上,则与的大小关系是( )A、 B、 C、 D、无法确定9. 如图,在中,是斜边上的中线,若 , 则( )
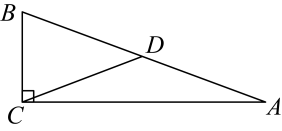 A、 B、 C、 D、10. 已知正比例函数 , 且函数值随自变量的增大而增大,则的取值范围是( )A、 B、 C、 D、无法确定11. 已知且 , 则一次函数的图象大致是( )A、
A、 B、 C、 D、10. 已知正比例函数 , 且函数值随自变量的增大而增大,则的取值范围是( )A、 B、 C、 D、无法确定11. 已知且 , 则一次函数的图象大致是( )A、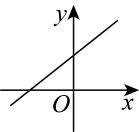 B、
B、 C、
C、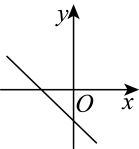 D、
D、 12. 为了解学生参与家务劳动情况,某老师在所任教班级随机调查了10名学生一周做家务劳动的时间,其统计数据如下表:
12. 为了解学生参与家务劳动情况,某老师在所任教班级随机调查了10名学生一周做家务劳动的时间,其统计数据如下表:时间(单位:)
4
3
2
1
0
人数
1
3
3
1
2
则这10名学生一周做家务劳动的平均时间是( )
A、 B、 C、 D、13. 如图,在中, , , 的平分线交边于点 , 则( )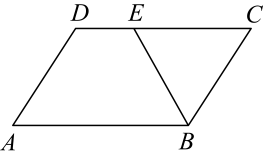 A、10 B、4 C、5 D、214. 现有一矩形 , 借助此矩形作菱形,两位同学提供了如下方案:
A、10 B、4 C、5 D、214. 现有一矩形 , 借助此矩形作菱形,两位同学提供了如下方案:方案I:

取边的中点 , 顺次连接这四点,围成的四边形即为所求.
方案II:
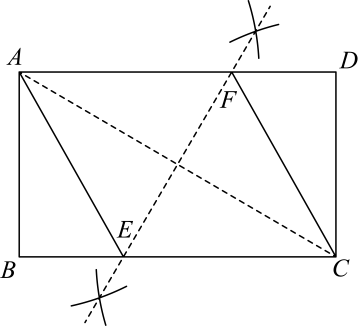
连接 , 作的垂直平分线交于点 , 连接 , 四边形即为所求.
对于方案Ⅰ,Ⅱ,说法正确的是( )
A、I可行、Ⅱ不可行 B、I不可行、Ⅱ可行 C、I、Ⅱ都可行 D、I、Ⅱ都不可行15. 如图,在中,分别是的中点.若 , 四边形的周长是10,则的周长是( )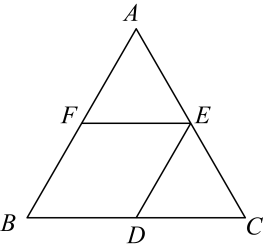 A、15 B、10 C、12.5 D、17.516. 甲、乙两车分别从两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到地停止,乙车行驶到地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为 , 乙车行驶的时间为与之间的函数图象如图所示,下列说法不正确的是( )
A、15 B、10 C、12.5 D、17.516. 甲、乙两车分别从两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到地停止,乙车行驶到地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为 , 乙车行驶的时间为与之间的函数图象如图所示,下列说法不正确的是( )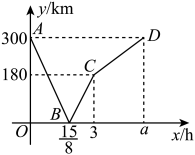 A、甲车行驶的速度为 B、乙车行驶的速度为 C、直线的函数解析式为 D、
A、甲车行驶的速度为 B、乙车行驶的速度为 C、直线的函数解析式为 D、二、填空题
-
17. 甲、乙两名同学5次立定跳远成绩的平均值都是 , 方差分别是 , 这两名同学成绩比较稳定的是(填“甲”或“乙”)18. 如图,每个小正方形的边长为1.
 (1)、三角形是否是直角三角形? . (填“是”或“否”)(2)、边上的高为 .19. 已知是的函数,且 .(1)、若该函数为正比例函数,则 .(2)、将该函数图象向上平移1个单位长度,则新函数图象与x轴交点的横坐标为(用含m的式子表示),将新的函数图象再向右平移2个单位长度,平移后函数图象一定会经过的点的坐标为 .
(1)、三角形是否是直角三角形? . (填“是”或“否”)(2)、边上的高为 .19. 已知是的函数,且 .(1)、若该函数为正比例函数,则 .(2)、将该函数图象向上平移1个单位长度,则新函数图象与x轴交点的横坐标为(用含m的式子表示),将新的函数图象再向右平移2个单位长度,平移后函数图象一定会经过的点的坐标为 .三、解答题
-
20.(1)、 .(2)、 .21. 为了加强对青少年防溺水安全教育,某校开展了“远离溺水,珍爱生命”的防溺水安全知识竞赛.现从七、八年级中随机抽取10名学生的竞赛成绩进行整理、描述和分析(分数用x表示,共分成四组:)
七年级10名学生的成绩:96,86,96,86,99,96,90,100,89,82
八年级10名学生的成绩在C组中的数据:94,90,92
七、八年级抽取的学生竞赛成绩统计表
年级
平均数
中位数
众数
方差
七年级
92
93
38.44
八年级
92
99
34

根据以上信息,解答下列问题:
(1)、 , , .(2)、根据以上数据,你认为在此次防溺水安全知识竞赛中,哪个年级的成绩更好?请说明理由(一条理由即可).22. 如图,一次函数的图象交轴于点 , , 并与一次函数的图象交于点A,点A的横坐标为1.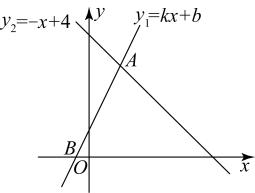 (1)、求一次函数的解析式.(2)、请直接写出时自变量的取值范围.23. 如图,在中, , 动点从点出发,沿射线以的速度移动,设运动的时间为 .
(1)、求一次函数的解析式.(2)、请直接写出时自变量的取值范围.23. 如图,在中, , 动点从点出发,沿射线以的速度移动,设运动的时间为 .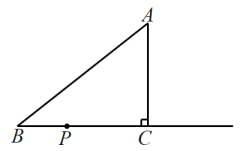 (1)、求边的长.(2)、当时,求的值.24. 如图,在四边形中, , , .
(1)、求边的长.(2)、当时,求的值.24. 如图,在四边形中, , , .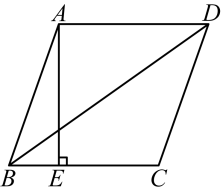 (1)、求证:四边形为菱形.(2)、过点作于点 , 若 , , 求的长.25. 深州蜜桃是河北省特产,已有近两千年的栽培史,古时就有“北国之桃,深州最佳”之说.明清两代,作为“贡桃”送到北京.深州蜜桃有十几个品种,最好的品种有红蜜和白蜜两种,已知甲、乙两果园今年预计蜜桃的产量分别为200吨和300吨,打算成熟后运到 , 两个仓库存放,已知仓库可储存240吨,仓库可储存260吨.甲、乙两果园运往 , 两仓库费用的单价如下表:
(1)、求证:四边形为菱形.(2)、过点作于点 , 若 , , 求的长.25. 深州蜜桃是河北省特产,已有近两千年的栽培史,古时就有“北国之桃,深州最佳”之说.明清两代,作为“贡桃”送到北京.深州蜜桃有十几个品种,最好的品种有红蜜和白蜜两种,已知甲、乙两果园今年预计蜜桃的产量分别为200吨和300吨,打算成熟后运到 , 两个仓库存放,已知仓库可储存240吨,仓库可储存260吨.甲、乙两果园运往 , 两仓库费用的单价如下表:甲果园
乙果园
仓库
150元/吨
140元/吨
仓库
200元/吨
180元/吨
(1)、设甲果园运往仓库的蜜桃吨,求总运费关于的函数解析式及自变量的取值范围.(2)、当甲果园运往仓库多少吨蜜桃时,总运费最少?最少的总运费是多少元?26. 四边形是边长为的正方形,为对角线上一点,连接 . 过点作 , 交于点 . (1)、求证: .(2)、如图2,以为邻边作矩形 , 连接 .
(1)、求证: .(2)、如图2,以为邻边作矩形 , 连接 .①若 , 求的值.
②探究是否存在最大值,若存在,请直接写出这个定值;若不存在,请说明理由.