吉林省长春市二道区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 64的平方根是( )A、32 B、8 C、-8 D、±82. 下列运算正确的是( )A、 B、 C、 D、3. 下列命题:(1)同位角相等,两直线平行;(2)多边形的内角和等于;(3)三角形的外角和等于;(4)平行于同一条直线的两条直线互相平行.其中真命题的个数为( )A、1个 B、2个 C、3个 D、4个4. 若是完全平方式,则k的值是( )A、 B、 C、3 D、65. 在中,的对边分别是a,b,c,下列条件中不能说明 是直角三角形是( )A、 B、 C、 D、6. 如图,已知 , , 欲证 , 不可补充的条件是( )
 A、 B、 C、 D、7. 小明同学在用直尺和圆规作一个角的平分线,具体过程是这样的:
A、 B、 C、 D、7. 小明同学在用直尺和圆规作一个角的平分线,具体过程是这样的:已知: .
求作:的平分线.
作法:第一步:如图,以点为圆心,适当长为半径画弧交于点 , 交于点 .
第二步:分别以点为圆心,大于的长为半径画孤,两弧在的内部相交于点 .
第三步:画射线 .
射线就是所要求作的的平分线.
下列关于小明同学作法的理由,叙述正确的是( )
 A、由可得 , 进而可证 B、由可得 , 进而可证 C、由可得 , 进而可证 D、由“等边对等角”可得8. 如图①,从边长为a的正方形中剪去一个边长为b的小正方形,然后将剩余分剪拼成一个长方形(如图②),则上述操作所能验证的公式是( )
A、由可得 , 进而可证 B、由可得 , 进而可证 C、由可得 , 进而可证 D、由“等边对等角”可得8. 如图①,从边长为a的正方形中剪去一个边长为b的小正方形,然后将剩余分剪拼成一个长方形(如图②),则上述操作所能验证的公式是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 比较大小:3.10. 已知一个立方体的体积是 , 那么这个立方体的棱长是.11. 因式分解:12. 某班级共有名学生,在一次体育抽测中有人不合格,那么不合格人数的频率为 .13. 如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽的工具(卡钳).在图中,若测量得 , 则工件内槽宽 .
 14. 如图,等边中,点是边的中点,的平分线交边于点 , , 点是线段上的任意一点,连接、 , 则的最小值为 .
14. 如图,等边中,点是边的中点,的平分线交边于点 , , 点是线段上的任意一点,连接、 , 则的最小值为 .
三、解答题
-
15. 计算:16. 先化简,再求值: , 其中 .17. 如图,在一张半径为R的圆形钢板上,挖去半径均为r的四个小圆.计算当 , 时剩余部分的面积(取3).
 18. 如图,在中, , , 求和的度数.
18. 如图,在中, , , 求和的度数. 19. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,点、均为格点.只用无刻度的直尺按下列要求在给定的网格中画图,所画图形的顶点均在格点上,不要求写画法.
19. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,点、均为格点.只用无刻度的直尺按下列要求在给定的网格中画图,所画图形的顶点均在格点上,不要求写画法. (1)、在图①中以线段为一腰画一个等腰锐角三角形 .(2)、在图②中以线段为底画一个等腰直角三角形 .(3)、在图③中以线段为边画等腰钝角三角形 .20. 年卡塔尔世界杯足球赛刚刚结束,小明同学随机对身边喜欢足球的同学进行了“我最喜欢的国家球队”问卷调查(问卷共设有五个选项:“—法国”、“—巴西”、“—葡萄牙”、 “—阿根廷”、“—英国”,参加问卷调查的这些学生每人只选其中的一个选项),现将所有的调查结果绘制成如下两幅不完整的统计图:
(1)、在图①中以线段为一腰画一个等腰锐角三角形 .(2)、在图②中以线段为底画一个等腰直角三角形 .(3)、在图③中以线段为边画等腰钝角三角形 .20. 年卡塔尔世界杯足球赛刚刚结束,小明同学随机对身边喜欢足球的同学进行了“我最喜欢的国家球队”问卷调查(问卷共设有五个选项:“—法国”、“—巴西”、“—葡萄牙”、 “—阿根廷”、“—英国”,参加问卷调查的这些学生每人只选其中的一个选项),现将所有的调查结果绘制成如下两幅不完整的统计图:
根据以上信息解决下列问题:
(1)、求本次调查的学生人数.(2)、补全上面的条形统计图.(3)、计算扇形统计图中“”的圆心角度数.21. 如图,在中,是边的中点,过点画直线 , 使 , 交的延长线于点 . (1)、求证:;(2)、若 , , 的长是偶数,则长为 .22. 如图,一架长的梯子斜靠在一竖直的墙上, , 这时,梯子的底端到墙底的距离为 .
(1)、求证:;(2)、若 , , 的长是偶数,则长为 .22. 如图,一架长的梯子斜靠在一竖直的墙上, , 这时,梯子的底端到墙底的距离为 .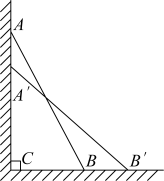 (1)、求此时梯子的顶端距地面的高度 .(2)、如果梯子的顶端沿墙下滑 , 那么梯子底端外移吗?通过计算说明你的结论.23. 阅读材料:
(1)、求此时梯子的顶端距地面的高度 .(2)、如果梯子的顶端沿墙下滑 , 那么梯子底端外移吗?通过计算说明你的结论.23. 阅读材料:若x满足 , 求的值.
解:设 , , 则 ,
∴ ,
∴ .
类比应用:
(1)、若 , 求的值.(2)、若 , 则的值为 .(3)、已知正方形的边长为a,点P和点R分别是边和上的点,且 , , 分别以和为边长作正方形和正方形 . 若图中阴影部分长方形的面积是4,则正方形和正方形的面积和为 .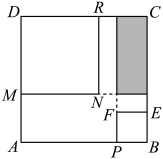 24. 如图,在中, , , , 过点作射线 . 点从点出发,以的速度沿向终点运动:点从点出发,以的速度沿射线运动.点、同时出发,当点到达点时,点、同时停止运动.连结、 , 设运动时间为 .
24. 如图,在中, , , , 过点作射线 . 点从点出发,以的速度沿向终点运动:点从点出发,以的速度沿射线运动.点、同时出发,当点到达点时,点、同时停止运动.连结、 , 设运动时间为 . (1)、线段(用含的代数式表示).(2)、求的长.(3)、当与全等时,
(1)、线段(用含的代数式表示).(2)、求的长.(3)、当与全等时,①若点、的移动速度相同,求的值.
②若点、的移动速度不同,求的值.