吉林省松原市前郭尔罗斯蒙古族自治县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列式子中,是二次根式的是( )A、 B、 C、 D、2. 根据下列条件不能判定三角形是直角三角形的是( )A、 B、 C、 D、3. 菱形具有而矩形不具有的性质是( )A、对边相等 B、对角相等 C、对角线互相平分 D、对角线互相垂直4. 已知点 , 在正比例函数的图象上,且当时,有 , 则的取值范围是( )A、 B、 C、 D、5. 小颖同学参加学校举办的“抗击疫情,你我同行”主题演讲比赛,她的演讲内容、语言表达和形象风度三项得分分别为86分、90分、80分,若这三项依次按照50%,40%,10%的百分比确定成绩,则她的成绩为( )A、84分 B、85分 C、86分 D、87分6. 已知点P(m , n)在第四象限,则直线y=nx+m图象大致是下列的( ).A、
 B、
B、 C、
C、 D、
D、
二、填空题
-
7. 若最简二次根式和能合并,则a的值为.8. 若函数是一次函数,则m的值为.9. 若 , 则等于 .10. 已知一组数据、、、、的平均数是5,则另一组新数组、、、、的平均数是 .11. 如图,在直角三角形ABC和直角三角形ABD中, , , M是AB的中点,连接MC,MD,CD,若 , 则三角形MCD的面积为 .
 12. 如图,某自动感应门的正上方A处装着一个感应器,离地 米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生 正对门,缓慢走到离门1.2米的地方时( 米),感应门自动打开,则 米.
12. 如图,某自动感应门的正上方A处装着一个感应器,离地 米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生 正对门,缓慢走到离门1.2米的地方时( 米),感应门自动打开,则 米.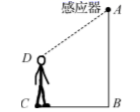 13. 如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 .
13. 如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 .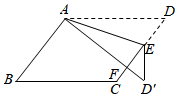 14. 如图,经过点的直线:与直线:相交于点 , 则不等式组的解集为 .
14. 如图,经过点的直线:与直线:相交于点 , 则不等式组的解集为 .
三、解答题
-
15. 计算:16. 已知与成正比,当时, .(1)、求与之间的函数关系式;(2)、当时,求函数的值.17. 如图是一张直角三角形纸片,其中 , , , 现将三角形纸片沿对折,直角边落在上,点C落在点E处,求的面积.
 18. 已知,如图,在平行四边形中,点E、F分别在、的延长线上, , 连接 , 分别交、于G、H.求证: .
18. 已知,如图,在平行四边形中,点E、F分别在、的延长线上, , 连接 , 分别交、于G、H.求证: . 19. 如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
19. 如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
⑴在方格纸中画出以A为直角顶点的直角三角形ABE,点E在小正方形的顶点上,且△ABE的面积为5;
⑵在方格纸中画出以CD为一边的△CDF,点F在小正方形的顶点上,且△CDF的面积为3,CF与(1)中所画线段AE平行,连接BF,请直接写出线段BF的长.
20. 已知 , .(1)、填空: , ;(2)、求的值.21. 如图1,在平面直角坐标系中,直线:过点和 , 与过原点的直线互相垂直,且相交于点 , 为轴上一动点.
 (1)、求直线与直线的函数表达式;(2)、如图 , 当在轴负半轴上运动时,若的面积为 , 求点的坐标;22. 矩形的对角线交于点 , 在边上,连接并延长交边于点 . 若 , , , 求矩形的面积.
(1)、求直线与直线的函数表达式;(2)、如图 , 当在轴负半轴上运动时,若的面积为 , 求点的坐标;22. 矩形的对角线交于点 , 在边上,连接并延长交边于点 . 若 , , , 求矩形的面积. 23. 为了解某校八年级男生在体能测试中引体向上项目的情况,随机抽查了部分男生引体向上项目的测试成绩,绘制如图统计图,请根据相关信息,解答下列问题:
23. 为了解某校八年级男生在体能测试中引体向上项目的情况,随机抽查了部分男生引体向上项目的测试成绩,绘制如图统计图,请根据相关信息,解答下列问题: (1)、本次接受随机抽样调查的男生人数为 , 图①中的值为 ;
(1)、本次接受随机抽样调查的男生人数为 , 图①中的值为 ;本次调查获取的样本数据的平均数为 , 中位数为 .
(2)、若规定引体向上次及以上为该项目良好,根据样本数据,估计该校名男生中该项目良好的人数.(3)、根据良好人数,为了中招体育测试能有更多人得到高分,请你给该校男生提出一些相关建议(最少两条).24. 【阅读理解】我国古人运用各种方法证明勾股定理,如图①,用四个直角三角形拼成正方形,通过证明可得中间也是一个正方形.其中四个直角三角形直角边长分别为a、b,斜边长为c.图中大正方形的面积可表示为(a+b)2 , 也可表示为c2+4×ab,即(a+b)2=c2+4×ab,所以a2+b2=c2 . (1)、【尝试探究】美国第二十任总统伽菲尔德的“总统证法”如图②所示,用两个全等的直角三角形拼成一个直角梯形BCDE,其中△BCA≌△ADE,∠C=∠D=90°,根据拼图证明勾股定理.(2)、【定理应用】在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边长分别为a、b、c.
(1)、【尝试探究】美国第二十任总统伽菲尔德的“总统证法”如图②所示,用两个全等的直角三角形拼成一个直角梯形BCDE,其中△BCA≌△ADE,∠C=∠D=90°,根据拼图证明勾股定理.(2)、【定理应用】在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边长分别为a、b、c.求证:a2c2+a2b2=c4-b4 .
25. 为推进美丽乡村建设,改善人居环境,创建美丽家园.我市甲、乙两工厂积极生产了某种建设物资共800吨,甲工厂的生产量是乙工厂的2倍少100吨,这批建设物资将运往A地420吨,B地380吨,运费如下:(单位:吨)生产厂
A
B
甲
25
20
乙
15
24
(1)、求甲、乙两厂各生产了这批建设物资多少吨?(2)、设这批物资从甲工厂运往A地x吨,全部运往A,B两地的总运费为y元,求y与x之间的函数关系式,写出x的取值范围并设计使总运费最少的调运方案;(3)、由于甲工厂到A地的路况得到了改善,缩短了运输距离和运输时间,运费每吨降低m元(0<m≤15),其余路线运费不变.若到A,B两市的总运费的最小值不小于14020元,求m的取值范围.26. 如图,在平面直角坐标系中,O是坐标原点,正方形的顶点A、C分别在x轴与y轴上,已知正方形边长为3,点D为x轴上一点,其坐标为 , 连接 , 点P从点C出发以每秒1个单位的速度沿折线的方向向终点A运动,当点P与点A重合时停止运动,运动时间为t秒. (1)、连接 , 当点P在线段上运动,且满足时,求直线的表达式;(2)、连接 , 求的面积S关于t的函数表达式;(3)、点P在运动过程中,是否存在某个位置使得为等腰三角形,若存在,直接写出点P的坐标,若不存在,说明理由.
(1)、连接 , 当点P在线段上运动,且满足时,求直线的表达式;(2)、连接 , 求的面积S关于t的函数表达式;(3)、点P在运动过程中,是否存在某个位置使得为等腰三角形,若存在,直接写出点P的坐标,若不存在,说明理由.