吉林省长春市榆树市2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{3 x}{5 - x}$ 有意义，则x的取值范围是（）

A、 $x \neq 0$ B、 $x \neq - 5$ C、 $x \neq 5$ D、 $x > 5$

查看试题解析
2. 斑叶兰的种子小得简直像灰尘一样，1亿粒斑叶兰种子才50克重，因种子太小，只有放在显微镜下才能看清它的真面目，它的一粒种子重约0.0000005克，数据0.0000005用科学记数法表示为（）

A、 $0.5 \times 1 0^{- 7}$ B、 $5 \times 1 0^{- 8}$ C、 $5 \times 1 0^{7}$ D、 $5 \times 1 0^{- 7}$

查看试题解析
3. 若反比例函数 $y = \frac{k}{x}$ 的图象经过点（3，-5），则该反比例函数的图象位于（）

A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限

查看试题解析
4. 在端午节到来之前，儿童福利院对全体小朋友爱吃哪几种粽子作调查，以决定最终买哪种粽子．下面的调查数据中最值得关注的是（）

A、方差 B、平均数 C、中位数 D、众数

查看试题解析
5. 若将直线 $y = x - 3$ 向上平移2个单位，则平移后得到的直线与y轴的交点坐标为（）

A、（0，2） B、（0，－5） C、（1，0） D、（0，－1）

查看试题解析
6. 函数y＝－3x＋1图象上有两点A（1，y₁），B（3，y₂），则y₁与y₂的大小关系是（）

A、y₁＞y₂ B、y₁＜y₂ C、y₁＝y₂ D、无法确定

查看试题解析
7. 如图，四边形ABCD的对角线AC、BD相交于点O，下列判断正确的是（）

A、若 $A C ⊥ B D$ ，则四边形ABCD是菱形 B、若 $A C = B D$ ，则四边形ABCD是矩形 C、若 $A C ⊥ B D$ ， $A C = B D$ ，则四边形ABCD是正方形 D、若 $A O = O C$ ， $B O = O D$ ，则四边形ABCD是平行四边形

查看试题解析
8. 如图，A、B是函数 $y = \frac{2}{x}$ 的图像上关于原点对称的任意两点， $B C / / x$ 轴， $A C / / y$ 轴， $△ A B C$ 的面积记为S，则（）

A、 $S = 2$ B、 $S = 4$ C、 $2 < S < 4$ D、 $S > 4$

查看试题解析

二、填空题

9. 计算： $(- \frac{3}{2})^{- 1}$ = ．

查看试题解析
10. 某运动队要从甲、乙、丙三名跳高运动员中选拔一人参加比赛，教练组统计了最近几次队内选拔赛的成绩并进行了分析，得到下表：

甲
乙
丙
平均数（cm）
176
173
176
方差（ $c m^{2}$ ）
10.5
10.5
42.1
根据表中数据，教练组应该选择参加比赛（填“甲”或“乙”或“丙”）

查看试题解析
11. 如图，在□ABCD中，BE平分∠ABC交AD于点E．若AB=4，BC=7，则DE的长为．

查看试题解析
12. 如图，已知直线y＝ax+b和直线y＝kx交于点P ，若二元一次方程组 ${\begin{matrix} y = k x \\ y = a x + b \end{matrix}$ 的解为x、y ，则关于x+y＝．

查看试题解析
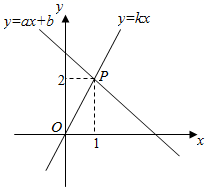13. 如图，E是▱ABCD内任意一点，连接AE、BE、CE、DE．若▱ABCD的面积是10，则阴影部分图形的面积是．

查看试题解析
14. 如图，矩形ABCD中，AB＝5，AD＝3，点M在边CD上，若MA平分∠DMB，则DM的长是．

查看试题解析

三、解答题

15. 先化简，再求值： $\frac{a + 1}{a} \div (a - \frac{1}{a})$ ，其中a＝2023．

查看试题解析
16. 图①、图②、图③均是5×5的正方形网格，每个小正方形的顶点称为格点，点A、B均在格点上．只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上且不全等．
图①图②图③

(1)、在图①中画一个正方形ACBD．

(2)、在图②中画一个平行四边形AEBF．

(3)、在图③中画一个菱形AMBN．

查看试题解析
17. 甲、乙两公司各为希望工程捐款20000元，已知乙公司比甲公司人均多捐20元，且乙公司的人数是甲公司人数的 $\frac{4}{5}$ ，问甲、乙两公司人均捐款各为多少元．

查看试题解析
18. 如图，正比例函数 $y = 2 x$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象有一个交点为 $P (2 ， m)$ .

(1)、求反比例函数 $y = \frac{k}{x}$ 函数表达式；

(2)、根据图象，直接写出当 $- 4 < x < - 1$ 时， $y$ 的取值范围.

查看试题解析
19. 已知：如图，ABCD中，E、F分别是AC上两点，且BE⊥AC于E，DF⊥AC于F．求证：四边形BEDF是平行四边形．

查看试题解析
20. 某校为了改善学生伙食，准备午餐为学生提供鸡腿．现有A、B两家副食品厂可以提供规格为 $75 g$ 的鸡腿，而且它们的价格相同，品质也相近．质检人员分别从两家随机各抽取10个，记录它们的质量（单位：g）如下：
A加工厂 74 74 74 75 73 77 78 72 76 77
B加工厂 78 74 77 73 75 75 74 74 75 75
并对以上数据进行整理如下：

平均数
中位数
众数
方差
A加工厂
75
74.5
b
3.4
B加工厂
75
a
75
2
根据以上分析，回答下列问题：

(1)、统计表中a= ， b=；

(2)、根据以上信息估计B加工厂加工的100个鸡腿中，质量为 $75 g$ 的鸡腿有多少个？

(3)、如果考虑鸡腿的规格，学校应该选购哪家加工厂的鸡腿？说明理由．

查看试题解析
21. 如图，在△ABC中，AB＝CB，BD平分∠ABC交AC于点D，点E在线段BD上，点F在BD的延长线上，且DE＝DF，顺次连接A、E、C、F．

(1)、求证：四边形AECF是菱形．

(2)、若EF＝2，AC＝4，直接写出四边形AECF的周长．

查看试题解析
22. “绿色出行，低碳环保”，共享电动车是一种新理念下的交通工具，现有甲、乙两种品牌的共享电动车，收费标准y（元）与骑行时间x（分）之间的函数关系如图所示，请根据图象信息，解答下列问题：

(1)、甲品牌共享电动车每分钟收费元．

(2)、当骑行时间不低于10分钟时，求乙品牌共享电动车y与x之间的函数关系式．

(3)、已知两种品牌共享电动车的平均行驶速度均为 $20 k m / h$ ，若小明需要骑行共享电动车去上班，小明家到单位的距离为 $6 k m$ ，请通过计算帮小明选择哪个品牌的共享电动车更省钱．

查看试题解析
23. 将边长为2的正方形纸片 $A B C D$ 按如下操作：

(1)、【操作一】如图①，将正方形纸片 $A B C D$ 对折，使点A与点B重合，点D与点C重合，再将正方形纸片 $A B C D$ 展开，得到折痕EF．则点B、点F之间的距离为．

(2)、【操作二】如图②，G为正方形 $A B C D$ 边 $B C$ 上一点，连接 $A G$ ，将图①的正方形纸片沿 $A G$ 翻折，使点B的对称点H落在折痕 $E F$ 上．连接 $B H$ ．
　
①求证： $△ A B H$ 是等边三角形．
②求四边形 $C F G H$ 的周长．

查看试题解析
24. 如图，在矩形 $A B C D$ 中， $A B = 4 ， B C = 5$ ，延长 $B C$ 到点E，使 $C E = 3$ ，连接 $D E$ ．动点P从点B出发，以每秒2个单位的速度沿折线 $B C – C D$ 向终点D运动，设点P运动的时间为t秒．（t＞0）

(1)、 $D E =$ ．

(2)、连结 $A P$ ，当四边形 $A P E D$ 是菱形时，求菱形 $A P E D$ 的周长．

(3)、连结 $B P 、 P D$ ，设四边形 $A B P D$ 的面积为S，求S与t之间的函数关系式．

查看试题解析

	甲	乙	丙
平均数（cm）	176	173	176
方差（ $c m^{2}$ ）	10.5	10.5	42.1

	平均数	中位数	众数	方差
A加工厂	75	74.5	b	3.4
B加工厂	75	a	75	2