山东省德州市庆云县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
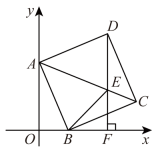
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 已知是一次函数,则m的值为( )A、1 B、2 C、 D、3. 下列各组数据中,不能作为直角三角形边长的是 ( )A、3,4,5 B、5, , C、3,5,7 D、1,2,4. , 是正比例函数的图象上的两个点,则 , 的大小关系是( )A、 B、 C、 D、不能确定5. 如图,四边形的对角线 , 相交于点O, , 且 , 则添加下列一个条件能判定四边形是菱形的是( )
 A、 B、 C、 D、6. 甲、乙两种物质的溶解度(g)与温度t()之间的对应关系如图所示,则下列说法中,错误的是( )
A、 B、 C、 D、6. 甲、乙两种物质的溶解度(g)与温度t()之间的对应关系如图所示,则下列说法中,错误的是( ) A、甲、乙两种物质的溶解度均随温度升高而增大 B、30时两种物质的溶解度一样 C、0时两种物质的溶解度相差10g D、在0-40之间,甲的溶解度比乙的溶解度高7. 如图,有一根电线杆在离地面处的A点断裂,此时电线杆顶部C点落在离电线杆底部B点远的地方,则此电线杆原来长度为( )
A、甲、乙两种物质的溶解度均随温度升高而增大 B、30时两种物质的溶解度一样 C、0时两种物质的溶解度相差10g D、在0-40之间,甲的溶解度比乙的溶解度高7. 如图,有一根电线杆在离地面处的A点断裂,此时电线杆顶部C点落在离电线杆底部B点远的地方,则此电线杆原来长度为( )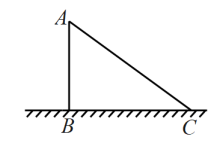 A、 B、 C、 D、8. 小明用四根长度相同的木条制作了如图1所示的能够活动的菱形学具,并测得 , 对角线 , 接着把活动学具变为图2所示的正方形,则图2中的对角线的长为( )
A、 B、 C、 D、8. 小明用四根长度相同的木条制作了如图1所示的能够活动的菱形学具,并测得 , 对角线 , 接着把活动学具变为图2所示的正方形,则图2中的对角线的长为( ) A、 B、 C、 D、9. 某中学举办了以“放歌新时代奋进新征程”为主题的知识竞答比赛(共10道题,每题1分).已知选取了10名学生的成绩,且10名学生成绩的中位数和众数相同,但在记录时遗漏了一名学生的成绩.如图是参赛9名学生的成绩,则这10名学生成绩的中位数是( )
A、 B、 C、 D、9. 某中学举办了以“放歌新时代奋进新征程”为主题的知识竞答比赛(共10道题,每题1分).已知选取了10名学生的成绩,且10名学生成绩的中位数和众数相同,但在记录时遗漏了一名学生的成绩.如图是参赛9名学生的成绩,则这10名学生成绩的中位数是( ) A、7 B、7.5 C、8 D、910. 如图,直线l是一次函数的图象,且直线l过点 , 则下列结论错误的是( )
A、7 B、7.5 C、8 D、910. 如图,直线l是一次函数的图象,且直线l过点 , 则下列结论错误的是( )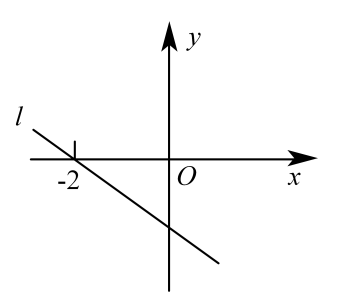 A、 B、直线l过坐标为的点 C、若点 , 在直线上,则 D、11. “勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边为边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为( )
A、 B、直线l过坐标为的点 C、若点 , 在直线上,则 D、11. “勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边为边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为( ) A、126 B、127 C、128 D、12912. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )
A、126 B、127 C、128 D、12912. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )①;②;③;④;⑤
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
13. 代数式在实数范围内有意义,则实数x的取值范围是 .14. 如图,为了测量池塘两岸A,B两点之间的距离,可在外选一点C,连接和 , 再分别取、的中点D,E,连接并测量出的长,即可确定A、B之间的距离.若量得 , 则A、B之间的距离为m
 15. 如图,一个梯子斜靠在一竖直的墙上,测得 , 若梯子的顶端沿墙下滑 , 这时梯子的底端也向右滑 , 则梯子的长度为.
15. 如图,一个梯子斜靠在一竖直的墙上,测得 , 若梯子的顶端沿墙下滑 , 这时梯子的底端也向右滑 , 则梯子的长度为. 16. 如图,直线:分别与 , 轴交于、B两点,过点B的直线交x轴的负半轴于点C,且 , 直线的函数解析式为 .
16. 如图,直线:分别与 , 轴交于、B两点,过点B的直线交x轴的负半轴于点C,且 , 直线的函数解析式为 . 17. 如图1,中,点P从A点出发,匀速向点B运动,连接 , 设的长为 , 的长为 , 则关于的函数图形如图2所示,其中函数图象最低点 , 则的周长为 .
17. 如图1,中,点P从A点出发,匀速向点B运动,连接 , 设的长为 , 的长为 , 则关于的函数图形如图2所示,其中函数图象最低点 , 则的周长为 .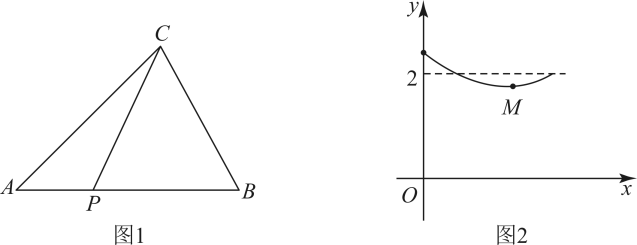 18. 新定义:为一次函数的“双减点”.若是某正比例函数的“双减点”,则关于y的不等式组的解集为 .
18. 新定义:为一次函数的“双减点”.若是某正比例函数的“双减点”,则关于y的不等式组的解集为 .三、解答题
-
19. 计算:(1)、;(2)、 .20. 某校为丰富同学们的课余生活,全面提高科学素养,提升思维能力和科技能力,开展了“最强大脑”邀请赛,现从七、八年级中各随机抽取了20名学生的初赛成绩(初赛成绩均为整数,满分为10分,9分及以上为优秀)统计、整理如下:
七年级抽取的学生的初赛成绩:6,6,7,7,7,8,8,8,8,8,9,9,9,9,9,9,9,10,10,10.
七、八年级抽取的学生的初赛成绩统计表:
年级
平均数
中位数
众数
方差
优秀率
七年级
8.5
a
八年级
8
7

根据以上信息,解答下列问题:
(1)、填空: , ;(2)、若该校八年级有900名学生参加初赛,规定满分才可进入复赛,估计八年级进入复赛的学生人数为多少人.(3)、根据以上数据,你认为七、八年级学生在“最强大脑”邀请赛中,哪个年级的学生初赛成绩更好?请说明理由;(写出一条理由即可)21. 如图,中, , 平分 , 交于点 , , . (1)、则点到直线的距离为 .(2)、求线段的长.22. 如图1,为线段上一动点,分别过点B、D作 , , 连接、 . 已知 , , , 设 .
(1)、则点到直线的距离为 .(2)、求线段的长.22. 如图1,为线段上一动点,分别过点B、D作 , , 连接、 . 已知 , , , 设 . (1)、用含的代数式表示的长为;(2)、求的最小值;(3)、根据(2)中的规律和结论,请模仿图1在网格中(图2)构图并求代数式的最小值.23. 为提升青少年的身体素质,某市在全市中小学推行“阳光体育”活动,某中学为满足学生的需求,准备再购买一些篮球和足球.如果分别用800元购买篮球和足球,则购买篮球的个数比足球的个数少2个,已知足球的单价为篮球单价的 .(1)、求篮球、足球的单价分别为多少元?(2)、学校计划购买篮球、足球共60个,如果购买足球m()个,总费用为w元,请写出w与m的函数关系式;(3)、在(2)的条件下学校计划总费用不多于5200元,那么应如何安排购买方案才能使费用最少,最少费用应为多少?
(1)、用含的代数式表示的长为;(2)、求的最小值;(3)、根据(2)中的规律和结论,请模仿图1在网格中(图2)构图并求代数式的最小值.23. 为提升青少年的身体素质,某市在全市中小学推行“阳光体育”活动,某中学为满足学生的需求,准备再购买一些篮球和足球.如果分别用800元购买篮球和足球,则购买篮球的个数比足球的个数少2个,已知足球的单价为篮球单价的 .(1)、求篮球、足球的单价分别为多少元?(2)、学校计划购买篮球、足球共60个,如果购买足球m()个,总费用为w元,请写出w与m的函数关系式;(3)、在(2)的条件下学校计划总费用不多于5200元,那么应如何安排购买方案才能使费用最少,最少费用应为多少?