吉林省长春市净月高新区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $202 3^{0}$ 的结果是（）

A、2023 B、1 C、0 D、 $\frac{1}{2023}$

查看试题解析
2. 芯片是指内含集成电路的硅片，在我们日常生活中的手机、电脑、电视、家用电器等领域都会使用到，它是高端制造业的核心基石．目前我国的芯片制造工艺已经达到了 $14 n m$ （纳米），已知 $1 n m = 1 \times 1 0^{- 9} m$ ，将 $14 n m$ 用科学记数法可表示（）m．（）

A、 $14 \times 1 0^{- 9}$ B、 $1.4 \times 1 0^{- 9}$ C、 $1.4 \times 1 0^{- 10}$ D、 $1.4 \times 1 0^{- 8}$

查看试题解析
3. 若一个点的坐标为 $(- 2 ， - 1)$ ，则这个点在如图所示的平面直角坐标系上的位置可能是（）

A、点 $A$ B、点 $B$ C、点 $C$ D、点 $D$

查看试题解析
4. 下列分式中，最简分式是（）

A、 $\frac{x^{2} - y^{2}}{x + y}$ B、 $\frac{3 y}{- 15 x}$ C、 $\frac{x + 1}{x^{2} + 1}$ D、 $\frac{x + 1}{x^{2} + 2 x + 1}$

查看试题解析
5. 某班甲、乙、丙、丁四位同学最近4次英语听说模拟测试成绩（单位：分，满分30分）的平均数和方差如表所示：

甲
乙
丙
丁
平均数
$29.54$
$29.55$
$29.55$
$29.54$
方差
$6.7$
$6.6$
$6.9$
$6.9$
根据表中数据，成绩好且发挥稳定的同学是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 如图，点 $A$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，过点 $A$ 作 $x$ 轴的垂线，垂足为点 $B$ ，点 $C$ 在 $y$ 轴上，若 $△ A B C$ 的面积为 $2$ ，则 $k$ 的值为（）

A、 $- 2$ B、 $2$ C、 $- 4$ D、 $4$

查看试题解析
7. 如图，小红作了如下操作：分别以A，C为圆心，大于 $\frac{1}{2} A C$ 长为半径作弧，两弧分别相交于点B，D，依次连接A，B，C，D，则下列说法一定正确的是（）

A、 $A B = A C$ B、 $A C = B D$ C、 $A C ⊥ B D$ D、四边形 $A B C D$ 是正方形

查看试题解析
8. 近视眼镜是一种为了矫正视力，让人们可以清晰看到远距离物体的凹透镜片．研究发现，近视眼镜的度数y（度）与镜片焦距x（m）的函数关系如图所示，则下列说法中错误的是（）

A、镜片焦距x的值越大，近视眼镜的度数y的值越小 B、图中曲线是反比例函数的图象（其中一支） C、当焦距x为 $0.3 m$ 时，近视眼镜的度数y约为300度 D、对于每一个镜片焦距x，都有唯一的近视度数y与它对应

查看试题解析

二、填空题

9. 要使分式 $\frac{1}{x - 5}$ 有意义，则x需满足的条件是．

查看试题解析
10. 化简： $\frac{2}{1 - x} - \frac{2 x}{1 - x}$ 的结果为．

查看试题解析
11. 如图，平行四边形 $A B C D$ 中， $∠ A B C$ 的平分线 $B E$ 交 $A D$ 于 $E$ ， $A B = 3$ ， $B C = 5$ ，则 $D E$ 的长为．

查看试题解析
12. 小明参加“强国有我”主题演讲比赛，其演讲形象、内容、效果三项的成绩分别是 $70$ 分、 $90$ 分、 $80$ 分．若将三项得分依次按 $2 ： 4 ： 4$ 的比例确定最终成绩，则小明的最终比赛成绩为分．

查看试题解析
13. 如图，直线 $y_{1} = x + 3$ 分别与x轴、y轴交于点A和点C，直线 $y_{2} = - x + 3$ 分别与x轴、y轴交于点B和点C，点 $P (m ， 2)$ 是 $△ A B C$ 内部（包括边上）的一点，则m的最大值与最小值之差为．

查看试题解析
14. 如图，矩形 $A B C D$ 的对角线相交于点O，过点O作 $O G ⊥ A C$ ，交 $A B$ 于点G，连接 $C G$ ，若 $∠ B O G = 15 °$ ，则 $∠ B C G$ 的度数是．

查看试题解析

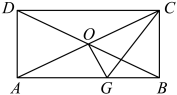
三、解答题

15. 先化简 $\frac{x + 2}{x + 1} \div \frac{x^{2} - 4}{2 x + 2}$ ，再从 $- 2$ ， $- 1$ ， $1$ ， $2$ 中选一个合适的数作为 $x$ 的值代入求值．

查看试题解析
16. 某毕业班班主任打算购买笔记本和书签作为毕业礼物送给学生 $.$ 已知书签的单价比笔记本的单价便宜 $1$ 元．且用 $440$ 元购买的书签的数量与用 $480$ 元购买的笔记本的数量一样．求笔记本和书签的单价．

查看试题解析
17. 图①、图②均为7×6的正方形网格，点A、B、C在格点(小正方形的顶点)上．

(1)、在图①中确定格点D，并画出一个以A、B、C、D为顶点的四边形，使其为轴对称图形；

(2)、在图②中确定格点E，并画出一个以A、B、C、E为顶点的四边形，使其为中心对称图形．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 是边 $B C$ 的中点，过点 $A$ ， $D$ 分别作 $B C$ 与 $A B$ 的平行线，相交于点 $E$ ，连接 $E C$ ， $A D$ ， $D E$ 与 $A C$ 交于点 $O$ ．

(1)、求证：四边形 $A D C E$ 是矩形；

(2)、当 $∠ B A C = 90 °$ 时，求证：四边形 $A D C E$ 是正方形．

查看试题解析
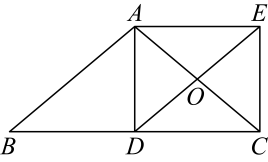19. 为了解八年级学生的体质健康状况 $.$ 某校在八年级学生中随机抽取了 $45$ 名学生进行体质检测（满分 $10$ 分，最低 $5$ 分），并按照男生、女生把成绩整理如下：

平均数
中位数
众数
方差
男生
$7.36$
$7.5$
$c$
$2.07$
女生
$a$
$b$
$7$
$1.96$
根据上述信息，解答下列问题：

(1)、求抽取的女生人数；

(2)、根据统计图可知 $a =$ ， $b =$ ， $c =$ ．

查看试题解析
20. 如图，一次函数 $y_{1} = k x + b$ 的图象与反比例函数 $y_{2} = \frac{m}{x}$ 的图象相交于 $A (- 2 ， n) 、 B (3 ， - 1)$ 两点，与 $y$ 轴相交于点 $C$ ．

(1)、求一次函数与反比例函数的解析式；

(2)、若点 $D$ 与点 $C$ 关于 $x$ 轴对称，求 $△ A B D$ 的面积．

查看试题解析

21. 为了燃气使用安全，燃气公司要求所有工业用户必须安装燃气报警器，当空气中燃气浓度达到一定量时，报警系统就会报警并切断燃气阀门以保证安全，在检测人员用标准天然气气瓶去检测燃气报警器有效性时，检测人员每分钟记录一次空气中燃气浓度．如表中记录了连续

5

分钟内

6

个时间点的燃气浓度．

时间 $(m i n)$	$0$	$1$	$2$	$3$	$4$	$5$
燃气浓度 $(%)$	$0$	$3$	$6$	$9$	$12$	$15$

【探索发现】

(1)、

①

建立如图所示平面直角坐标系，横轴表示检测时间

x (m i n)

，纵轴表示空气中的燃气浓度

y (%)

，图中已经描出以表格中数据为坐标的部分点，请你将表格中剩余的点描出；

$②$ 观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，求出这条直线所对应的函数表达式，如果不在同一条直线上，请说明理由．

(2)、预测第分钟时，系统会发出警报；

(3)、报警后，若无人发现，再过分钟系统会自动切断．

查看试题解析

22. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ，对角线 $B D$ 的垂直平分线与边 $A D ， B C$ 分别相交于点M、N．

(1)、求证：四边形 $B N D M$ 是菱形；

(2)、若 $B D = 24$ ，菱形 $B N D M$ 的面积为120，求菱形 $B N D M$ 的周长．

查看试题解析
23. $[$ 问题呈现 $]$ 如图是李老师在一节课中的例题内容．
例 $1$ ：已知：如图，在 $▱$ $A B C D$ 中， $E$ 、 $F$ 是对角线 $A C$ 上的两点，并且 $A E = C F$ ．求证： $B E = D F$ ．
证明： $∵$ 四边形 $A B C D$ 是平行四边形，
$∴ . A B = C D$ （平行四边形的对边相等）， $A B ∥ C D$ （平行四边形的定义）．
$∴ ∠ B A E = ∠ D C F$ ．
又 $∵ A E = C F$ ，
$∴ △ A B E$ ≌ $△ C D F$ ．
$∴ B E = D F$ ．

(1)、【结论应用】
如图 $①$ ，在平行四边形 $A B C D$ 中， $E . F$ 是对角线 $A C$ 上的两点，且 $A E = C F$ ，连接 $B F$ 、 $D E$ ，请判断四边形 $B F D E$ 的形状，并证明；

(2)、【拓展提升】
如图 $②$ ，点 $G . H$ 是正方形 $A B C D$ 对角线 $A C$ 上的两点且 $A G = C H$ ， $G H = A B$ ； $E$ 、 $F$ 分别是 $A B$ 、 $C D$ 的中点；
①则四边形 $E H F G$ 的形状为；
②若正方形 $A B C D$ 的面积为 $16$ ．则四边形 $E H F G$ 的面积为．

查看试题解析
24. 如图，在平面直角坐标系中，点 $A$ 的坐标为 $(6 ， 4)$ ，过点A分别作 $A B ⊥ x$ 轴于点 $B$ ， $A C ⊥ y$ 轴于点 $C$ ，一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $P (2 ， 4)$ ．

(1)、当直线 $y = k x + b$ 经过点 $B$ 时，求 $k$ 的值；

(2)、当直线 $y = k x + b$ 与 $B C$ 平行时，则 $b$ 的值为；

(3)、若直线 $y = k x + b$ 将矩形 $O B A C$ 的面积平分，求此时一次函数的解析式；

(4)、作点 $C$ 关于直线 $y = k x + b$ 的对称点 $C^{'}$ ，当点 $B$ 、 $P$ 、 $C^{'}$ 三点共线时，请直接写出此时 $C^{'}$ 的坐标．

查看试题解析

	甲	乙	丙	丁
平均数	$29.54$	$29.55$	$29.55$	$29.54$
方差	$6.7$	$6.6$	$6.9$	$6.9$

	平均数	中位数	众数	方差
男生	$7.36$	$7.5$	$c$	$2.07$
女生	$a$	$b$	$7$	$1.96$