天津市北辰区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 二次根式有意义,则x的取值范围是( )A、 B、 C、 D、2. 计算的结果为( )A、2 B、 C、4 D、3. 某书店对上季度该店中国古代四大名著的销售量统计如表,依统计数据,为更好地满足读者需求,该书店决定本季度购进中国古代四大名著时多购进一些《西游记》,你认为最影响该书店决策的统计量是( )
书名
《西游记》
《水浒传》
《三国演义》
《红楼梦》
销量
180
120
125
85
A、平均数 B、众数 C、中位数 D、方差4. 在中,如果三边满足关系 , 则的直角是( )A、 B、 C、 D、不能确定5. 甲、乙两人在相同条件下,各射击10次,经计算:甲射击成绩的平均数是9环,方差是1.4;乙射击成绩的平均数是9环,方差是0.8,下列说法中一定正确的是( )A、甲的总环数大于乙的总环数 B、甲的成绩比乙的成绩稳定 C、甲、乙成绩的众数相同 D、乙的成绩比甲的成绩波动小6. 四边形ABCD是平行四边形,下列说法错误的是( ) A、当时,四边形ABCD是矩形 B、当时,四边形ABCD是菱形 C、当时,四边形ABCD是矩形 D、当平分时,四边形ABCD是菱形7. 已知一次函数的函数值随的增大而减小,则该函数的图象大致是( )A、
A、当时,四边形ABCD是矩形 B、当时,四边形ABCD是菱形 C、当时,四边形ABCD是矩形 D、当平分时,四边形ABCD是菱形7. 已知一次函数的函数值随的增大而减小,则该函数的图象大致是( )A、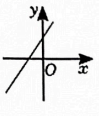 B、
B、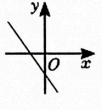 C、
C、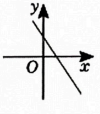 D、
D、 8. 如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0, 2),(-1,-1)(2, -1),则顶点D的坐标是( )
8. 如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0, 2),(-1,-1)(2, -1),则顶点D的坐标是( ) A、(-3, 2) B、(3, -2) C、(3, 2) D、(2, 2)9. 已知方程的解为 , 则一次函数的图象与轴交点的坐标为( )A、 B、 C、 D、10. 已知点 , 在一次函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、不能确定11. 已知一次函数 , 下列说法不正确的是( )A、图象与x轴的交点坐标是 B、图象经过第一、二、四象限 C、y随x的增大而减小 D、图象与两坐标轴围成的三角形面积为212. 如图1,点从矩形的顶点出发,沿以的速度匀速运动到点 , 图2是点运动时,的面积随时间变化的关系图像,则的值为( )
A、(-3, 2) B、(3, -2) C、(3, 2) D、(2, 2)9. 已知方程的解为 , 则一次函数的图象与轴交点的坐标为( )A、 B、 C、 D、10. 已知点 , 在一次函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、不能确定11. 已知一次函数 , 下列说法不正确的是( )A、图象与x轴的交点坐标是 B、图象经过第一、二、四象限 C、y随x的增大而减小 D、图象与两坐标轴围成的三角形面积为212. 如图1,点从矩形的顶点出发,沿以的速度匀速运动到点 , 图2是点运动时,的面积随时间变化的关系图像,则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 比较大小:24.14. 将直线沿y轴向下平移2个单位,平移后的直线与y轴的交点坐标是 .15. 若三角形的两边长为6和8,要使其成为直角三角形,则第三边的长为 .16. 如图,在矩形纸片中, , , 将其折叠,使点与点重合,折痕为 . 的长为 .
 17. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
17. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:甲:函数的图象经过点 , ;
乙;随的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述写出满足上述性质的一个函数表达式为 .
18. 如图,正方形和正方形中,点N在上, , , D是的中点,那么的长是 .
三、解答题
-
19. 计算(1)、;(2)、20. 如图,菱形中,对角线 , 交于点O, , . 求证:四边形是矩形.
 21. 某学校为了解学生某一周参加家务劳动的情况,从各年级共1500名学生中随机抽取了部分学生,对其参加家务劳动的次数进行了统计,会制出如下的统计图①和图②.根据相关信息,解答下列问题:
21. 某学校为了解学生某一周参加家务劳动的情况,从各年级共1500名学生中随机抽取了部分学生,对其参加家务劳动的次数进行了统计,会制出如下的统计图①和图②.根据相关信息,解答下列问题: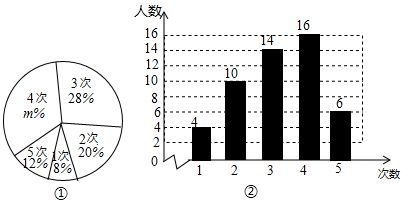 (1)、本次接受随机抽样调查的学生人数为 , 图①中m的值为;(2)、求统计的这组参加家务劳动次数数据的众数、中位数和平均数;(3)、根据统计的这组参加家务劳动次数数据,估计该校学生中这周参加家务劳动次数大于3的学生人数.22. 已知一次函数的图象与正比例函数的图像交于点 .
(1)、本次接受随机抽样调查的学生人数为 , 图①中m的值为;(2)、求统计的这组参加家务劳动次数数据的众数、中位数和平均数;(3)、根据统计的这组参加家务劳动次数数据,估计该校学生中这周参加家务劳动次数大于3的学生人数.22. 已知一次函数的图象与正比例函数的图像交于点 . (1)、求 , 的解析式;(2)、直接在图中画出两个函数图象;(3)、当时, . (填“>”,“=”或“<”)23. 某年级430名师生秋游,计划租用8辆客车,现有甲、乙两种型号客车,它们的载客量和租金如下表:
(1)、求 , 的解析式;(2)、直接在图中画出两个函数图象;(3)、当时, . (填“>”,“=”或“<”)23. 某年级430名师生秋游,计划租用8辆客车,现有甲、乙两种型号客车,它们的载客量和租金如下表:甲种客车
乙种客车
载客量(座/辆)
60
45
租金(元/辆)
550
450
(1)、设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;(2)、当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?