天津市滨海新区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 若是二次根式,则x的取值范围是( )A、 B、 C、 D、2. 下列等式正确的是( )A、 B、 C、 D、3. 如果一个三角形的三边长分别为1,1, , 那么这个三角形是( )A、锐角三角形 B、等边三角形 C、钝角三角形 D、等腰直角三角形4. 下列函数中,y是x的正比例函数的是( )A、 B、 C、 D、5. 下表记录了甲、乙、丙、丁四名射箭选手10次测试成绩的平均数与方差:
甲
乙
丙
丁
平均数(分)
9.2
9.5
9.5
9.2
方差
3.6
3.6
7.4
8.1
要选择一名成绩好且发挥稳定的选手参加射箭比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁6. 若平行四边形两个内角的度数比为 , 则其中较小的内角是( )A、45° B、60° C、90° D、120°7. 一次函数的图像不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如果点与点都在直线上,那么m,n的大小关系是( )A、 B、 C、 D、无法判断9. 如图,点O是矩形的对角线的中点,E是边的中点, , , 则线段的长为( ) A、5 B、6 C、8 D、1010. 若点是x轴上的一个动点,它与x轴上表示3的点的距离是y,则y关于x的函数解析式为( )A、 B、 C、 D、11. 如图,P正方形对角线上一点. , E,F分别为垂足,若 , 则的长为( )
A、5 B、6 C、8 D、1010. 若点是x轴上的一个动点,它与x轴上表示3的点的距离是y,则y关于x的函数解析式为( )A、 B、 C、 D、11. 如图,P正方形对角线上一点. , E,F分别为垂足,若 , 则的长为( ) A、5 B、4 C、3 D、12. 如图,平面直角坐标系 中,点 的坐标为 , 轴,垂足为 ,点 从原点 出发向 轴正方向运动,同时,点 从点 出发向点 运动,当点 到达点 时,点 、 同时停止运动,若点 与点 的速度之比为 ,则下列说法正确的是( )
A、5 B、4 C、3 D、12. 如图,平面直角坐标系 中,点 的坐标为 , 轴,垂足为 ,点 从原点 出发向 轴正方向运动,同时,点 从点 出发向点 运动,当点 到达点 时,点 、 同时停止运动,若点 与点 的速度之比为 ,则下列说法正确的是( )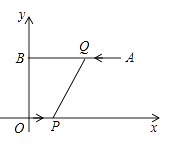 A、线段 始终经过点 B、线段 始终经过点 C、线段 始终经过点 D、线段 不可能始终经过某一定点
A、线段 始终经过点 B、线段 始终经过点 C、线段 始终经过点 D、线段 不可能始终经过某一定点二、填空题
-
13. 计算: = .14. 将直线 向上平移2个单位长度,平移后直线的解析式为 .
15. 某学校拟招聘一名数学教师,一位应聘者在说课和答辩两个环节的成绩分别是85分和90分,学校认为说课环节更重要,对说课和答辩分别赋予6和4的权.则该应聘者的平均成绩是分.16. 已知 , , 那么代数式的值 .17. 平面直角坐标系中,直线与相交于点 , 有下列结论: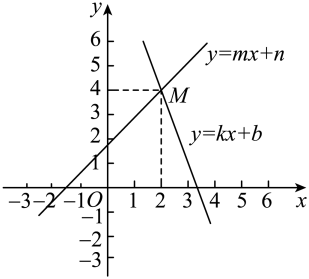
①关于x,y的方程组的解是;
②关于x的不等式的解集是;
③关于x的方程的解是;
④ .
其中,正确的是(填写序号).
三、解答题
-
18. 在如图所示的6×6网格中,每个小正方形的边长均为1,点A,B,C均落在格点上.
 (1)、的长等于;(2)、请在如图所示的网格中,用无刻度的直尺,
(1)、的长等于;(2)、请在如图所示的网格中,用无刻度的直尺,①画出线段、使平分线段 , 其中D为格点;
②画出线段 , 使 , 其中E是格点.
(简要说明画法,不要求证明)
19. 计算:(1)、;(2)、 .20. 某校为了解初中学生每天在校体育活动的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的初中学生人数为 ▲ , 图①中m的值为 ▲ ;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
21. 如图,在中, , . 求中边上的高是多少? 22. 下面是小明设计的作正方形ABCD的尺规作图过程.
22. 下面是小明设计的作正方形ABCD的尺规作图过程.已知:中, . .
求作:正方形 .
作法:如图,

⒈以点A为图心.长为半径作弧;
⒉以点C为圆心,长为半径作弧;
⒊两弧交于点D,点B和点D在异侧;
⒋连接 , , 所以四边形是正方形.
(1)、根据小明设计的尺规作图过程,使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∵ ▲ , ▲ ,
∴四边形是平行四边形.( )(填推理的依据)
∵ ,
∴四边形是矩形.( )(填推理的依据)
又∵ ,
∴四边形是正方形.( )(填推理的依据)
23. 已知:如图,四边形是矩形,分别延长 , 到点E,F,使 , , 连接 . (1)、求证:四边形是菱形;(2)、连接 , 如果四边形的周长是 , , 求的长.24. 在“看图说故事”活动中,某学习小组结合图像设计了一个问题情境.
(1)、求证:四边形是菱形;(2)、连接 , 如果四边形的周长是 , , 求的长.24. 在“看图说故事”活动中,某学习小组结合图像设计了一个问题情境.
已知小明家、食堂、图书馆依次在同一条直线上.食堂离小明家 . 图书馆离小明家 . 周末,小明从家出发,匀速走了到食堂;在食堂停留吃早餐后,匀速走了到图书馆;在图书馆读报停留 , 然后匀速走了返回家.给出的图像反映了这个过程中小明离家的距离与离开家的时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:小明离开家的时间/min
8
20
40
小明离家的距离/km
(2)、填空:①食堂到图书馆的距离为km;
②小明从图书馆返回家中的速度为;
③当小明离家的距离为时,他离开家的时间为min.
(3)、当时,请直接写出y关于x的函数解析式.25. 如图,在平面直角坐标系中,为坐标原点,矩形的顶点 , , 将矩形的一个角沿直线折叠,使得点落在对角线上的点处,折痕与轴交于点 . (1)、线段的长度;(2)、求直线所对应的函数表达式;(3)、若点在线段上,在线段上是否存在点 , 使以 , , P,为顶点的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、线段的长度;(2)、求直线所对应的函数表达式;(3)、若点在线段上,在线段上是否存在点 , 使以 , , P,为顶点的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.