山东省济南市历城区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、3. 已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、菱形的对角线相等 B、矩形的对角线相等且互相平分 C、平行四边形是轴对称图形 D、对角线互相垂直且相等的四边形是正方形5. 如图,在平行四边形中,的平分线交于点E,的平分线交于点F,若 , , 则的长是( )
2. 下列各式从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、3. 已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、菱形的对角线相等 B、矩形的对角线相等且互相平分 C、平行四边形是轴对称图形 D、对角线互相垂直且相等的四边形是正方形5. 如图,在平行四边形中,的平分线交于点E,的平分线交于点F,若 , , 则的长是( )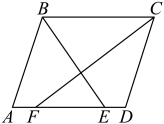 A、3.5 B、3 C、2 D、16. 如图,将绕点顺时针方向旋转得到 , 若 , 连接 , 则等于( )
A、3.5 B、3 C、2 D、16. 如图,将绕点顺时针方向旋转得到 , 若 , 连接 , 则等于( )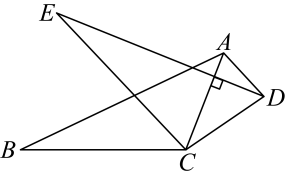 A、 B、 C、 D、7. 如图,直线经过点 , 则关于x的不等式的解集是( )
A、 B、 C、 D、7. 如图,直线经过点 , 则关于x的不等式的解集是( )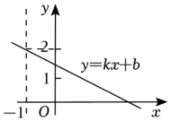 A、 B、 C、 D、8. 关于x的分式方程 +5= 有增根,则m的值为( )A、1 B、3 C、4 D、59. 如图,RtABC中, , , D、E分别为AB,AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE=( )
A、 B、 C、 D、8. 关于x的分式方程 +5= 有增根,则m的值为( )A、1 B、3 C、4 D、59. 如图,RtABC中, , , D、E分别为AB,AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE=( )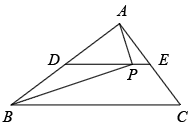 A、1 B、 C、 D、210. 如图,菱形沿射线平移,得到菱形 , 延长 , 相交于点M,延长 , 相交于点N,若 , , 则的长是( )
A、1 B、 C、 D、210. 如图,菱形沿射线平移,得到菱形 , 延长 , 相交于点M,延长 , 相交于点N,若 , , 则的长是( )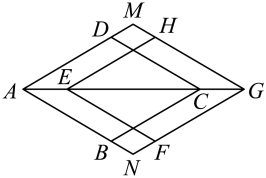 A、3 B、4 C、 D、
A、3 B、4 C、 D、二、填空题
-
11. 分解因式:a2-4a+4=12. 如图,正方形与正五边形的边重合,连接 , 则的度数是 .
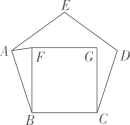 13. 如图,两个全等的矩形纸片重叠在一起,矩形的长和宽分别是8和4,则重叠部分的四边形的周长等于 .
13. 如图,两个全等的矩形纸片重叠在一起,矩形的长和宽分别是8和4,则重叠部分的四边形的周长等于 .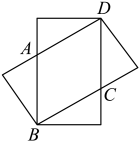 14. 如图,将一块正方形空地划出部分区域阴影部分进行绿化,绿化后一边减少了 , 另一边减少了 , 剩余面积为的矩形空地,则原正方形空地的边长为 .
14. 如图,将一块正方形空地划出部分区域阴影部分进行绿化,绿化后一边减少了 , 另一边减少了 , 剩余面积为的矩形空地,则原正方形空地的边长为 .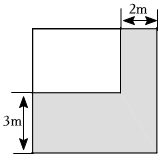 15. 关于x的方程有两个实数根,则k的取值范围是 .16. 如图,已知中, , , 两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接 , 则线段的最小值是 .
15. 关于x的方程有两个实数根,则k的取值范围是 .16. 如图,已知中, , , 两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接 , 则线段的最小值是 .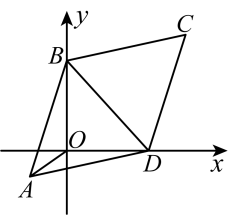
三、解答题
-
17. 解不等式组,并写出它的整数解.18. 先化简,再求值: , 再从 , , , 四个数中选一个合适的数作为a的值代入求值.19. 解分式方程:(1)、(2)、20. 解一元二次方程:(1)、(2)、21. 如图,在中,E,F为对角线所在直线上的两个点,且 , 连接 , . 求证: .
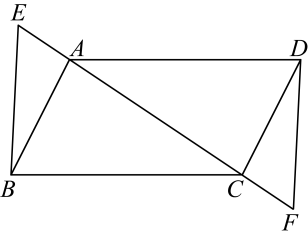 22. 如图,在平面直角坐标系中,的三个顶点分别是 , , .
22. 如图,在平面直角坐标系中,的三个顶点分别是 , , . (1)、将以点为旋转中心旋转180°,画出旋转后对应的;(请用黑色水笔描黑)(2)、平移 , 若A的对应点的坐标为 , 则平移距离为 ▲ , 画出平移后对应的;(请用黑色水笔描黑)(3)、若将绕某一点旋转可以得到 , 请直接写出旋转中心的坐标为 ▲ .23. 已知:正方形中,点E,M分别在边 , 上.
(1)、将以点为旋转中心旋转180°,画出旋转后对应的;(请用黑色水笔描黑)(2)、平移 , 若A的对应点的坐标为 , 则平移距离为 ▲ , 画出平移后对应的;(请用黑色水笔描黑)(3)、若将绕某一点旋转可以得到 , 请直接写出旋转中心的坐标为 ▲ .23. 已知:正方形中,点E,M分别在边 , 上. (1)、如图1, , 垂足为点G,求证:;(2)、如图2,点F,N分别在边 , 上,若 , 请判断和的大小关系,并说明理由.24. 为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,甲水果的进价比乙水果的进价低20%,水果店用1000元购进甲种水果比用1200元购进乙种水果的重量多10千克,已知甲,乙两种水果的售价分别为6元/千克和8元/千克.(1)、求甲、乙两种水果的进价分别是多少?(2)、若水果店购进这两种水果共150千克,其中甲种水果的重量不低于乙种水果重量的2倍,则水果店应如何进货才能获得最大利润,最大利润是多少?25. 已知中, , 于点M,点D在直线上, , 垂足为点E, , 垂足为点F.
(1)、如图1, , 垂足为点G,求证:;(2)、如图2,点F,N分别在边 , 上,若 , 请判断和的大小关系,并说明理由.24. 为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,甲水果的进价比乙水果的进价低20%,水果店用1000元购进甲种水果比用1200元购进乙种水果的重量多10千克,已知甲,乙两种水果的售价分别为6元/千克和8元/千克.(1)、求甲、乙两种水果的进价分别是多少?(2)、若水果店购进这两种水果共150千克,其中甲种水果的重量不低于乙种水果重量的2倍,则水果店应如何进货才能获得最大利润,最大利润是多少?25. 已知中, , 于点M,点D在直线上, , 垂足为点E, , 垂足为点F.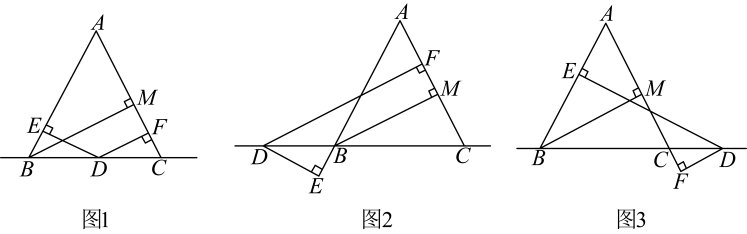 (1)、如图1,点D在边上时,小明同学利用①三角形全等知识和②图形等面积法两种方法发现了 , , 三线段之间的数量关系,请直接写出三线段之间的数量关系是;(2)、如图2,图3,当点D在点B左边或者在点C右边的直线上时,问题(1)中 , , 三线段的数量关系是否还成立?若成立请选择一个图形进行证明,若不成立,请在图2或图3中选择一个图形,写出三线段新的数量关系,并进行证明.26. 在中, , , 点D,E是边 , 的中点,连接 , , 点M,N分别是和的中点,连接 .
(1)、如图1,点D在边上时,小明同学利用①三角形全等知识和②图形等面积法两种方法发现了 , , 三线段之间的数量关系,请直接写出三线段之间的数量关系是;(2)、如图2,图3,当点D在点B左边或者在点C右边的直线上时,问题(1)中 , , 三线段的数量关系是否还成立?若成立请选择一个图形进行证明,若不成立,请在图2或图3中选择一个图形,写出三线段新的数量关系,并进行证明.26. 在中, , , 点D,E是边 , 的中点,连接 , , 点M,N分别是和的中点,连接 .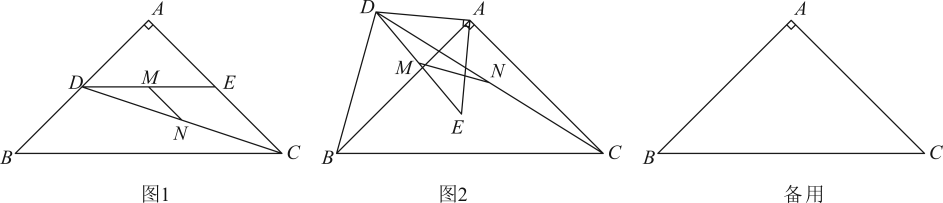 (1)、如图1,与的数量关系是;(2)、如图2,将绕点A顺时针旋转,连接 , 请写出和的数量关系,并就图2的情形说明理由;(3)、在的旋转过程中,当B,D,E三点共线时,求线段的长.
(1)、如图1,与的数量关系是;(2)、如图2,将绕点A顺时针旋转,连接 , 请写出和的数量关系,并就图2的情形说明理由;(3)、在的旋转过程中,当B,D,E三点共线时,求线段的长.