新疆维吾尔自治区昌吉回族自治州昌吉市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列各式中是最简二次根式的是( )A、 B、 C、 D、2. 下列各组数据中的三个数,可作为三边长构成直角三角形的是( )A、4,5,6 B、2,3,4 C、11,12,13 D、8,15,173. 下列计算正确的是( )A、 B、 C、 D、4. 如图,在▱ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
 A、1.5cm B、2cm C、2.5cm D、3cm5. 如果函数y=(2﹣k)x+5是关于x的一次函数,且y随x的值增大而减小,那么k的取值范围是( )A、k≠0 B、k<2 C、k>2 D、k≠26. 某人开车从家出发去植物园游玩,设汽车行驶的路程为S(千米),所用时间为t(分),S与t之间的函数关系如图所示.若他早上8点从家出发,汽车在途中停车加油一次,则下列描述中,不正确的是( )
A、1.5cm B、2cm C、2.5cm D、3cm5. 如果函数y=(2﹣k)x+5是关于x的一次函数,且y随x的值增大而减小,那么k的取值范围是( )A、k≠0 B、k<2 C、k>2 D、k≠26. 某人开车从家出发去植物园游玩,设汽车行驶的路程为S(千米),所用时间为t(分),S与t之间的函数关系如图所示.若他早上8点从家出发,汽车在途中停车加油一次,则下列描述中,不正确的是( ) A、汽车行驶到一半路程时,停车加油用时10分钟 B、汽车一共行驶了60千米的路程,上午9点5分到达植物园 C、加油后汽车行驶的速度为60千米/时 D、加油后汽车行驶的速度比加油前汽车行驶的速度快7. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数均是9.2环,方差分别为 , , , ,则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁8. 如图,直线与直线交于点 , 则不等式的解集是( )
A、汽车行驶到一半路程时,停车加油用时10分钟 B、汽车一共行驶了60千米的路程,上午9点5分到达植物园 C、加油后汽车行驶的速度为60千米/时 D、加油后汽车行驶的速度比加油前汽车行驶的速度快7. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数均是9.2环,方差分别为 , , , ,则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁8. 如图,直线与直线交于点 , 则不等式的解集是( ) A、 B、 C、 D、9. 如图1,点从矩形的顶点出发,沿以的速度匀速运动到点 , 图2是点运动时,的面积随时间变化的关系图象,则的值为( )
A、 B、 C、 D、9. 如图1,点从矩形的顶点出发,沿以的速度匀速运动到点 , 图2是点运动时,的面积随时间变化的关系图象,则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 若二次根式 有意义,则x的取值范围是 .11. 将一次函数的图象向下平移2个单位,所得图象对应的函数表达式为 .12. 如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为.
 13. 如图,已知菱形 的对角线 交于点 为 的中点,若 ,则菱形的周长为.
13. 如图,已知菱形 的对角线 交于点 为 的中点,若 ,则菱形的周长为.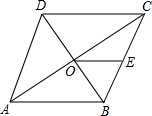 14. 已知一次函数(k为常数,且),y随x的增大而减小,当时,函数有最大值5,则k的值是 .15. 如图,直线与轴、轴分别交于点和点 , 点是线段上的一点,若将沿折叠,点恰好落在轴上的处,若是轴负半轴上一动点,且是以为腰的等腰三角形,则的坐标为 .
14. 已知一次函数(k为常数,且),y随x的增大而减小,当时,函数有最大值5,则k的值是 .15. 如图,直线与轴、轴分别交于点和点 , 点是线段上的一点,若将沿折叠,点恰好落在轴上的处,若是轴负半轴上一动点,且是以为腰的等腰三角形,则的坐标为 .
三、解答题
-
16. 计算:(1)、(2)、17. 如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD BC.
 (1)、求证:四边形ABCD是平行四边形;(2)、若AC⊥BD,AC=8,BD=6,求平行四边形ABCD的面积.18. 勾股定理是重要的数学定理之一,是用代数思想解决几何问题的最重要的工具,也是数形结合的纽带.
(1)、求证:四边形ABCD是平行四边形;(2)、若AC⊥BD,AC=8,BD=6,求平行四边形ABCD的面积.18. 勾股定理是重要的数学定理之一,是用代数思想解决几何问题的最重要的工具,也是数形结合的纽带. (1)、应用场景——在数轴上画出表示无理数的点.
(1)、应用场景——在数轴上画出表示无理数的点.如图1,在数轴上找出表示3的点A,过点A作直线L垂直于 , 在L上取点B,使 , 以原点O为圆心,为半径作弧,求弧与数轴的交点C表示的数.
(2)、应用场景2——解决实际问题.如图2,秋千静止时,踏板离地的垂直高度m,将它往前推6m至C处时,水平距离m,踏板离地的垂直高度m,它的绳索始终拉直,求绳索的长.
19. 某校为了增强学生的疫情防控意识.组织全校2000名学生进行了疫情防控知识竞赛.从中随机抽取了n名学生的竞赛成绩(满分100分),分成四组:A: ;B: ;C: ;D: ,并绘制出如下不完整的统计图: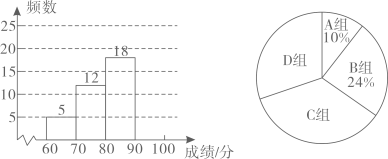 (1)、填空:n=;(2)、补全频数分布直方图;(3)、抽取的这n名学生成绩的中位数落在组;(4)、若规定学生成绩 为优秀.估算全校成绩达到优秀的人数.20. 学校开展大课间活动,某班需要购买A,B两种跳绳.已知购买2根A型跳绳和1根B型跳绳共需元;购买3根A型跳绳和2根B型跳绳共需元.(1)、购买1根A型跳绳和1根B型跳绳各需多少元?(2)、若班级计划购买A,B两型跳绳共根,B型跳绳个数不少于A型跳绳个数的2倍,设购买A型跳绳m根,求购买跳绳所需最少费用是多少元?
(1)、填空:n=;(2)、补全频数分布直方图;(3)、抽取的这n名学生成绩的中位数落在组;(4)、若规定学生成绩 为优秀.估算全校成绩达到优秀的人数.20. 学校开展大课间活动,某班需要购买A,B两种跳绳.已知购买2根A型跳绳和1根B型跳绳共需元;购买3根A型跳绳和2根B型跳绳共需元.(1)、购买1根A型跳绳和1根B型跳绳各需多少元?(2)、若班级计划购买A,B两型跳绳共根,B型跳绳个数不少于A型跳绳个数的2倍,设购买A型跳绳m根,求购买跳绳所需最少费用是多少元?

