云南省大理州祥云县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 飞沫一般认为是直径大于5微米(5微米=0.000005米)的含水颗粒.飞沫传播是新型冠状病毒的主要传播途径之一,日常面对面说话、咳嗽、打喷嚏都可能造成飞沫传播.因此有效的预防措施是戴口罩并尽量与他人保持1米以上社交距离.将0.000005用科学记数法表示应为( ).A、 B、 C、 D、4. 甲、乙两人参加射击比赛,每人10次射击的平均成绩恰好都是9.2环,方差分别是 , 在本次射击测试中成绩最稳定的是( )A、甲 B、乙 C、甲、乙一样 D、无法确定5. 下列各组数中,不能构成直角三角形的是( )A、 B、 C、 D、6. 关于函数 ,下列结论正确的是( )A、图象必经过点 B、图象经过第一、二、三象限 C、当 时, D、y随x的增大而增大7. 下列运算中正确的是( )A、 B、 C、 D、8. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( )
2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 飞沫一般认为是直径大于5微米(5微米=0.000005米)的含水颗粒.飞沫传播是新型冠状病毒的主要传播途径之一,日常面对面说话、咳嗽、打喷嚏都可能造成飞沫传播.因此有效的预防措施是戴口罩并尽量与他人保持1米以上社交距离.将0.000005用科学记数法表示应为( ).A、 B、 C、 D、4. 甲、乙两人参加射击比赛,每人10次射击的平均成绩恰好都是9.2环,方差分别是 , 在本次射击测试中成绩最稳定的是( )A、甲 B、乙 C、甲、乙一样 D、无法确定5. 下列各组数中,不能构成直角三角形的是( )A、 B、 C、 D、6. 关于函数 ,下列结论正确的是( )A、图象必经过点 B、图象经过第一、二、三象限 C、当 时, D、y随x的增大而增大7. 下列运算中正确的是( )A、 B、 C、 D、8. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( ) A、 B、 C、 D、9. 已知点和点都在直线上,若 , 则和的大小关系是( )A、 B、 C、 D、不能确定10. 如图所示,在四边形中, , 要使四边形成为平行四边形还需要条件( )
A、 B、 C、 D、9. 已知点和点都在直线上,若 , 则和的大小关系是( )A、 B、 C、 D、不能确定10. 如图所示,在四边形中, , 要使四边形成为平行四边形还需要条件( ) A、 B、 C、 D、11. 如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
A、 B、 C、 D、11. 如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )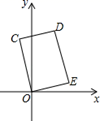 A、3 B、 C、 D、412. 如图,在 中, , , 是 的中垂线, 是 的中垂线,已知 的长为 ,则阴影部分的面积为( )
A、3 B、 C、 D、412. 如图,在 中, , , 是 的中垂线, 是 的中垂线,已知 的长为 ,则阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若二次根式在实数范围内有意义,则的取值范围是 .14. 分解因式: .15. 如图,点是的角平分线上的一点,过点作交于点 , , 若 , , 则 .
 16. 如图,函数的图像经过点 , 则关于的不等式的解集为 .
16. 如图,函数的图像经过点 , 则关于的不等式的解集为 .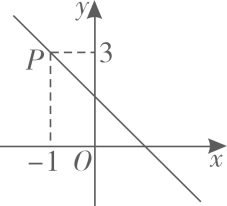
三、解答题
-
17. 计算 .18. 先化简,再求值: ,其中x=2+19. 某公司计划购买A、B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运材料,且A型机器人搬运材料所用的时间与B型机器人搬运材料所用的时间相同.求A、B两种型号的机器人每小时分别搬运多少材料?20. 某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,因此学校随机抽取了部分同学就兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
 (1)、设学校这次调查共抽取了n名学生,直接写出n的值;(2)、请你补全条形统计图;(3)、设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?21. 如图,已知直线与x轴、轴分别交于A,B两点,且 , x轴上一点C的坐标为 , P是直线上一点.
(1)、设学校这次调查共抽取了n名学生,直接写出n的值;(2)、请你补全条形统计图;(3)、设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?21. 如图,已知直线与x轴、轴分别交于A,B两点,且 , x轴上一点C的坐标为 , P是直线上一点. (1)、求直线的函数表达式;(2)、连接和 , 当点P的横坐标为2时,求的面积.22. 如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)、求直线的函数表达式;(2)、连接和 , 当点P的横坐标为2时,求的面积.22. 如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.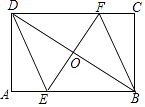 (1)、求证:四边形BEDF是平行四边形;(2)、当四边形BEDF是菱形时,求EF的长.23. 学校购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需要26元;3只A型节能灯和2只B型节能灯共需要29元;(1)、求1只A型和1只B型节能灯的售价各是多少元?(2)、学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯的数量的3倍,不少于B型节能灯数量的2倍,有几种购买方案,哪种方案最省钱?24. 如图,已知直线y=kx+b与直线y=-x-9平行,且y=kx+b还过点(2,3),与y轴交于A点.
(1)、求证:四边形BEDF是平行四边形;(2)、当四边形BEDF是菱形时,求EF的长.23. 学校购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需要26元;3只A型节能灯和2只B型节能灯共需要29元;(1)、求1只A型和1只B型节能灯的售价各是多少元?(2)、学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯的数量的3倍,不少于B型节能灯数量的2倍,有几种购买方案,哪种方案最省钱?24. 如图,已知直线y=kx+b与直线y=-x-9平行,且y=kx+b还过点(2,3),与y轴交于A点. (1)、求A点坐标;(2)、若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;(3)、在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.
(1)、求A点坐标;(2)、若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;(3)、在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.