云南省昆明市呈贡区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式中，是最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{5}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{8}$

查看试题解析
2. 矩形不一定具有的特征是（）

A、对角线垂直 B、对角线相等 C、四个角都是直角 D、对角线互相平分

查看试题解析
3. 根据某市统计局发布的该市近5年的年度GDP增长率的有关数据，经济学家评论说，该市近5年的年度GDP增长率相当平稳，从统计学的角度看，“增长率相当平稳”说明这组数据的（）比较小．

A、中位数 B、平均数 C、众数 D、方差

查看试题解析
4. 下列计算中，结果错误的是（）

A、 $\sqrt{45} - \sqrt{5} = 2 \sqrt{5}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{27} \div \sqrt{3} = 3$ D、 $3 \sqrt{2} \times \sqrt{2} = 6$

查看试题解析
5. 一次函数y=-4x+8图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 若 $\sqrt{5 - x}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x < 5$ B、 $x \leq 5$ C、 $x > 5$ D、 $x ≥ 5$

查看试题解析
7. 在 $△ A B C$ 中，若 $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别是a，b，c，则下列条件中，不能判定 $△ A B C$ 是直角三角形的是（）

A、 $(a + b) (a - b) = c^{2}$ B、 $∠ C - ∠ B = ∠ A$ C、 $a = \sqrt{5}$ ， $b = \sqrt{12}$ ， $c = \sqrt{13}$ D、 $a ： b ： c = 3 ： 4 ： 5$

查看试题解析
8. 如图，在 $▱ A B C D$ 中， $A B = 5$ ， $A D = 8$ ， $∠ A B C$ 的平分线 $B E$ 交 $A D$ 于点E，则DE的长是（）

A、4 B、3 C、3.5 D、2

查看试题解析
9. 如图，一次函数 $y = k x + b$ 与 $y = - x + 5$ 的图象的交点坐标为 $(2 ， 3)$ ，则关于x的方程 $- x + 5 = k x + b$ 的解为（）

A、 ${\begin{array}{l} x = 3 \\ x = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ x = 3 \end{array}$ C、 $x = 3$ D、 $x = 2$

查看试题解析
10. 把直线 $y = 6 x$ 向上平移后得到直线 $A B$ ，若直线 $A B$ 经过点 $(m ， n)$ ，且 $n - 6 m = 4$ ，则直线 $A B$ 的表达式为（）

A、 $y = - 6 x + 4$ B、 $y = - 6 x - 4$ C、 $y = 6 x - 4$ D、 $y = 6 x + 4$

查看试题解析
11. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证．那么对于这个图中各部分的面积关系，说法不一定成立的是（）

A、 $S_{矩形 N F G D} = S_{矩形 E F M B}$ B、 $S_{△ A B C} = S_{△ A D C}$ C、 $S_{△ A N F} = S_{矩形 F M C G}$ D、 $S_{△ A E F} = S_{△ A N F}$

查看试题解析
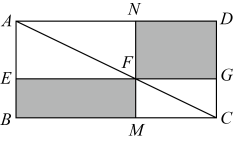12. 如果正整数a、b、c满足等式 $a^{2} + b^{2} = c^{2}$ ，那么正整数a、b、c叫做勾股数．某同学将自探究勾股数的过程列成下表，观察表中每列数的规律，可知 $x + y$ 的值为（）
a
b
c
3
4
5
8
6
10
15
8
17
24
10
26
…
…
…
x
14
y

A、67 B、34 C、98 D、73

查看试题解析

二、填空题

13. $\sqrt{{(- 5)}^{2}}$ = ．

查看试题解析
14. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = \sqrt{10}$ ， $2 A B^{2} + A C^{2} + B C^{2} =$ ．

查看试题解析
15. 如图，正方形 $A B C D$ 的顶点B、C都在直角坐标系的x轴上，点D的坐标是 $(2 ， 3)$ ，则直线 $B D$ 的解析式为．

查看试题解析
16. 如图，将菱形纸片 $A B C D$ 折叠，使点A恰好落在菱形对角线的交点O处，折痕为 $E F$ ，则点E、F分别为边 $A B$ 、 $A D$ 的中点．若 $O E = 2$ ， $∠ A = 120 °$ ，则 $E F =$ ．

查看试题解析

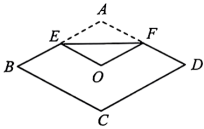
三、解答题

17. 计算： $(\sqrt{3} + 1) \times (\sqrt{3} - 1) + \sqrt{48} + {(π - 1)}^{0} + {(- \frac{1}{3})}^{- 1}$ ．

查看试题解析
18.

(1)、我们知道像3，4，5这样三个整数是一组勾股数，那么 $3 k$ ， $4 k$ ， $5 k$ （k是正整数）是一组勾股数吗？如果是，请证明；如果不是，请说明理由；

(2)、如果a，b，c是一组勾股数，那么 $a k$ ， $b k$ ， $c k$ （k是正整数）也是一组勾股数吗？如果是，请证明；如果不是，请说明理由．

查看试题解析
19. 已知直线 $y = k x + b$ 经过点 $A (8 ， 0)$ ， $B (4 ， 4)$ ．

(1)、求直线 $A B$ 的解析式；

(2)、若直线 $y = x - 2$ 与直线 $A B$ 相交于点C，求点C的坐标；

(3)、根据图象，写出关于x的不等式 $x > k x + b + 2$ 的解集．

查看试题解析
20. 为了加强对青少年防溺水安全教育，4月初某校开展了“远离溺水，珍爱生命”的防溺水安全知识比赛．下面是从参赛学生中随机收集到的20名学生的成绩（单位：分）：
87 99 86 89 91 91 95 96 87 97

91 97 96 86 96 89 100 91 99 97

整理数据：

成绩（分）

86

87

89

91

95

96

97

99

100

学生人数（人）

2

2

2

4

1

3

3

2

1

分析数据：

平均数

众数

中位数

93

a

b

解决问题：

(1)、直接写出：上面表格中的 $a =$ ， $b =$ ；

(2)、若成绩达到95分及以上为“优秀”等级，求“优秀”等级所占的百分率为；

(3)、请估计该校1500名学生中成绩达到95分及以上的学生人数．

查看试题解析
21. 学校计划为“用英语讲中国故事”演讲比赛购买奖品，已知购买4个A奖品和3个B奖品共需165元；购买6个A奖品和2个B奖品共需210元．

(1)、求A，B两种奖品的单价；

(2)、学校准备购买A，B两种奖品共20个，且A奖品的数量不少于B奖品数量的 $\frac{2}{5}$ ，请设计出最省钱的购买方案，并说明理由．

查看试题解析
22. 如图，在四边形 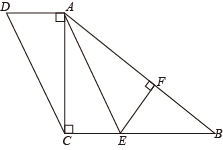$A B C D$ 中， $∠ A C B = ∠ C A D = 90 °$ ，点 $E$ 在 $B C$ 边上， $A E ∥ D C$ ， $E F ⊥ A B$ ，垂足为 $F$ ．

(1)、求证：四边形 $A E C D$ 是平行四边形；

(2)、若 $A E$ 平分 $∠ B A C$ ， $B E = 5$ ， $\frac{B F}{B E} = \frac{4}{5}$ ，求 $B F$ 和 $A D$ 的长．

查看试题解析
23. 阅读材料：像 $(\sqrt{3} + 1) (\sqrt{3} - 1) = 2$ ， $\sqrt{a} \times \sqrt{a} = a (a \geq 0)$ …这种两个含二次根式的代数式相乘，积不含二次根式，我们称这两个代数式互为有理化因式．在进行二次根式运算时，利用有理化因式可以化去分母中的根号．
例如： $\frac{1}{2 \sqrt{2}} = \frac{\sqrt{2}}{2 \sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{4}$ ； $\frac{\sqrt{3} + 1}{\sqrt{3} - 1} = \frac{(\sqrt{3} + 1)}{(\sqrt{3} - 1) (\sqrt{3} + 1)} = 2 + \sqrt{3}$ ．
解答下列问题：

(1)、 $\sqrt{6}$ 的有理化因式是， $\sqrt{3} + 2$ 的有理化因式是．

(2)、观察下面的变形规律，请你猜想： $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ．
$\frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$ ， $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}} = \sqrt{4} - \sqrt{3}$ …

(3)、利用上面的方法，请化简：
$\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + ⋯ ⋯ + \frac{1}{\sqrt{2022} + \sqrt{2023}}$ ．

查看试题解析
24. 在四边形ABCD中，AD∥BC，AB=8cm，AD=16cm，BC=22cm，∠ABC=90°．点P从点A出发，以1cm/s的速度向点D运动，点Q从点C同时出发，以3cm/s的速度向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t秒．

(1)、当t=时，四边形ABQP成为矩形？

(2)、当t=时，以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形？

(3)、四边形PBQD是否能成为菱形？若能，求出t的值；若不能，请说明理由，并探究如何改变Q点的速度（匀速运动），使四边形PBQD在某一时刻为菱形，求点Q的速度．

查看试题解析

成绩（分）	86	87	89	91	95	96	97	99	100
学生人数（人）	2	2	2	4	1	3	3	2	1

a	b	c
3	4	5
8	6	10
15	8	17
24	10	26
…	…	…
x	14	y

平均数	众数	中位数
93	a	b