云南省部分地州县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 若在实数范围内有意义,则实数x的取值范围是( )A、 B、 C、 D、2. 以下列各组数为三角形的三边长,其中能构成直角三角形的是( )A、2,3,4 B、6,8,9 C、1,2, D、5,12,133. 下列点中,在函数的图象上的是( )A、 B、 C、 D、4. 下列运算中,正确的是( )A、 B、 C、 D、5. 一次函数的图象如图所示,当时,x的取值范围是( )
 A、 B、 C、 D、6. 如图,在中, , , , 点分别是的中点,则四边形的周长为( )
A、 B、 C、 D、6. 如图,在中, , , , 点分别是的中点,则四边形的周长为( ) A、 B、 C、 D、7. 在平面直角坐标系中,若将直线向上平移a个单位长度得到直线 , 则a的值为( )A、0 B、2 C、3 D、48. 若直角三角形的两边长分别为a、b,且满足 , 则该直角三角形的第三边长为( )A、5 B、5或 C、4 D、或49. 一段时间内,一家童装店为了解某种童装的销售情况,对各种尺码童装的销量进行了统计分析.童装店老板最关心的统计量是( )A、平均数 B、中位数 C、众数 D、方差10. 如图,四边形是平行四边形,对角线、相交于点O,在条件:①;②;③;④平分中,选择一个条件,使得四边形是菱形,可选择的条件是( )
A、 B、 C、 D、7. 在平面直角坐标系中,若将直线向上平移a个单位长度得到直线 , 则a的值为( )A、0 B、2 C、3 D、48. 若直角三角形的两边长分别为a、b,且满足 , 则该直角三角形的第三边长为( )A、5 B、5或 C、4 D、或49. 一段时间内,一家童装店为了解某种童装的销售情况,对各种尺码童装的销量进行了统计分析.童装店老板最关心的统计量是( )A、平均数 B、中位数 C、众数 D、方差10. 如图,四边形是平行四边形,对角线、相交于点O,在条件:①;②;③;④平分中,选择一个条件,使得四边形是菱形,可选择的条件是( ) A、①②③ B、①②④ C、①③④ D、②③④11. 甲、乙两车沿着公路从A地开往B地,汽车离开A地的距离y(km)与行驶时间t(h)的对应关系如图所示,则下列结论错误的是( )
A、①②③ B、①②④ C、①③④ D、②③④11. 甲、乙两车沿着公路从A地开往B地,汽车离开A地的距离y(km)与行驶时间t(h)的对应关系如图所示,则下列结论错误的是( ) A、甲、乙两车行驶3小时后相遇 B、甲车的平均速度为 C、乙车的平均速度为 D、乙车比甲车先到达B地12. 如图,正方形的对角线交于点O,E是正方形外一点,且 , 若 , , 则的长为( )
A、甲、乙两车行驶3小时后相遇 B、甲车的平均速度为 C、乙车的平均速度为 D、乙车比甲车先到达B地12. 如图,正方形的对角线交于点O,E是正方形外一点,且 , 若 , , 则的长为( ) A、 B、9 C、 D、
A、 B、9 C、 D、二、填空题
-
13. 已知正比例函数的y值随x的增大而增大,请写出一个符合条件的函数表达式 .14. 在甲、乙两位射击运动员的10次考核成绩中,两人的考核成绩的平均数相同,方差分别为 , , 则考核成绩更为稳定的运动员是 .15. 如图,菱形ABCD的面积是24,对角线AC=6,则菱形ABCD周长是 .
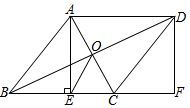
 16. 如图, , , , 一个小球从点A处出发,沿着方向匀速滚向点O,机器人同时从点B出发,沿直线匀速去拦截小球,恰好在C处截住了小球,如果小球与机器人的速度相同,那么机器人行走的路程的长为 .
16. 如图, , , , 一个小球从点A处出发,沿着方向匀速滚向点O,机器人同时从点B出发,沿直线匀速去拦截小球,恰好在C处截住了小球,如果小球与机器人的速度相同,那么机器人行走的路程的长为 .
三、解答题
-
17. 计算: .18. 如图,货船和轮船从码头A同时出发,其中,货船沿着北偏西方向以5海里/小时的速度匀速航行,轮船沿着北偏东方向以12海里/小时的速度航行,1小时后,两船分别到达B,C点.求B,C两点之间的距离.
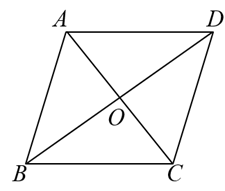
 19. 如图,在平行四边形中,E、F分别是、上的点,且 . 求证: .
19. 如图,在平行四边形中,E、F分别是、上的点,且 . 求证: . 20. 共享单车是高校学生最喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可以随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了部分出行学生使用共享单车的情况,并整理成如下表:
20. 共享单车是高校学生最喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可以随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了部分出行学生使用共享单车的情况,并整理成如下表:使用次数
0
1
2
3
4
5
人数
5
7
12
14
9
3
根据以上表格信息,解答下列问题:
(1)、这组数据的中位数是;众数是;(2)、这部分出行学生平均每人使用共享单车约多少次?(结果保留整数)(3)、若该校某天有1500名学生出行,请你估计这天使用共享单车次数在4次及4次以上的学生有多少人?21. 如图,在中, , 平分 , 交于点D, , . (1)、求点D到直线的距离;(2)、求线段的长.22. 学校为奖励在全县联合考试中成绩优秀的同学,计划购买甲、乙两种奖品.已知购买甲种奖品6件和乙种奖品5件需花费390元,购买甲种奖品3件和乙种奖品7件需花费330元.(1)、求甲、乙两种奖品的单价;(2)、学校计划购买甲、乙两种奖品共180件,其中购买乙种奖品的件数不超过甲种奖品件数的2倍,学校分别购买甲、乙两种奖品多少件才能使总费用最少?
(1)、求点D到直线的距离;(2)、求线段的长.22. 学校为奖励在全县联合考试中成绩优秀的同学,计划购买甲、乙两种奖品.已知购买甲种奖品6件和乙种奖品5件需花费390元,购买甲种奖品3件和乙种奖品7件需花费330元.(1)、求甲、乙两种奖品的单价;(2)、学校计划购买甲、乙两种奖品共180件,其中购买乙种奖品的件数不超过甲种奖品件数的2倍,学校分别购买甲、乙两种奖品多少件才能使总费用最少?