云南省昭通市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 一个三角形的两边长分别为 , , 则这个三角形的第三条边的长可能是( )A、 B、 C、 D、2. 下列各式中计算正确的是( )A、 B、 C、 D、3. 下列实数的取值能使代数式有意义的是( )A、 B、 C、 D、4. 在中, , 则的长度为( )A、6 B、8 C、10 D、125. 下列各曲线表示的与的关系中,是的函数的是( )A、
 B、
B、 C、
C、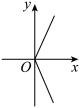 D、
D、 6. 如图,八角帽又称“红军帽”,其帽顶近似正八边形.那么正八边形的一个外角的大小为( )
6. 如图,八角帽又称“红军帽”,其帽顶近似正八边形.那么正八边形的一个外角的大小为( ) A、 B、 C、 D、7. 如图,在中,分别以 , 为圆心,大于的长为半径画弧,两弧交于点 , , 作直线 , 分别交 , 于点 , , 连接 . 若 , 则的度数为( )
A、 B、 C、 D、7. 如图,在中,分别以 , 为圆心,大于的长为半径画弧,两弧交于点 , , 作直线 , 分别交 , 于点 , , 连接 . 若 , 则的度数为( ) A、 B、 C、 D、8. 现有一组统计数据: , , , , , , . 对于不同的 , 下列统计量不会发生改变的是( )A、众数、中位数 B、平均数、方差 C、平均数、中位数 D、众数、方差9. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、四个角都相等的四边形是正方形 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、有一组邻边相等且有一个角是直角的平行四边形是正方形10. 如图,在中,平分 , , , 若 , , 则的长为( )
A、 B、 C、 D、8. 现有一组统计数据: , , , , , , . 对于不同的 , 下列统计量不会发生改变的是( )A、众数、中位数 B、平均数、方差 C、平均数、中位数 D、众数、方差9. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、四个角都相等的四边形是正方形 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、有一组邻边相等且有一个角是直角的平行四边形是正方形10. 如图,在中,平分 , , , 若 , , 则的长为( ) A、6 B、7 C、8 D、911. 一列单项式按以下规律排列: , , , , , , , , 则第个单项式是( )A、 B、 C、 D、12. 在同一平面直角坐标系中,函数和的图象大致为( ).A、
A、6 B、7 C、8 D、911. 一列单项式按以下规律排列: , , , , , , , , 则第个单项式是( )A、 B、 C、 D、12. 在同一平面直角坐标系中,函数和的图象大致为( ).A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 的值是 .14. 分解因式: .15. 若 , 则的值是 .16. 在中, , , , 点是边上的点,且 , 则的面积为 .
三、解答题
-
17. 计算:18. 如图, , 求证: .
 19. 某工厂共有工人1200人,厂长为了解车间工人的工作效率,某一天随机抽查了20名工人当天生产零件的个数情况,统计如下:
19. 某工厂共有工人1200人,厂长为了解车间工人的工作效率,某一天随机抽查了20名工人当天生产零件的个数情况,统计如下:生产零件的个数
52
53
54
55
56
57
人数
1
2
7
6
3
1
(1)、这20名工人这一天生产零件个数的众数为 , 中位数为 .(2)、若把一天生产零件个数不低于56个的员工称为“A级工人”,请估计该工厂“A级工人”的人数.20. 为了测量一条两岸平行的河流的宽度,三个数学活动小组设计了不同的方案,他们在河南岸的点B处测得河北岸的树AB恰好在B的正北方向,测量方案如下表:课题
测量河流宽度
工具
测量角度的仪器,标杆,皮尺等
小组
第一小组
第二小组
第三小组
测量方案
观测者从B点向东走到点,此时测得点恰好在东南方向上.
观测者从B点出发,沿着南偏西的方向走到点 , 此时恰好测得 .
观测者从B点向东走到点,在点插上一面标杆,继续向东走相同的路程到达点后,一直向南走到点 , 使得树、标杆、人在同一直线上.
测量示意图


 (1)、第一小组认为要知道河宽 , 只需要知道线段的长度.(2)、第二小组测得米,则 .(3)、第三小组认为只要测得就能得到河宽 , 你认为第三小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.21. 在网格中建立如图所示的平面直角坐标系,其中、、、 .
(1)、第一小组认为要知道河宽 , 只需要知道线段的长度.(2)、第二小组测得米,则 .(3)、第三小组认为只要测得就能得到河宽 , 你认为第三小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.21. 在网格中建立如图所示的平面直角坐标系,其中、、、 .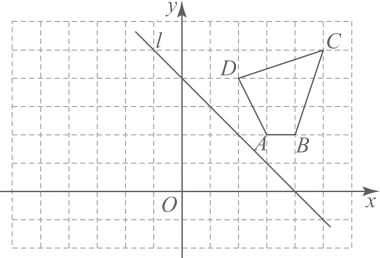 (1)、请作出四边形关于轴对称的四边形 , 并写出点的对应点的坐标;(2)、在直线上找一点 , 使得的周长最小,在图中标出的位置,并写出点的坐标(保留画图过程的痕迹).22. 某班计划采购、两种类型的跳绳,已知购买型跳绳的单价是型跳绳的倍;用300元购买型跳绳的数量比购买型跳绳的数量多2根.(1)、求A、两种类型跳绳的单价.(2)、该班准备采购、两种类型的跳绳共30根,且型跳绳的数量不超过型跳绳数量的倍,请给出最省钱的购买方案,并求出最少费用.
(1)、请作出四边形关于轴对称的四边形 , 并写出点的对应点的坐标;(2)、在直线上找一点 , 使得的周长最小,在图中标出的位置,并写出点的坐标(保留画图过程的痕迹).22. 某班计划采购、两种类型的跳绳,已知购买型跳绳的单价是型跳绳的倍;用300元购买型跳绳的数量比购买型跳绳的数量多2根.(1)、求A、两种类型跳绳的单价.(2)、该班准备采购、两种类型的跳绳共30根,且型跳绳的数量不超过型跳绳数量的倍,请给出最省钱的购买方案,并求出最少费用.

