云南省德宏州2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{7}$ C、 $\sqrt{8}$ D、 $\sqrt{0.5}$

查看试题解析
2. 以下列各组数据为三角形的三边，能构成直角三角形的是（）

A、4cm，8cm，7cm B、2cm，2cm，2cm C、2cm，2cm，4cm D、6cm，8cm ，10cm

查看试题解析
3. 如图所示的函数图象对应的函数解析式可能是（）

A、 $y = 3 x$ B、 $y = 3 x + 2$ C、 $y = \frac{2}{x}$ D、 $y = - x + 3$

查看试题解析
4. 下列各式中，计算正确的是（）

A、 $\sqrt{(- 2)^{2}} = - 2$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$

查看试题解析
5. 如图，在 $▱ A B C D$ 中，对角线 $A C 、 B D$ 相交于点O，点E是 $B C$ 的中点，若 $C D = 8$ ，则 $O E$ 的长为（）

A、4 B、3 C、5 D、6

查看试题解析
6. 关于函数 $y = - x + 5$ ，下列结论中正确的是（）

A、函数图象经过点 $(1 ， 6)$ B、函数图象经过第一、二、四象限 C、函数图象与 $x$ 轴的交点为 $(0 ， 5)$ D、不论 $x$ 取何值，总有 $y > 0$

查看试题解析
7. 若实数 $a$ ， $b$ 满足 $\sqrt{a - 2} + | b + 3 | = 0$ ，则 $b^{a}$ 的值是（）

A、 $- 3$ B、3 C、 $- 9$ D、9

查看试题解析
8. 下列说法中正确的是（）

A、一组数据2，2，3，4的中位数是2 B、一组数据的2，4，1，4，2众数是4 C、甲、乙两人进行射击测试，每人10次射击成绩的平均数均是9.1环，方差分别为：
$S_{甲}^{2} = 0.51$ ， $S_{乙}^{2} = 0.64$ ，则甲的射击成绩较稳定
D、小明的三次数学检测成绩85分，90分，97分，这三次成绩的平均数是92分

查看试题解析
9.
如图，▱ABCD的对角线AC、BD相交于点O，且AC+BD=16，CD=6，则△ABO的周长是（　　）

A、10 B、14 C、20 D、22

查看试题解析
10. 如图，已知 $R t △ O A B$ 的两条直角边 $O A = 2$ ， $A B = 3$ ，以O为圆心， $O B$ 的长为半径画弧，交数轴的正半轴于点P，则点P所表示的数介于（）

A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间

查看试题解析
11. 如图所示的函数图象反映的过程是：小徐从家去菜地浇水，又去玉米地除草，然后回家，其中x表示时间，y表示小徐离他家的距离．读图可知菜地离小徐家的距离为（）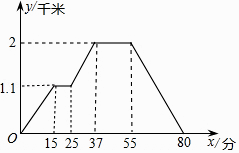

A、1.1千米 B、2千米 C、15千米 D、37千米

查看试题解析
12. 如图，正方形 $A B C D$ 的边长为12，将正方形折叠，使顶点 $D$ 落在 $B C$ 边上的点 $E$ 处，折痕为 $G H$ . 若 $B E ： E C = 2 ： 1$ ，则线段 $D H$ 的长是（）

A、 $\frac{20}{3}$ B、8 C、 $\frac{16}{3}$ D、6

查看试题解析

二、填空题

13. 若代数式 $\sqrt{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
14. 若一次函数 $y = k x - 2$ 的函数值 $y$ 随着自变量x值的增大而减小，则 $k =$ （写出一个满足条件的值）．

查看试题解析
15. 已知菱形 $A B C D$ 的周长为16，其中 $∠ A B C = 60 °$ ，则菱形 $A B C D$ 的面积为．（结果保留根号）

查看试题解析
16. 弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形．如果大正方形的面积是 $13$ ，小正方形的面积是 $1$ ，直角三角形的较短直角边长为 $a$ ，较长直角边长为 $b$ ，那么 ${(a + b)}^{2}$ 的值是．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{27} + \sqrt{12} - \sqrt{8}$

(2)、 $(2 \sqrt{32} - 2 \sqrt{\frac{1}{2}}) \div \sqrt{2}$

查看试题解析
18. 如图，四边形 $A B C D$ 是平行四边形，对角线AC，BD相交于点O， $∠ D B C = ∠ A C B$ ．求证：四边形 $A B C D$ 是矩形．

查看试题解析
19. 某班欲从甲、乙两名同学中推出一名同学，参加学校组织的数学素质测试竞赛，首先在班内对甲、乙两名同学进行了数与代数、图形与几何、统计与概率、综合与实践的测试，他们的各项成绩（百分制）如下表所示：
学生
数与代数
图形与几何
统计与概率
综合与实践
甲
85
89
92
94
乙
94
92
85
80

(1)、如果各项成绩同等重要，计算甲、乙两名同学的平均成绩，从他们的成绩看，应该推选谁？

(2)、若数与代数、图形与几何、统计与概率、综合与实践的成绩按 $4 ： 3 ： 2 ： 1$ 的比确定，计算甲、乙两名同学的平均成绩，从他们的成绩看，应该推选谁？

查看试题解析
20. 自动感应水龙头使用方便，没有开启关闭的操作，相对于传统水龙头节水率达到60%以上，为了节约用水，某校安装了一批自动感应水龙头.该批自动感应水龙头的示意图如下：在距离洗手台面 $25 c m$ 的点C处连接着出水口D所在水管，水管AB的点E处安装有红外线感应装置，已知出水口D到点C的距离为 $12 c m$ ，出水口D到点E的距离为 $15 c m$ ，且 $C D ⊥ A B$ ，求红外线感应装置到洗手台面的高度 $B E$ 的长为多少？

查看试题解析
21. 根据《环境空气质量指数（ $A Q I$ ）技术规定（试行）》规定：空气污染指数划分为六档，对应于空气质量的六个级别，指数越大，级别越高，说明污染越严重，对人体健康的影响也越明显.当空气污染指数达到0～50时为一级；51～100时为二级，101～150时为三级；151～200时为四级；201～300时为五级，空气污染指数大于300，空气质量级别为六级，其中一级属于优，二级属于良，三级属于轻度污染，四级属于中度污染，五级属于重度污染，六级为严重污染．某校数学兴趣小组随机抽取了2023年1—6月份所在城市某些天的空气质量检测数据，并绘制成如下图、表：
级别
指数
天数
频率
一级
0～50
8
0.16
二级
51～100
20
0.4
三级
101～150
$a$
0.3
四级
151～200
5
$b$
五级
201～300
1
0.02
六级
大于300
1
0.02
请根据以上图、表提供的信息，解答下列问题：

(1)、统计表中的 $a =$ ▲ ， $b =$ ▲ ；并补全条形统计图；

(2)、根据以上数据的分析，请你估计2023年该城市全年的空气污染指数属于轻度污染和中度污染的大概共有多少天？（一年按365天计算）

查看试题解析
22. 为保证学生每天一小时体育运动，某班计划购买一批体育用品，用于开展“阳光体育动起来”为主题的课外运动．经调查，了解到甲、乙两个体育用品店的优惠活动如下，甲店：所有体育用品按原价8折出售；乙店：一次购买体育用品总额不超过 $200$ 元的按原价出售，超过 $200$ 元的部分打6折．

(1)、以 $x$ （单位：元）表示体育用品原价， $y$ （单位：元）表示购买总额，分别就两家体育用品店的优惠方式写出 $y$ 关于 $x$ 的函数解析式；

(2)、如何选择这两家体育用品店去购买体育用品更省钱？

查看试题解析
23. 如图，点 $A$ ， $F$ ， $C$ ， $D$ 在同一条直线上，点 $B$ ， $E$ 分别在直线 $A D$ 的两侧，且 $A B = D E$ ， $∠ A = ∠ D$ ， $A F = D C$ .

(1)、求证：四边形 $B F E C$ 是平行四边形

(2)、若四边形 $B F E C$ 是菱形， $∠ A B C = 90 °$ ， $A B = 4$ ， $B C = 3$ ，求 $A F$ 的长.

查看试题解析
24. 如图，已知直线 $y = \frac{3}{2} x + 3$ 分别交 $x$ 轴， $y$ 轴于A、C两点，直线 $B C$ 过点 $C$ 交 $x$ 轴于点 $B$ ，且 $O C ： O B = 1 ： 2$ ，点D是直线 $A C$ 上的一点且点D的横坐标为 $- 1$ .

(1)、求直线 $B C$ 的解析式；

(2)、已知点P是线段 $B C$ 上的一个动点，点 $Q$ 是 $x$ 轴上的一个动点，当 $△ D P Q$ 是等腰直角三角形时，求点P的坐标.

查看试题解析

学生	数与代数	图形与几何	统计与概率	综合与实践
甲	85	89	92	94
乙	94	92	85	80

级别	指数	天数	频率
一级	0～50	8	0.16
二级	51～100	20	0.4
三级	101～150	$a$	0.3
四级	151～200	5	$b$
五级	201～300	1	0.02
六级	大于300	1	0.02