云南省昆明市五华区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 使二次根式 $\sqrt{a - 3}$ 有意义的a的取值范围是（）

A、a>3 B、a<3 C、 $a \geq 3$ D、 $a \leq 3$

查看试题解析
2. 下列各组数中能作为直角三角形的三边长的是（）

A、1，2，3 B、1，1， $\sqrt{3}$ C、13，14，15 D、6，8，10

查看试题解析
3. 如图所示，数学活动课上，某兴趣小组要测量池塘两端 $A$ ， $B$ 的距离，他们先在平地上取一个点 $C$ ，从点 $C$ 不经过池塘可以直接到达点 $A$ 和点 $B$ ，连接 $A C$ ， $B C$ ，并分别找出 $A C$ ， $B C$ 的中点 $D$ ， $E$ ，连接 $D E$ ．并量出 $D E = 24 m$ ，则 $A$ ， $B$ 的距离为（）

A、 $48 m$ B、 $60 m$ C、 $80 m$ D、不能确定

查看试题解析
4. 《义务教育课程标准（2022年版）》首次把学生学会烹饪纳入劳动教育课程，并作出明确规定某班有七名同学已经学会烹饪的菜品种数依次为：3，5，4，6，3，3，4，则这组数据的众数、中位数和平均数分别是（）

A、3，4，4 B、4，3，4 C、3，3，4 D、4，4，3

查看试题解析
5. 下列关于函数 $y = \frac{1}{3} x$ 的结论正确的是（）

A、函数图象经过点 $(1 ， 3)$ B、函数图象经过第一、三象限 C、y随x的增大而减小 D、不论x为何值，总有 $y > 0$

查看试题解析
6. 下列各式中，运算正确的是（）

A、 $3 \sqrt{3} - \sqrt{3} = 3$ B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、 $2 + \sqrt{3} = 2 \sqrt{3}$ D、 $\sqrt{2} \times \sqrt{8} = 4$

查看试题解析
7. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）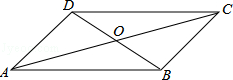

A、AB//DC，AD//BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB//DC，AD=BC

查看试题解析
8. 矩形具有而平行四边形不一定具有的性质是（）

A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分

查看试题解析
9. 下图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名同学的成绩，下列说法正确的是（）

A、甲同学平均分高，成绩波动较小 B、甲同学平均分高，成绩波动较大 C、乙同学平均分高，成绩波动较小 D、乙同学平均分高，成绩波动较大

查看试题解析
10. 王老师家，超市，公园自西向东依次在同一直线上，家到超市的距离，到公园的距离分别为200米，1000米．她从家出发匀速步行5分钟到达超市，停留3分钟后骑共享单车，以250米/分匀速行驶到公园．设王老师离超市的距离为s（单位：m），所用时间为t（单位：min），则下列表示s和t之间函数关系的图像中，正确的是（）

A、 B、 C、 D、

查看试题解析
11. 某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：
候选人
甲
乙
丙
丁
测试成绩（百分制）
面试
$86$
$92$
$90$
$83$
笔试
$90$
$83$
$83$
$92$
如果公司认为，作为公关人员面试成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．根据四人各自的平均成绩，公司将录取（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
12. 如图所示，已知直线 $y = n x + b$ 经过点 $A (- 2 ， - 4)$ 和点 $B (- 4 ， 0)$ ，直线 $y = m x$ 经过点 $A$ ，则关于 $x$ 的不等式 $n x + b \leq m x$ 的解集是（）

A、 $x ≤ - 2$ B、 $x > - 2$ C、 $x \geq - 2$ D、 $- 2 \leq x < 0$

查看试题解析

二、填空题

13. 计算： $\sqrt{18} \div \sqrt{2} =$ ．

查看试题解析
14. 如图，过正方形ABCD的顶点B作直线l，过点A、C作l的垂线，垂足分别为点E、F，若AE＝1，CF＝3，则AB的长度为．

查看试题解析
15. 如图所示，在 $△ A B C$ 中， $∠ C = 90 °$ ，点D为 $B C$ 边上一点，将 $△ A C D$ 沿 $A D$ 翻折得到 $△ A C^{'} D$ ，若点 $C^{'}$ 在 $A B$ 边上， $A C = 6 ， B C = 8$ ，则 $A D$ 的长为．

查看试题解析
16. 对于实数a，b，定义符号min{a，b}，其意义为：当a≥b时，min{a，b}=b；当a＜b时，min{a，b}=a.例如：min={2，﹣1}=﹣1，若关于x的函数y=min{2x﹣1，﹣x+3}，则该函数的最大值为.

查看试题解析

三、解答题

17. 计算： $(\sqrt{6} - 3) (\sqrt{6} + 3) + {(\sqrt{2} - 1)}^{2}$ ．

查看试题解析
18. 在正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长都是1，如图所示，点A，B，O都在格点上，求 $∠ A O B$ 的度数．

查看试题解析

19. 某校开展了安全知识宣传教育活动，为了解这次活动的效果，从该校七、八年级学生中各随机抽取20名学生进行测试，其中抽测的八年级学生成绩如下：

81 83 84 86 86 87 87 88 89 90

92 92 93 95 95 95 99 99 100 100

对七、八年级参加测试学生成绩整理如下：

	$80 \leq x < 85$	$85 \leq x < 90$	$90 \leq x < 95$	$95 \leq x \leq 100$
七年级	4	6	2	8
八年级	3	a	4	7

对两组数据分析如下：

	平均数	中位数	众数	方差
七年级	91	89	97	40.9
八年级	91	$b$	95	33.2

根据以上信息，解答下列问题：

(1)、填空：

a =

，

b =

；

(2)、样本数据中七年级甲同学和八年级乙同学的分数都是90分，把七、八年级各20名同学的分数按从高到底的顺序排列，同学的成绩在本年级更靠前（填“甲”或“乙”）；

(3)、如果把成绩在90分以上（含90分）定为优秀，那么该校八年级300名学生中，成绩为优秀的学生约有多少人？

查看试题解析

20. 如图，在平行四边形 $A B C D$ 中，E为线段 $A D$ 的中点，延长 $B E$ 与 $C D$ 的延长线交于点F，连接 $A F$ ， $B D$ ， $∠ B D F = 90 °$ ．

(1)、求证：四边形 $A B D F$ 是矩形；

(2)、若 $B C = 4$ ， $D F = 3$ ，求四边形 $A B C F$ 的面积S．

查看试题解析
21. 如图所示，一次函数 $y = - x + b$ 的图象分别与x，y轴交于A，B两点，点A的坐标为 $(6 ， 0)$ ，过点B的直线交x轴负半轴于点C，且 $O B ： O C = 3 ： 1$ ．

(1)、求点B的坐标；

(2)、求直线 $B C$ 的解析式；

(3)、若点 $P (m ， 2)$ 在 $△ A B C$ 的内部，直接写出m的取值范围．

查看试题解析
22. 勾股定理是初等几何中最重要的定理之一，它的证明方法很多，如图1是3世纪我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，通过对图形的切割、拼接，巧妙的利用面积关系证明了勾股定理．

(1)、定理证明：
图1是由四个全等的直角三角形围成的一个大正方形，中间的部分是一个小正方形（阴影）．如果直角三角形较小的直角边长为a，较大的直角边长为b，斜边长为c，请你根据图1证明勾股定理；

(2)、问题解决：
如图2，圆柱的底面半径为 $40 c m$ ，高为 $30 π c m$ ，蚂蚁在圆柱表面爬行，从点A爬到点B的最短路程是多少厘米？（结果保留π）

查看试题解析
23. 某书店制订了“读书节”活动计划，以下是活动计划的部分信息：
书本类别
A类
B类
进价（单位：元）
18
12
备注
用不超过16800元购进两类图书共1000本，A类图书不少于600本．

(1)、陈经理查看计划时发现：A类图书的标价是B类图书的1.5倍，若顾客用540元购买图书，单独购买A类图书的数量恰好比单独购买B类图书的数量少10本，请求出A，B两类图书的标价；

(2)、为了扩大影响，陈经理调整了销售方案：A类图书售价每本降低4元，B类图书价格不变．此时书店应如何进货才能获得最大利润？

查看试题解析
24. 在菱形 $A B C D$ 中， $∠ A B C = 60 °$ ，点 $P$ 是射线 $B D$ 上一动点，以 $A P$ 为边向右侧作等边 $Δ A P E$ ．

(1)、如图1，当点 $E$ 在菱形 $A B C D$ 内部或边上时，连接 $C E$ ．则 $B P$ 与 $C E$ 的数量关系是， $C E$ 与 $A D$ 的位置关系是；

(2)、如图2，当点 $E$ 在菱形 $A B C D$ 外部时，连接 $C E$ ．那么（1）中的结论是否仍成立？若成立，请予以证明；若不成立，请说明理由；

(3)、如图3，当点 $P$ 在线段 $B D$ 的延长线上时，连接 $B E$ ，若 $A B = 4 \sqrt{3}$ ， $B E = 4 \sqrt{19}$ ，请直接写出四边形 $A D P E$ 的面积．

查看试题解析

候选人		甲	乙	丙	丁
测试成绩（百分制）	面试	$86$	$92$	$90$	$83$
测试成绩（百分制）	笔试	$90$	$83$	$83$	$92$

书本类别	A类	B类
进价（单位：元）	18	12
备注	用不超过16800元购进两类图书共1000本，A类图书不少于600本．