山东省潍坊市2023年中考数学真题
试卷更新日期:2023-08-16 类型:中考真卷
一、单选题
-
1. 在实数1,-1,0,中,最大的数是( )A、1 B、-1 C、0 D、2. 下列图形由正多边形和圆弧组成,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 实数a , b , c在数轴上对应的点如图所示,下列判断正确的是( )
3. 实数a , b , c在数轴上对应的点如图所示,下列判断正确的是( ) A、 B、 C、 D、4. 在我国古代建筑中经常使用榫卯构件,如图是某种榫卯构件的示意图,其中,卯的俯视图是( )
A、 B、 C、 D、4. 在我国古代建筑中经常使用榫卯构件,如图是某种榫卯构件的示意图,其中,卯的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,在直角坐标系中,一次函数与反比例函数的图象交于A , B两点,下列结论正确的是( )
5. 如图,在直角坐标系中,一次函数与反比例函数的图象交于A , B两点,下列结论正确的是( )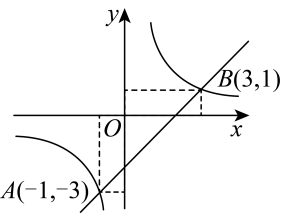 A、当时, B、当时, C、当时, D、当时,6. 如图,在直角坐标系中,菱形的顶点A的坐标为 , . 将菱形沿x轴向右平移1个单位长度,再沿y轴向下平移1个单位长度,得到菱形 , 其中点的坐标为( )
A、当时, B、当时, C、当时, D、当时,6. 如图,在直角坐标系中,菱形的顶点A的坐标为 , . 将菱形沿x轴向右平移1个单位长度,再沿y轴向下平移1个单位长度,得到菱形 , 其中点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
7. 下列运算正确的是( )A、 B、 C、 D、8. 下列命题正确的是( )A、在一个三角形中至少有两个锐角 B、在圆中,垂直于弦的直径平分弦 C、如果两个角互余,那么它们的补角也互余 D、两条直线被第三条直线所截,同位角一定相等9. 已知抛物线经过点 , 则下列结论正确的是( )A、拋物线的开口向下 B、拋物线的对称轴是 C、拋物线与轴有两个交点 D、当时,关于的一元二次方程有实根10. 发动机的曲柄连杆将直线运动转化为圆周运动,图①是发动机的实物剖面图,图②是其示意图.图②中,点A在直线l上往复运动,推动点B做圆周运动形成 , 与表示曲柄连杆的两直杆,点C、D是直线l与的交点;当点A运动到E时,点B到达C;当点A运动到F时,点B到达D . 若 , , 则下列结论正确的是( )

 A、 B、 C、当与相切时, D、当时,
A、 B、 C、当与相切时, D、当时,三、填空题
-
11. 从、 , 中任意选择两个数,分别填在算式里面的“□”与“○”中,计算该算式的结果是 . (只需写出一种结果)12. 用与教材中相同型号的计算器,依次按键
 ,显示结果为
,显示结果为 .借助显示结果,可以将一元二次方程的正数解近似表示为 . (精确到) 13. 投掷两枚骰子,朝上一面的点数之和为7的概率是 .14. 在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,、、在同一平面内,点A、C、E在一条水平直线上.已知米,米,米,米,人从点F远眺塔顶B , 视线恰好经过竹竿的顶端D , 可求出塔的高度.根据以上信息,塔的高度为米.
.借助显示结果,可以将一元二次方程的正数解近似表示为 . (精确到) 13. 投掷两枚骰子,朝上一面的点数之和为7的概率是 .14. 在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,、、在同一平面内,点A、C、E在一条水平直线上.已知米,米,米,米,人从点F远眺塔顶B , 视线恰好经过竹竿的顶端D , 可求出塔的高度.根据以上信息,塔的高度为米.
四、解答题
-
15.(1)、化简:(2)、利用数轴,确定不等式组的解集.16. 如图,在中,平分 , , 重足为点E , 过点E作、交于点F , G为的中点,连接 . 求证: .
 17. 如图,l是南北方向的海岸线,码头A与灯塔B相距24千米,海岛C位于码头A北偏东方向.一艘勘测船从海岛C沿北偏西方向往灯塔B行驶,沿线勘测石油资源,勘测发现位于码头A北偏东方向的D处石油资源丰富.若规划修建从D处到海岸线的输油管道,则输油管道的最短长度是多少千米?(结果保留根号)
17. 如图,l是南北方向的海岸线,码头A与灯塔B相距24千米,海岛C位于码头A北偏东方向.一艘勘测船从海岛C沿北偏西方向往灯塔B行驶,沿线勘测石油资源,勘测发现位于码头A北偏东方向的D处石油资源丰富.若规划修建从D处到海岸线的输油管道,则输油管道的最短长度是多少千米?(结果保留根号) 18. 为研究某种化学试剂的挥发情况,某研究团队在两种不同的场景下做对比实验,收集了该试剂挥发过程中剩余质量y(克)随时间x(分钟)变化的数据(),并分别绘制在直角坐标系中,如下图所示.
18. 为研究某种化学试剂的挥发情况,某研究团队在两种不同的场景下做对比实验,收集了该试剂挥发过程中剩余质量y(克)随时间x(分钟)变化的数据(),并分别绘制在直角坐标系中,如下图所示. (1)、从 , , 中,选择适当的函数模型分别模拟两种场景下随变化的函数关系,并求出相应的函数表达式;(2)、查阅文献可知,该化学试剂发挥作用的最低质量为3克.在上述实验中,该化学试剂在哪种场景下发挥作用的时间更长?19. 某中学积极推进校园文学创作,倡导每名学生每学期向校报编辑部至少投1篇稿件.学期末,学校对七、八年级的学生投稿情况进行调查.
(1)、从 , , 中,选择适当的函数模型分别模拟两种场景下随变化的函数关系,并求出相应的函数表达式;(2)、查阅文献可知,该化学试剂发挥作用的最低质量为3克.在上述实验中,该化学试剂在哪种场景下发挥作用的时间更长?19. 某中学积极推进校园文学创作,倡导每名学生每学期向校报编辑部至少投1篇稿件.学期末,学校对七、八年级的学生投稿情况进行调查.【数据的收集与整理】
分别从两个年级随机抽取相同数量的学生,统计每人在本学期投稿的篇数,制作了频数分布表.
投稿篇数(篇)
1
2
3
4
5
七年级频数(人)
7
10
15
12
6
八年级频数(人)
2
10
13
21
4
【数据的描述与分析】
(1)、求扇形统计图中圆心角的度数,并补全频数直方图. (2)、根据频数分布表分别计算有关统计量:
(2)、根据频数分布表分别计算有关统计量:统计量
中位数
众数
平均数
方差
七年级
3
3
1.48
八年级
m
n
3.3
1.01
直接写出表格中m、n的值,并求出 .
(3)、【数据的应用与评价】从中位数、众数、平均数、方差中,任选两个统计量,对七、八年级学生的投稿情况进行比较,并做出评价.
20. 工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量, , 与之间的距离为2米,米,米, , . , , 是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?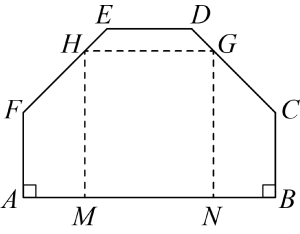 21. 如图,正方形内接于 , 在上取一点E , 连接 , . 过点A作 , 交于点G , 交于点F , 连接 , .
21. 如图,正方形内接于 , 在上取一点E , 连接 , . 过点A作 , 交于点G , 交于点F , 连接 , . (1)、求证:;(2)、若 , , 求阴影部分的面积.22. [材料阅读]
(1)、求证:;(2)、若 , , 求阴影部分的面积.22. [材料阅读]用数形结合的方法,可以探究的值,其中 .
例求的值.
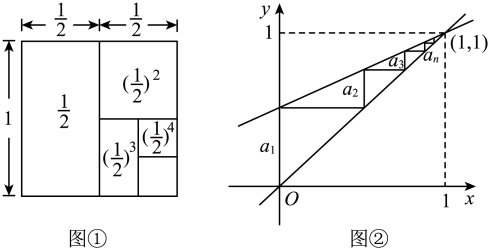
方法1:借助面积为1的正方形,观察图①可知
的结果等于该正方形的面积,
即 .
方法2:借助函数和的图象,观察图②可知
的结果等于 , , , …,…等各条竖直线段的长度之和,
即两个函数图象的交点到轴的距离.因为两个函数图象的交点到轴的距为1,
所以, .


【实践应用】
(1)、任务一 完善的求值过程.方法1:借助面积为2的正方形,观察图③可知 .
方法2:借助函数和的图象,观察图④可知
因为两个函数图象的交点的坐标为 ,
所以, .
(2)、任务二 参照上面的过程,选择合适的方法,求的值.(3)、任务三 用方法2,求的值(结果用表示).(4)、【迁移拓展】长宽之比为的矩形是黄金矩形,将黄金矩形依次截去一个正方形后,得到的新矩形仍是黄金矩形.
观察图⑤,直接写出的值.