山东省济南市2023年中考数学真题

试卷更新日期：2023-08-16 类型：中考真卷

进入出卷网下载

一、单选题

1. 下列几何体中，主视图是三角形的为（　　　）

A、 B、 C、 D、

查看试题解析
2. 2022年我国粮食总产量再创新高，达686530000吨．将数字686530000用科学记数法表示为（　　　）

A、 $0.68653 \times 1 0^{8}$ B、 $6.8653 \times 1 0^{8}$ C、 $6.8653 \times 1 0^{7}$ D、 $68.653 \times 1 0^{7}$

查看试题解析
3. 如图，一块直角三角板的直角顶点放在直尺的一边上．如果 $∠ 1 = 70 °$ ，那么 $∠ 2$ 的度数是（　　）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $45 °$

查看试题解析
4. 实数 $a$ ， $b$ 在数轴上对应点的位置如图所示，则下列结论正确的是（　　　）

A、 $a b > 0$ B、 $a + b > 0$ C、 $a + 3 < b + 3$ D、 $- 3 a < - 3 b$

查看试题解析
5. 下图是度量衡工具汉尺、秦权、新莽铜卡尺和商鞅方升的示意图，其中既是轴对称图形又是中心对称图形的是（　　　）

A、 B、 C、 D、

查看试题解析
6. 下列运算正确的是（　　　）

A、 $a^{2} \cdot a^{4} = a^{8}$ B、 $a^{4} - a^{3} = a$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $a^{4} \div a^{2} = a^{2}$

查看试题解析
7. 已知点 $A (- 4 ， y_{1})$ ， $B (- 2 ， y_{2})$ ， $C (3 ， y_{3})$ 都在反比例函数 $y = \frac{k}{x} (k < 0)$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（　　　）

A、 $y_{3} < y_{2} < y_{1}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析
8. 从甲、乙、丙、丁4名同学中随机抽取2名同学参加图书节志愿服务活动，其中甲同学是女生，乙、丙、丁同学都是男生，被抽到的2名同学都是男生的概率为（　　　）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 36 °$ ，以点 $C$ 为圆心，以 $B C$ 为半径作弧交 $A C$ 于点 $D$ ，再分别以 $B$ ， $D$ 为圆心，以大于 $\frac{1}{2} B D$ 的长为半径作弧，两弧相交于点 $P$ ，作射线 $C P$ 交 $A B$ 于点 $E$ ，连接 $D E$ ．以下结论不正确的是（　　　）

A、 $∠ B C E = 36 °$ B、 $B C = A E$ C、 $\frac{B E}{A C} = \frac{\sqrt{5} - 1}{2}$ D、 $\frac{S_{△ A E C}}{S_{△ B E C}} = \frac{\sqrt{5} + 1}{2}$

查看试题解析
10. 定义：在平面直角坐标系中，对于点 $P (x_{1} ， y_{1})$ ，当点 $Q (x_{2} ， y_{2})$ 满足 $2 (x_{1} + x_{2}) = y_{1} + y_{2}$ 时，称点 $Q (x_{2} ， y_{2})$ 是点 $P (x_{1} ， y_{1})$ 的“倍增点”，已知点 $P_{1} (1 ， 0)$ ，有下列结论：
①点 $Q_{1} (3 ， 8)$ ， $Q_{2} (- 2 ， - 2)$ 都是点 $P_{1}$ 的“倍增点”；
②若直线 $y = x + 2$ 上的点A是点 $P_{1}$ 的“倍增点”，则点 $A$ 的坐标为 $(2 ， 4)$ ；
③抛物线 $y = x^{2} - 2 x - 3$ 上存在两个点是点 $P_{1}$ 的“倍增点”；
④若点 $B$ 是点 $P_{1}$ 的“倍增点”，则 $P_{1} B$ 的最小值是 $\frac{4 \sqrt{5}}{5}$ ．
其中，正确结论的个数是（　　　）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 因式分解: $x^{2} - 16 =$ .

查看试题解析
12. 围棋起源于中国，棋子分黑白两色．一个不透明的盒子中装有3个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑色棋子的概率是 $\frac{1}{4}$ ，则盒子中棋子的总个数是．

查看试题解析
13. 关于 $x$ 的一元二次方程 $x^{2} - 4 x + 2 a = 0$ 有实数根，则 $a$ 的值可以是（写出一个即可）．

查看试题解析
14. 如图，正五边形 $A B C D E$ 的边长为 $2$ ，以 $A$ 为圆心，以 $A B$ 为半径作弧 $B E$ ，则阴影部分的面积为（结果保留 $π$ ）．

查看试题解析
15. 学校提倡“低碳环保，绿色出行”，小明和小亮分别选择步行和骑自行车上学，两人各自从家同时同向出发，沿同一条路匀速前进．如图所示， $l_{1}$ 和 $l_{2}$ 分别表示两人到小亮家的距离 $s (k m)$ 和时间 $t (h)$ 的关系，则出发h后两人相遇．

查看试题解析
16. 如图，将菱形纸片 $A B C D$ 沿过点 $C$ 的直线折叠，使点 $D$ 落在射线 $C A$ 上的点 $E$ 处，折痕 $C P$ 交 $A D$ 于点 $P$ ．若 $∠ A B C = 30 °$ ， $A P = 2$ ，则 $P E$ 的长等于．

查看试题解析

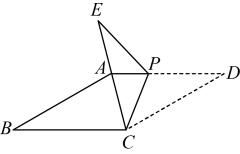
三、解答题

17. 计算： $| - \sqrt{3} | + {(\frac{1}{2})}^{- 1} + {(π + 1)}^{0} - t a n 60 °$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 2 (x + 2) > x + 3 ① \\ \frac{x}{3} < \frac{x + 2}{5} ② \end{array}$ ，并写出它的所有整数解．

查看试题解析
19. 已知：如图，点 $O$ 为 $▱ A B C D$ 对角线 $A C$ 的中点，过点 $O$ 的直线与 $A D$ ， $B C$ 分别相交于点 $E$ ， $F$ ．
求证： $D E = B F$ ．

查看试题解析
20. 图1是某越野车的侧面示意图，折线段 $A B C$ 表示车后盖，已知 $A B = 1 m$ ， $B C = 0.6 m$ ， $∠ A B C = 123 °$ ，该车的高度 $A O = 1.7 m$ ．如图2，打开后备箱，车后盖 $A B C$ 落在 $A B^{^{'}} C^{^{'}}$ 处， $A B^{'}$ 与水平面的夹角 $∠ B^{'} A D = 27 °$ ．

(1)、求打开后备箱后，车后盖最高点 $B^{'}$ 到地面 $l$ 的距离；

(2)、若小琳爸爸的身高为 $1.8 m$ ，他从打开的车后盖 $C^{'}$ 处经过，有没有碰头的危险?请说明理由．
（结果精确到 $0 ． 01 m$ ，参考数据： $s i n 27 ° \approx 0.454$ ， $c o s 27 ° \approx 0.891$ ， $t a n 27 ° \approx 0.510$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
21. 2023年，国内文化和旅游行业复苏势头强劲．某社团对30个地区“五一”假期的出游人数进行了调查，获得了它们“五一”假期出游人数（出游人数用 $m$ 表示，单位：百万）的数据，并对数据进行统计整理．数据分成5组：
A组： $1 \leq m < 12$ ；B组： $12 \leq m < 23$ ；C组： $23 \leq m < 34$ ；D组： $34 \leq m < 45$ ；E组： $45 \leq m < 56$ ．
下面给出了部分信息：
a ． B组的数据：12，13，15，16，17，17，18，20．
b ．不完整的“五一”假期出游人数的频数分布直方图和扇形统计图如下：

请根据以上信息完成下列问题：

(1)、统计图中E组对应扇形的圆心角为度；

(2)、请补全频数分布直方图；

(3)、这30个地区“五一”假期出游人数的中位数是百万；

(4)、各组“五一”假期的平均出游人数如下表：
组别
A $1 \leq m < 12$
B $12 \leq m < 23$
C $23 \leq m < 34$
D $34 \leq m < 45$
E $45 \leq m < 56$
平均出游人数（百万）
5.5
16
32.5
42
50
求这30个地区“五一”假期的平均出游人数．

查看试题解析
22. 如图， $A B$ ， $C D$ 为 $⊙ O$ 的直径， $C$ 为 $⊙ O$ 上一点，过点 $C$ 的切线与 $A B$ 的延长线交于点 $P$ ， $∠ A B C = 2 ∠ B C P$ ，点 $E$ 是 $\overset{⌢}{B D}$ 的中点，弦 $C E$ ， $B D$ 相交于点F．

(1)、求 $∠ O C B$ 的度数；

(2)、若 $E F = 3$ ，求 $⊙ O$ 直径的长．

查看试题解析
23. 某校开设智能机器人编程的校本课程，购买了A ， B两种型号的机器人模型．A型机器人模型单价比B型机器人模型单价多200元，用2000元购买A型机器人模型和用1200元购买B型机器人模型的数量相同．

(1)、求A型，B型机器人模型的单价分别是多少元?

(2)、学校准备再次购买A型和B型机器人模型共40台，购买B型机器人模型不超过A型机器人模型的3倍，且商家给出了两种型号机器人模型均打八折的优惠．问购买A型和B型机器人模型各多少台时花费最少?最少花费是多少元?

查看试题解析
24. 综合与实践
如图1，某兴趣小组计划开垦一个面积为 $8 m^{2}$ 的矩形地块 $A B C D$ 种植农作物，地块一边靠墙，另外三边用木栏围住，木栏总长为 $a m^{2}$ ．

【问题提出】
小组同学提出这样一个问题：若 $a = 10$ ，能否围出矩形地块？

(1)、【问题探究】
小颖尝试从“函数图象”的角度解决这个问题：
设 $A B$ 为 $x m$ ， $B C$ 为 $y m$ ．由矩形地块面积为 $8 m^{2}$ ，得到 $x y = 8$ ，满足条件的 $(x ， y)$ 可看成是反比例函数 $y = \frac{8}{x}$ 的图象在第一象限内点的坐标；木栏总长为 $10 m$ ，得到 $2 x + y = 10$ ，满足条件的 $(x ， y)$ 可看成一次函数 $y = - 2 x + 10$ 的图象在第一象限内点的坐标，同时满足这两个条件的 $(x ， y)$ 就可以看成两个函数图象交点的坐标．
如图2，反比例函数 $y = \frac{8}{x} (x > 0)$ 的图象与直线 $l_{1}$ ： $y = - 2 x + 10$ 的交点坐标为 $(1 ， 8)$ 和，因此，木栏总长为 $10 m$ 时，能围出矩形地块，分别为： $A B = 1 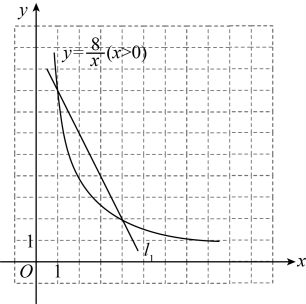m$ ， $B C = 8 m$ ；或 $A B =$ m ， $B C =$ m ．

根据小颖的分析思路，完成上面的填空．

(2)、【类比探究】
若 $a = 6$ ，能否围出矩形地块？请仿照小颖的方法，在图2中画出一次函数图象并说明理由．

(3)、【问题延伸】
当木栏总长为 $a m$ 时，小颖建立了一次函数 $y = - 2 x + a$ ．发现直线 $y = - 2 x + a$ 可以看成是直线 $y = - 2 x$ 通过平移得到的，在平移过程中，当过点 $(2 ， 4)$ 时，直线 $y = - 2 x + a$ 与反比例函数 $y = \frac{8}{x} (x > 0)$ 的图象有唯一交点．
请在图2中画出直线 $y = - 2 x + a$ 过点 $(2 ， 4)$ 时的图象，并求出 $a$ 的值．

(4)、【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“ $y = - 2 x + a$ 与 $y = \frac{8}{x}$ 图象在第一象限内交点的存在问题”．
若要围出满足条件的矩形地块，且 $A B$ 和 $B C$ 的长均不小于 $1 m$ ，请直接写出 $a$ 的取值范围．

查看试题解析
25. 在平面直角坐标系 $x O y$ 中，正方形 $A B C D$ 的顶点 $A$ ， $B$ 在 $x$ 轴上， $C (2 ， 3)$ ， $D (- 1 ， 3)$ ．抛物线 $y = a x^{2} - 2 a x + c (a < 0)$ 与 $x$ 轴交于点 $E (- 2 ， 0)$ 和点 $F$ ．

(1)、如图1，若抛物线过点 $C$ ，求抛物线的表达式和点 $F$ 的坐标；

(2)、如图2，在（1）的条件下，连接 $C F$ ，作直线 $C E$ ，平移线段 $C F$ ，使点 $C$ 的对应点 $P$ 落在直线 $C E$ 上，点 $F$ 的对应点 $Q$ 落在抛物线上，求点 $Q$ 的坐标；

(3)、若抛物线 $y = a x^{2} - 2 a x + c (a < 0)$ 与正方形 $A B C D$ 恰有两个交点，求 $a$ 的取值范围．

查看试题解析
26. 在矩形 $A B C D$ 中， $A B = 2$ ， $A D = 2 \sqrt{3}$ ，点 $E$ 在边 $B C$ 上，将射线 $A E$ 绕点 $A$ 逆时针旋转90°，交 $C D$ 延长线于点 $G$ ，以线段 $A E$ ， $A G$ 为邻边作矩形 $A E F G$ ．

(1)、如图1，连接 $B D$ ，求 $∠ B D C$ 的度数和 $\frac{D G}{B E}$ 的值；

(2)、如图2，当点 $F$ 在射线 $B D$ 上时，求线段 $B E$ 的长；

(3)、如图3，当 $E A = E C$ 时，在平面内有一动点 $P$ ，满足 $P E = E F$ ，连接 $P A$ ， $P C$ ，求 $P A + P C$ 的最小值．

查看试题解析

组别	A $1 \leq m < 12$	B $12 \leq m < 23$	C $23 \leq m < 34$	D $34 \leq m < 45$	E $45 \leq m < 56$
平均出游人数（百万）	5.5	16	32.5	42	50