湖南省娄底市2023年中考数学真题

试卷更新日期：2023-08-16 类型：中考真卷

进入出卷网下载

一、单选题

1. $2023$ 的倒数是（）

A、 $2023$ B、 $\frac{1}{2023}$ C、 $- \frac{1}{2023}$ D、 $- 2023$

查看试题解析
2. 下列运算正确的是（）

A、 $a^{2} \cdot a^{4} = a^{8}$ B、 $a^{2} + 3 a = 4 a^{2}$ C、 $(a + 2) (a - 2) = a^{2} - 2$ D、 ${(- 2 a^{2} b)}^{3} = - 8 a^{6} b^{3}$

查看试题解析
3. 新时代我国教育事业取得了历史性成就，目前我国已建成世界上规模最大的教育体系，教育现代化发展总体水平跨入世界中上国家行列，其中高等教育在学总规模达到4430万人，处于高等教育普及化阶段.4430万用科学记数法表示为（）

A、 $443 \times 1 0^{5}$ B、 $4.43 \times 1 0^{7}$ C、 $4.43 \times 1 0^{8}$ D、 $0.443 \times 1 0^{8}$

查看试题解析
4. 一个小组7名同学的身高（单位： $c m$ ）分别为：175，160，158，155，168，151，170．这组数据的中位数是（）

A、151 B、155 C、158 D、160

查看试题解析
5. 不等式组 ${\begin{array}{l} - x + 3 < 5 \\ 2 x - 2 \leq 0 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 将直线 $y = 2 x + 1$ 向右平移2个单位所得直线的表达式为（）

A、 $y = 2 x - 1$ B、 $y = 2 x - 3$ C、 $y = 2 x + 3$ D、 $y = 2 x + 5$

查看试题解析
7. 从 $\frac{36}{7}$ ， 3.1415926， $3 . \dot{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ ， $- \sqrt[3]{8}$ ， $\sqrt[3]{9}$ 中随机抽取一个数，此数是无理数的概率是（）

A、 $\frac{2}{7}$ B、 $\frac{3}{7}$ C、 $\frac{4}{7}$ D、 $\frac{5}{7}$

查看试题解析
8. 一个长方体物体的一顶点所在A、B、C三个面的面积比是 $3 ： 2 ： 1$ ，如果分别按A、B、C面朝上将此物体放在水平地面上，地面所受的压力产生的压强分别为 $P_{A}$ 、 $P_{B}$ 、 $P_{C}$ （压强的计算公式为 $P = \frac{F}{S}$ ），则 $P_{A} ： P_{B} ： P_{C} =$ （）

A、 $2 ： 3 ： 6$ B、 $6 ： 3 ： 2$ C、 $1 ： 2 ： 3$ D、 $3 ： 2 ： 1$

查看试题解析
9. 如图，正六边形 $A B C D E F$ 的外接圆 $⊙ O$ 的半径为2，过圆心O的两条直线 $l_{1}$ 、 $l_{2}$ 的夹角为 $60 °$ ，则图中的阴影部分的面积为（）

A、 $\frac{4}{3} π - \sqrt{3}$ B、 $\frac{4}{3} π - \frac{\sqrt{3}}{2}$ C、 $\frac{2}{3} π - \sqrt{3}$ D、 $\frac{2}{3} π - \frac{\sqrt{3}}{2}$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，给出下列结论：① $a b c < 0$ ；② $4 a - 2 b + c > 0$ ；③ $a - b > m (a m + b)$ （m为任意实数）；④若点 $(- 3 ， y_{1})$ 和点 $(3 ， y_{2})$ 在该图象上，则 $y_{1} > y_{2}$ ．其中正确的结论是（）

A、①② B、①④ C、②③ D、②④

查看试题解析
11. 从n个不同元素中取出 $m (m \leq n)$ 个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数，用符号 $C_{n}^{m}$ 表示， $C_{n}^{m} = \frac{n (n - 1) (n - 2) \cdot \cdot \cdot (n - m + 1)}{m (m - 1) \cdot \cdot \cdot 1}$ （ $n \geq m$ ， n、m为正整数）；例如： $C_{5}^{2} = \frac{5 \times 4}{2 \times 1}$ ， $C_{8}^{3} = \frac{8 \times 7 \times 6}{3 \times 2 \times 1}$ ，则 $C_{9}^{4} + C_{9}^{5} =$ （）

A、 $C_{9}^{6}$ B、 $C_{10}^{4}$ C、 $C_{10}^{5}$ D、 $C_{10}^{6}$

查看试题解析
12. 我国南宋著名数学家秦九韶在他的著作《数学九章》一书中，给出了这样的一个结论：三边分别为a、b、c的 $△ A B C$ 的面积为 $S_{△ A B C} = \frac{1}{2} \sqrt{a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}}$ ． $△ A B C$ 的边a、b、c所对的角分别是∠A、∠B、∠C，则 $S_{△ A B C} = \frac{1}{2} a b s i n C = \frac{1}{2} a c s i n B = \frac{1}{2} b c s i n A$ ．下列结论中正确的是（）

A、 $c o s C = \frac{a^{2} + b^{2} - c^{2}}{2 a b}$ B、 $c o s C = - \frac{a^{2} + b^{2} - c^{2}}{2 a b}$ C、 $c o s C = \frac{a^{2} + b^{2} - c^{2}}{2 a c}$ D、 $c o s C = \frac{a^{2} + b^{2} - c^{2}}{2 b c}$

查看试题解析

二、填空题

13. 函数 $y = \sqrt{x + 1}$ 的自变量x的取值范围为．

查看试题解析
14. 若m是方程 $x^{2} - 2 x - 1 = 0$ 的根，则 $m^{2} + \frac{1}{m^{2}} =$ ．

查看试题解析
15. 如图，点E在矩形 $A B C D$ 的边 $C D$ 上，将 $△ A D E$ 沿 $A E$ 折叠，点D恰好落在边 $B C$ 上的点F处，若 $B C = 10$ ． $s i n ∠ A F B = \frac{4}{5}$ ，则 $D E =$ ．

查看试题解析
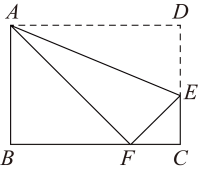16. 如图，在 $△ A B C$ 中， $A C = 3$ ， $A B = 4$ ， $B C$ 边上的高 $A D = 2$ ，将 $△ A B C$ 绕着 $B C$ 所在的直线旋转一周得到的几何体的表面积为．

查看试题解析
17. 如图，抛物线 $y = a x^{2} + b x + c$ 与x轴相交于点 $A (1 ， 0)$ 、点 $B (3 ， 0)$ ，与y轴相交于点C ，点D在抛物线上，当 $C D ∥ x$ 轴时， $C D =$ ．

查看试题解析
18. 若干个同学参加课后社团——舞蹈活动，一次排练中，先到的n个同学均匀排成一个以O点为圆心，r为半径的圆圈（每个同学对应圆周上一个点），又来了两个同学，先到的同学都沿各自所在半径往后移a米，再左右调整位置，使这 $(n + 2)$ 个同学之间的距离与原来n个同学之间的距离（即在圆周上两人之间的圆弧的长）相等．这 $(n + 2)$ 个同学排成圆圈后，又有一个同学要加入队伍，重复前面的操作，则每人须往后移米（请用关于a的代数式表示），才能使得这 $(n + 3)$ 个同学之间的距离与原来n个同学之间的距离相等．

查看试题解析

三、解答题

19. 计算： ${(π - 2023)}^{0} + | 1 - \sqrt{3} | + \sqrt{8} - t a n 60 °$ ．

查看试题解析
20. 先化简，再求值： $(\frac{x}{x + 1} - \frac{2}{x - 1}) \div \frac{1}{x^{2} - 1}$ ，其中x满足 $x^{2} - 3 x - 4 = 0$ ．

查看试题解析
21. 某区教育局为了了解某年级学生对科学知识的掌握情况，在全区范围内随机抽取若干名学生进行科学知识测试，按照测试成绩分优秀、良好、合格与不合格四个等级，并绘制了如下两幅不完整统计图．

(1)、参与本次测试的学生人数为， $m =$ ．

(2)、请补全条形统计图．

(3)、若全区该年纪共有5000名学生，请估计该年级对科学知识掌握情况较好（测试成绩能达到良好及以上等级）的学生人数．

查看试题解析
22. 几位同学在老师的指导下到某景区进行户外实践活动，在登山途中发现该景区某两座山之间风景优美，但路陡难行，为了便于建议景区管理处在这两山顶间建观光索道，他们分别在两山顶上取A、B两点，并过点B架设一水平线型轨道 $C D$ （如图所示），使得 $∠ A B C = α$ ，从点B出发按 $C D$ 方向前进20米到达点E ，即 $B E = 20$ 米，测得 $∠ A E B = β$ ．已知 $s i n α = \frac{24}{25}$ ， $t a n β = 3$ ，求A、B两点间的距离．

查看试题解析
23. 为落实“五育并举”，绿化美化环境，学校在劳动周组织学生到校园周边种植甲、乙两种树苗．已知购买甲种树苗3棵，乙种树苗2棵共需12元；购买甲种树苗1棵，乙种树苗3棵共需11元．

(1)、求每棵甲、乙树苗的价格．

(2)、本次活动共种植了200棵甲、乙树苗，假设所种的树苗若干年后全部长成了参天大树，并且平均每棵树的价值（含生态价值，经济价值）均为原来树苗价的100倍，要想获得不低于5万元的价值，请问乙种树苗种植数量不得少于多少棵？

查看试题解析
24. 如图1，点 $G$ 为等边 $△ A B C$ 的重心，点 $D$ 为 $B C$ 边的中点，连接 $G D$ 并延长至点 $O$ ，使得 $D O = D G$ ，连接 $G B$ ， $G C$ ， $O B$ ， $O C$

(1)、求证：四边形 $B O C G$ 为菱形．

(2)、如图2，以 $O$ 点为圆心， $O G$ 为半径作 $⊙ O$
①判断直线 $A B$ 与 $⊙ O$ 的位置关系，并予以证明．
②点 $M$ 为劣弧 $B C$ 上一动点（与点 $B$ 、点 $C$ 不重合），连接 $B M$ 并延长交 $A C$ 于点 $E$ ，连接 $C M$ 并延长交 $A B$ 于点 $F$ ，求证： $A E + A F$ 为定值．

查看试题解析
25. 鲜艳的中华人民共和国国旗始终是当代中华儿女永不褪色的信仰，国旗上的每颗星都是标准五角星．为了增强学生的国家荣誉感、民族自豪感等．数学老师组织学生对五角星进行了较深入的研究．延长正五边形的各边直到不相邻的边相交，得到一个标准五角星．如图，正五边形 $A B C D E$ 的边 $B A 、 D E$ 的延长线相交于点F ， $∠ E A F$ 的平分线交 $E F$ 于点M ．

(1)、求证： $A E^{2} = E F \cdot E M$ ．

(2)、若 $A F = 1$ ，求 $A E$ 的长．

(3)、求 $\frac{S_{正五边形 A B C D E}}{S_{△ A E F}}$ 的值．

查看试题解析
26. 如图，抛物线 $y = x^{2} + b x + c$ 过点 $A (- 1 ， 0)$ 、点 $B (5 ， 0)$ ，交y轴于点C ．

(1)、求b ， c的值．

(2)、点 $P (x_{0} ， y_{0}) (0 < x_{0} < 5)$ 是抛物线上的动点
①当 $x_{0}$ 取何值时， $△ P B C$ 的面积最大？并求出 $△ P B C$ 面积的最大值；
②过点P作 $P E ⊥ x$ 轴，交 $B C$ 于点E ，再过点P作 $P F ∥ x$ 轴，交抛物线于点F ，连接 $E F$ ，问：是否存在点P ，使 $△ P E F$ 为等腰直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析