【备考2024】高考数学(代数版块)细点逐一突破复习专练:Venn图表达集合的关系及运算
试卷更新日期:2023-08-15 类型:二轮复习
一、选择题
-
1. 如图所示的Venn图中,、是非空集合,定义集合为阴影部分表示的集合.若 , , 则( )
 A、 B、 C、 D、2. 已知集合 , 则下列Venn图中阴影部分可以表示集合的是( )A、
A、 B、 C、 D、2. 已知集合 , 则下列Venn图中阴影部分可以表示集合的是( )A、 B、
B、 C、
C、 D、
D、 3. 已知全集 , 集合 , , 则下图阴影部分所对应的集合为( )
3. 已知全集 , 集合 , , 则下图阴影部分所对应的集合为( ) A、 B、 C、或 D、4. 已知P,Q为R的两个非空真子集,若 , 则下列结论正确的是( )A、 , B、 , C、 , D、 ,5. 设全集 , 集合 , , 则下面Venn图中阴影部分表示的集合是( )
A、 B、 C、或 D、4. 已知P,Q为R的两个非空真子集,若 , 则下列结论正确的是( )A、 , B、 , C、 , D、 ,5. 设全集 , 集合 , , 则下面Venn图中阴影部分表示的集合是( ) A、 B、 C、 D、6. 已知 , 为R的两个不相等的非空子集,若 , 则( )A、 B、 C、 D、7. 已知全集 , 集合 , 集合 , 用如图所示的阴影部分表示的集合为( )
A、 B、 C、 D、6. 已知 , 为R的两个不相等的非空子集,若 , 则( )A、 B、 C、 D、7. 已知全集 , 集合 , 集合 , 用如图所示的阴影部分表示的集合为( ) A、{2,4} B、{0,3,5,6} C、{0,2,3,4,5,6} D、{1,2,4}8. 已知全集 , 集合 , 若图中阴影部分表示的集合是 , 则集合( )
A、{2,4} B、{0,3,5,6} C、{0,2,3,4,5,6} D、{1,2,4}8. 已知全集 , 集合 , 若图中阴影部分表示的集合是 , 则集合( ) A、 B、 C、 D、9. 已知非空集合A,B满足以下两个条件:(1) , ;(2)A的元素个数不是A中的元素,B的元素个数不是B中的元素.则有序集合对的个数为( )A、1 B、2 C、3 D、410. 已知集合 , , 则如图所示的阴影部分表示的集合为( )
A、 B、 C、 D、9. 已知非空集合A,B满足以下两个条件:(1) , ;(2)A的元素个数不是A中的元素,B的元素个数不是B中的元素.则有序集合对的个数为( )A、1 B、2 C、3 D、410. 已知集合 , , 则如图所示的阴影部分表示的集合为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 设函数f(x)= ,集合A={x|y=f(x)},B={y|y=f(x)},则如图中阴影部分表示的集合为 .
 12. 某班有学生45人,参加了数学小组的学生有31人,参加了英语小组的学生有26人.已知该班每个学生都至少参加了这两个小组中的一个小组,则该班学生中既参加了数学小组,又参加了英语小组的学生有人.13. 已知集合 , 集合 , 则Venn图中阴影部分表示的集合中元素的个数为 .
12. 某班有学生45人,参加了数学小组的学生有31人,参加了英语小组的学生有26人.已知该班每个学生都至少参加了这两个小组中的一个小组,则该班学生中既参加了数学小组,又参加了英语小组的学生有人.13. 已知集合 , 集合 , 则Venn图中阴影部分表示的集合中元素的个数为 . 14. 某单位工会组织75名会员观看《光荣与梦想》、《觉醒年代》、《跨过鸭绿江》三部建党百年优秀电视,对这三部剧的观看情况统计如下:
14. 某单位工会组织75名会员观看《光荣与梦想》、《觉醒年代》、《跨过鸭绿江》三部建党百年优秀电视,对这三部剧的观看情况统计如下:观看情况
观看人数
只看过《光荣与梦想》
12
只看过《觉醒年代》
11
只看过《跨过鸭绿江》
8
只看过《光荣与梦想》和《觉醒年代》
7
只看过《光荣与梦想》和《跨过鸭绿江》
4
只看过《觉醒年代》和《跨过鸭绿江》
5
同时看过《光荣与梦想》、《觉醒年代》和《跨过鸭绿江》
21
则会员中看过《跨过鸭绿江》的共有人,三部电视剧中,看过至少一部的有人.
15. 某中学的学生积极参加体育锻炼,其中有75%的学生喜欢足球或游泳,56%的学生喜欢足球,38%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是.16. 已知集合 ,集合 , ,则下图中阴影部分所表示的集合为 . 17. 已知全集 ,集合 ,则图中阴影部分所表示的集合为.
17. 已知全集 ,集合 ,则图中阴影部分所表示的集合为.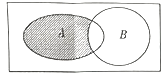 18. 学校先举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,该班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有名同学参赛.19.
18. 学校先举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,该班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有名同学参赛.19.已知不等式|x﹣2|<3的解集为 A,函数y=ln(1﹣x)的定义域为B,则图中阴影部分表示的集合为 .

三、解答题
-
20. 为了研究55岁左右的中国人睡眠质量与心脑血管病是否有关联,某机构在适龄人群中随机抽取了100万个样本,调查了他们每周是否至少三个晚上出现了三种失眠症状, 症状:入睡困难; 症状:醒得太早; 症状:不能深度入睡或做梦,得到的调查数据如下:
数据1:出现 症状人数为8.5万,出现 症状人数为9.3万,出现 症状人数为6.5万,其中含 症状同时出现1.8万人, 症状同时出现1万人, 症状同时出现2万人, 症状同时出现0.5万人;
数据2:同时有失眠症状和患心脑血管病的人数为5万人,没有失眠症状且无心脑血管病的人数为73万人.
(Ⅰ)依据上述数据试分析55岁左右的中国人患有失眠症的比例大约多少?
(Ⅱ)根据以上数据完成如下列联表,并根据所填列联表判断能否有95%的把握说明失眠与心脑血管病存在“强关联”?
失眠
不失眠
合计
患心脑血管疾病
不患心脑血管疾病
合计
参考数据如下:
0.50
0.40
0.25
0.15
0.10
0.455
0.708
1.323
2.072
2.706
0.05
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
参考公式:
21. 随着人们生活水平的日益提高,人们对孩子的培养也愈发重视,各种兴趣班如雨后春笋般出现在我们日常生活中.据调查,3~6岁的幼儿大部分参加的是艺术类,其中舞蹈和绘画比例最大,就参加兴趣班的男女比例而言,女生参加兴趣班的比例远远超过男生.随机调查了某区100名3~6岁幼儿在一年内参加舞蹈或绘画兴趣班的情况,得到如下表格:不参加舞蹈且不参
加绘画兴趣班
参加舞蹈不参加
绘画兴趣班
参加绘画不参加
舞蹈兴趣班
参加舞蹈且参加
绘画兴趣班
人数
14
35
26
25
(Ⅰ)估计该区3~6岁幼儿参加舞蹈兴趣班的概率;
(Ⅱ)通过所调查的100名3~6岁幼儿参加兴趣班的情况,填写下面列联表,并根据列联表判断是否有99.9%的把握认为参加舞蹈兴趣班与性别有关.
参加舞蹈兴趣班
不参加舞蹈兴趣班
总计
男生
10
女生
70
总计
附: .
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
22. 已知全集U=R,集合A= ,B={y|y=log2x,4<x<16}, (1)、求图中阴影部分表示的集合C;(2)、若非空集合D={x|4﹣a<x<a},且D⊆(A∪B),求实数a的取值范围.23. 已知 , .
(1)、求图中阴影部分表示的集合C;(2)、若非空集合D={x|4﹣a<x<a},且D⊆(A∪B),求实数a的取值范围.23. 已知 , .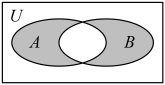 (1)、求 , ;(2)、求图中阴影部分表示的集合.24. 已知集合 , .(1)、若 , 求图中阴影部分;
(1)、求 , ;(2)、求图中阴影部分表示的集合.24. 已知集合 , .(1)、若 , 求图中阴影部分; (2)、若 , 求实数的取值范围.25. 已知全集 ,集合 .
(2)、若 , 求实数的取值范围.25. 已知全集 ,集合 . (1)、求 ;(2)、求如图阴影部分表示的集合.26. 已知全集U={1,2,3,4,5,6,7,8,9},A∩(∁UB)={1,3,5,7},∁U(A∪B)={9},求集合B.
(1)、求 ;(2)、求如图阴影部分表示的集合.26. 已知全集U={1,2,3,4,5,6,7,8,9},A∩(∁UB)={1,3,5,7},∁U(A∪B)={9},求集合B.
