广东省肇庆市广宁县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-15 类型:期末考试
一、单选题
-
1. 下列根式中,最简二次根式的是( )A、 B、 C、 D、2. 若二次根式有意义,则的取值范围是( )A、 B、 C、 D、3. 下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )A、 , , B、1, , C、6,7,8 D、2,3,44. 四边形中, . 要判别四边形是平行四边形,还需满足条件( )
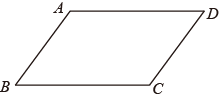 A、 B、 C、 D、5. 一次函数的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )
A、 B、 C、 D、5. 一次函数的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )时间/小时
7
8
9
10
人数
6
9
11
4
A、9,8.5 B、9,9 C、10,9 D、11,8.57. 两个一次函数和在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 下列命题中,是真命题的是()A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形9. 两张全等的矩形纸片 , 按如图的方式叠放在一起, . 若 , , 则图中重叠(阴影)部分的面积为( )
8. 下列命题中,是真命题的是()A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形9. 两张全等的矩形纸片 , 按如图的方式叠放在一起, . 若 , , 则图中重叠(阴影)部分的面积为( ) A、15 B、14 C、13 D、1210. 点P从某四边形的一个顶点A出发,沿着该四边形的边逆时针匀速运动一周.设点P运动的时间为x,点P与该四边形对角线交点的距离为y,表示y与x的函数关系的大致图像如图所示,则该四边形可能是( )
A、15 B、14 C、13 D、1210. 点P从某四边形的一个顶点A出发,沿着该四边形的边逆时针匀速运动一周.设点P运动的时间为x,点P与该四边形对角线交点的距离为y,表示y与x的函数关系的大致图像如图所示,则该四边形可能是( )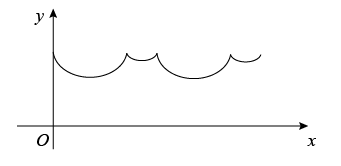 A、
A、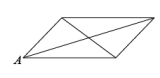 B、
B、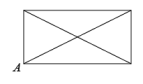 C、
C、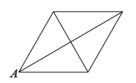 D、
D、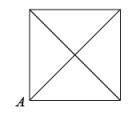
二、填空题
-
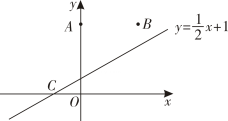
11. 计算:( )2=。12. 如图,在平面直角坐标系中,已知点 , , 直线上有一动点 , 当时,点的坐标是 .
 13. 已知某校女子田径队23人年龄的平均数是13岁,但是后来发现其中一位同学的年龄登记出现错误,将14岁写成了15岁,经重新计算后,正确的平均数为a岁,则a13(在横线上填上“>”或“=”或“<”).14. 如图,在矩形ABCD中,AD=13,AB=5,E为BC上一点,DE平分∠AEC,则CE的长为 .
13. 已知某校女子田径队23人年龄的平均数是13岁,但是后来发现其中一位同学的年龄登记出现错误,将14岁写成了15岁,经重新计算后,正确的平均数为a岁,则a13(在横线上填上“>”或“=”或“<”).14. 如图,在矩形ABCD中,AD=13,AB=5,E为BC上一点,DE平分∠AEC,则CE的长为 . 15. 如图正方形 ABCD 中,E 是 BC 边的中点,将△ABE 沿 AE 对折至△AFE,延长 EF 交 CD 于 G,接 CF,AG.下列结论:① AE∥FC;②∠EAG=45°,且BE+DG=EG;③ ;④ AD=3DG,正确的是(填序号).
15. 如图正方形 ABCD 中,E 是 BC 边的中点,将△ABE 沿 AE 对折至△AFE,延长 EF 交 CD 于 G,接 CF,AG.下列结论:① AE∥FC;②∠EAG=45°,且BE+DG=EG;③ ;④ AD=3DG,正确的是(填序号).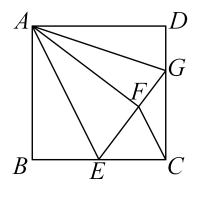
三、解答题
-
16. 计算: .17. 小明想测量学校旗杆的高度,他采用如下的方法:先降旗杆上的绳子接长一些,让它垂到地面还多1米,然后将绳子下端拉直,使它刚好接触地面,测得绳下端离旗杆底部5米,你能帮它计算一下旗杆的高度.
 18. 已知一次函数的图象过点与 .(1)、求这个一次函数的解析式;(2)、求一次函数图象与坐标轴围成的三角形的周长.19. 某公司随机抽取18名销售员,他们的月销售额(单位:万元),数据如下:
18. 已知一次函数的图象过点与 .(1)、求这个一次函数的解析式;(2)、求一次函数图象与坐标轴围成的三角形的周长.19. 某公司随机抽取18名销售员,他们的月销售额(单位:万元),数据如下:25,26,24,22,18,23,22,27,25,21,21,24,35,39,36,35,41,47.
公司根据月销售额情况将销售员分为A,B,C,D四个等级,具体如表:
月销售额(万元)
x≥40
30≤x<40
20≤x<30
x<20
等级
A
B
C
D
请根据以上数据回答下面问题:
(1)、若该公司共有180名销售员,试估计全公司A等级的销售员的人数;(2)、为了调动工作积极性,公司决定对销售员进行奖励:A等级的每人奖励14万元,B等级的每人奖励10万元,C等级的每人奖励8万元,D等级的每人奖励6万元,求这18位销售员获得的平均奖励为多少万元?20. 湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.
求:
(1)、两棵景观树之间的距离;(2)、点B到直线AC的距离.21. 如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE//AB,BE=AF. (1)、求证:四边形ADEF是平行四边形;(2)、若∠ABC=60°,BD=4,求平行四边形ADEF的面积.22. 如图,直线的函数解析式为 , 且与轴交于点 , 直线经过点、 , 直线交于点C.
(1)、求证:四边形ADEF是平行四边形;(2)、若∠ABC=60°,BD=4,求平行四边形ADEF的面积.22. 如图,直线的函数解析式为 , 且与轴交于点 , 直线经过点、 , 直线交于点C. (1)、求直线的函数解析式;(2)、求的面积;(3)、在直线上是否存在点P,使得面积是面积的倍?如果存在,请求出坐标;如果不存在,请说明理由.23. 如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=-x+b与x轴交于点A,且经过定点B(-1,5),直线l1与l2交于点C(2,m).
(1)、求直线的函数解析式;(2)、求的面积;(3)、在直线上是否存在点P,使得面积是面积的倍?如果存在,请求出坐标;如果不存在,请说明理由.23. 如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=-x+b与x轴交于点A,且经过定点B(-1,5),直线l1与l2交于点C(2,m). (1)、求k、b和m的值;(2)、求△ADC的面积;(3)、在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;(4)、若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
(1)、求k、b和m的值;(2)、求△ADC的面积;(3)、在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;(4)、若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.