广东省汕尾市2022-2023学年八年级下学期数学试题
试卷更新日期:2023-08-15 类型:期末考试
一、单选题
-
1. 式子在实数范围内有意义,则x的值可以是( )A、 B、0 C、1 D、62. 下列长度的三条线段能组成直角三角形的是( )A、 B、 C、 D、3. 如图,平行四边形中, , 则等于( ).
 A、120° B、110° C、70° D、30°4. 已知 , 则x的值是( )A、 B、2 C、 D、5. 下列函数图象中,有可能是一次函数图象的是( )A、
A、120° B、110° C、70° D、30°4. 已知 , 则x的值是( )A、 B、2 C、 D、5. 下列函数图象中,有可能是一次函数图象的是( )A、 B、
B、 C、
C、 D、
D、 6. 某中学决定从甲、乙、丙、丁四名初三学生中选出一人参加汕尾市 年数学能力竞赛活动,特统计了他们最近次数学考试成绩,其中,他们的平均成绩都为分,方差分别是 , , , , 该学校派遣( )参加比赛最为合适.A、甲 B、乙 C、丙 D、丁7. 估计 的值在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间8. 将正比例函数的图象向下平移2个单位长度,平移后图象的解析式为( )A、 B、 C、 D、9. 如图,在正方形方格中,每个小正方形的边长都为1,则是( )
6. 某中学决定从甲、乙、丙、丁四名初三学生中选出一人参加汕尾市 年数学能力竞赛活动,特统计了他们最近次数学考试成绩,其中,他们的平均成绩都为分,方差分别是 , , , , 该学校派遣( )参加比赛最为合适.A、甲 B、乙 C、丙 D、丁7. 估计 的值在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间8. 将正比例函数的图象向下平移2个单位长度,平移后图象的解析式为( )A、 B、 C、 D、9. 如图,在正方形方格中,每个小正方形的边长都为1,则是( ) A、锐角 B、直角 C、钝角 D、无法确定10. 如图,矩形中, , , 把矩形沿对角线所在直线折叠,使点落在点处,交于点 , 连接 . 则以下结论:① , ② , ③ , ④是等腰三角形,其中正确的个数是( )
A、锐角 B、直角 C、钝角 D、无法确定10. 如图,矩形中, , , 把矩形沿对角线所在直线折叠,使点落在点处,交于点 , 连接 . 则以下结论:① , ② , ③ , ④是等腰三角形,其中正确的个数是( )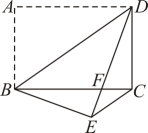 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 化简:= .
12. 如下图,矩形ABCD中,对角线AC,BD相交于点O,OA=4,则BD=.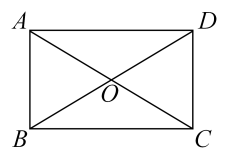 13. 已知一次函数的图象与轴相交于点 , 与轴相交于点 , 则关于的方程的解是 .
13. 已知一次函数的图象与轴相交于点 , 与轴相交于点 , 则关于的方程的解是 . 14. 将长为10,宽为6的矩形分割成四个全等的直角三角形(如图1),拼成“赵爽弦图”(如图2),得到大小两个正方形.则小正方形的面积是 .
14. 将长为10,宽为6的矩形分割成四个全等的直角三角形(如图1),拼成“赵爽弦图”(如图2),得到大小两个正方形.则小正方形的面积是 . 15. 如图,已知平面直角坐标系中有一点 , 且一次函数与x轴相交于点B,与y轴相交于点C,在直线上存在一动点M,连接 , , 当点M运动到最短时,的长度是 .
15. 如图,已知平面直角坐标系中有一点 , 且一次函数与x轴相交于点B,与y轴相交于点C,在直线上存在一动点M,连接 , , 当点M运动到最短时,的长度是 .
三、解答题
-
16. 计算:17. 求值:已知 , 求的值18.
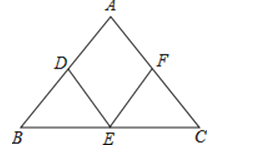
如图,点D、E、F分别是△ABC各边中点.求证:四边形ADEF是平行四边形.
 19. 近几年我市水资源缺乏现象日益凸显,为了加强居民的节水意识,我市制订了每月用水10吨以内(包括10吨)和用水10吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的一次函数,其函数图象如图所示.
19. 近几年我市水资源缺乏现象日益凸显,为了加强居民的节水意识,我市制订了每月用水10吨以内(包括10吨)和用水10吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的一次函数,其函数图象如图所示. (1)、请求出时y与x的函数关系式;(2)、若某用户该月交水费60元,求该户用了多少吨水.20. 如图1,在平行四边形中,点E,F分别在线段 , 上,且 , 连接 , 交于点O.
(1)、请求出时y与x的函数关系式;(2)、若某用户该月交水费60元,求该户用了多少吨水.20. 如图1,在平行四边形中,点E,F分别在线段 , 上,且 , 连接 , 交于点O. (1)、求证:;(2)、连接 , (如图2),若 , 求证:四边形是菱形.21. 年月,“逐梦寰宇问苍穹”中国载人航天工程年成就展在国家博物馆成功举办,标志着我国载人航天工程正式进入空间站应用与发展阶段.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取名学生进行测试,对成绩(百分制)进行整理、描述和分析,成绩划分为(),(),(),()四个等级,并制作出不完整的统计图如下,
(1)、求证:;(2)、连接 , (如图2),若 , 求证:四边形是菱形.21. 年月,“逐梦寰宇问苍穹”中国载人航天工程年成就展在国家博物馆成功举办,标志着我国载人航天工程正式进入空间站应用与发展阶段.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取名学生进行测试,对成绩(百分制)进行整理、描述和分析,成绩划分为(),(),(),()四个等级,并制作出不完整的统计图如下,
根据以上信息,回答下列问题:
(1)、填空: ,(2)、补全条形统计图;(3)、这所学校共有名学生,若全部参加这次测试,请你估计成绩在分以上(含分)的学生人数.

