广东省肇庆市广宁县2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-08-15 类型:期末考试
一、单选题
-
1. 在实数-2, , 0,中,最小的数是( )A、 B、0 C、 D、-22. 在平面直角坐标系中,点P(﹣3,﹣4)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图,直线a、b被直线c所截,若 , , 则等于( )
 A、 B、 C、 D、4. 下列调查中,调查方式选择合理的是( )A、为了了解某一批灯泡的寿命,选择全面调查 B、为了了解一批袋装食品是否含有防腐剂,选择全面调查 C、为了了解“天问一号”的设备零件的质量情况,选择抽样调查 D、为了了解某年福州市的空气质量,选择抽样调查5. 下列方程中,是二元一次方程的是( )A、3x-2=5 B、6x2-2=0 C、+y=3 D、5x+y=26. 不等式x<3的解集在数轴上表示为( )A、
A、 B、 C、 D、4. 下列调查中,调查方式选择合理的是( )A、为了了解某一批灯泡的寿命,选择全面调查 B、为了了解一批袋装食品是否含有防腐剂,选择全面调查 C、为了了解“天问一号”的设备零件的质量情况,选择抽样调查 D、为了了解某年福州市的空气质量,选择抽样调查5. 下列方程中,是二元一次方程的是( )A、3x-2=5 B、6x2-2=0 C、+y=3 D、5x+y=26. 不等式x<3的解集在数轴上表示为( )A、 B、
B、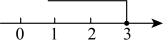 C、
C、 D、
D、 7. 方程组的解是( )A、 B、 C、 D、8. 已知 , 则下列各式中一定成立的是( )A、 B、 C、 D、9. 下列选项中,过点P画的垂线 , 三角板放法正确的是( )A、
7. 方程组的解是( )A、 B、 C、 D、8. 已知 , 则下列各式中一定成立的是( )A、 B、 C、 D、9. 下列选项中,过点P画的垂线 , 三角板放法正确的是( )A、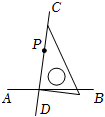 B、
B、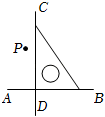 C、
C、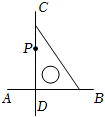 D、
D、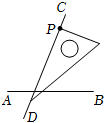 10. 阅读理解:我们把称作二阶行列式,规定它的运算法则为=ad-bc,例如=1×4-2×3=-2,如果>0,则x的取值范围是( )A、x>1 B、x<-1 C、x>3 D、x<-3
10. 阅读理解:我们把称作二阶行列式,规定它的运算法则为=ad-bc,例如=1×4-2×3=-2,如果>0,则x的取值范围是( )A、x>1 B、x<-1 C、x>3 D、x<-3二、填空题
-
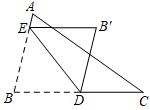
11. 的平方根是 .12. 已知 , 用含x的代数式表示y,则 .13. 如果点P(x,y)的坐标满足x+y=xy,那么称点P为“美丽点”,若某个“美丽点”P到y轴的距离为2,则点P的坐标为 .14. 若关于x、y的二元一次方程组 的解也是二元一次方程 的解,则k的值为.15. 如图所示,将三角形纸片ABC沿DE折叠,使点B落在点B′处,若EB′恰好与BC平行,且∠B=80°,则∠CDE=°.
三、解答题
-
16. 计算: .17. 解不等式组:并在数轴表示它的解集.
 18. 某校为了增强学生的安全意识,组织全校学生参加安全知识竞赛,赛后组委会随机抽查部分学生的成绩进行统计(由高到低分四个等级).根据调查的数据绘制成如下的条形统计图和扇形统计图.根据以上不完整的统计图提供的信息,解答下列问题:
18. 某校为了增强学生的安全意识,组织全校学生参加安全知识竞赛,赛后组委会随机抽查部分学生的成绩进行统计(由高到低分四个等级).根据调查的数据绘制成如下的条形统计图和扇形统计图.根据以上不完整的统计图提供的信息,解答下列问题: (1)、组委会共抽查了名学生的安全知识竞赛成绩,扇形统计图中级所占的百分比 , 扇形统计图中级所对应的圆心角的度数是度;(2)、补全条形统计图;(3)、若该校共有800名学生,请估算该校安全知识竞赛成绩获得级的人数.19. 如图所示,在边长为个单位的方格中,的三个顶点的坐标分别是 , , , 先将向上平移个单位长度,再向右平移个单位长度,得到
(1)、组委会共抽查了名学生的安全知识竞赛成绩,扇形统计图中级所占的百分比 , 扇形统计图中级所对应的圆心角的度数是度;(2)、补全条形统计图;(3)、若该校共有800名学生,请估算该校安全知识竞赛成绩获得级的人数.19. 如图所示,在边长为个单位的方格中,的三个顶点的坐标分别是 , , , 先将向上平移个单位长度,再向右平移个单位长度,得到 (1)、在图中画出;(2)、点 , , 的坐标分别为、、;(3)、若轴有一点 , 满足是面积的倍,请直接写出点的坐标.20. 请补全下面的证明.
(1)、在图中画出;(2)、点 , , 的坐标分别为、、;(3)、若轴有一点 , 满足是面积的倍,请直接写出点的坐标.20. 请补全下面的证明.如图,点E为DF的中点,点B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.

证明:∵(已知).
( ).
∴(等量代换),
∴ ▲ ▲ (内错角相等,两直角平行),
∴(两直线平行,同位角相等).
∵(已知),
∴ ▲ = ▲ (等量代换),
∴( ).
21. 某学校在疫情期间的复学准备工作中,为了贯彻落实“生命重于泰山,安全至关重要”的思想,计划购买室内、室外两种型号的消毒液.已知每桶室外消毒液的价格比每桶室内消毒液的价格多30元,买2桶室内消毒液和3桶室外消毒液共需340元.(1)、求室内、室外两种型号消毒液每桶的价格;(2)、根据学校实际情况,需购买室内、室外两种型号的消毒液共200桶,总费用不高于1.4万元,问室内消毒液至少要购买多少桶?22. 如图1,AM∥NC,点B位于AM,CN之间,∠BAM为钝角,AB⊥BC,垂足为点B.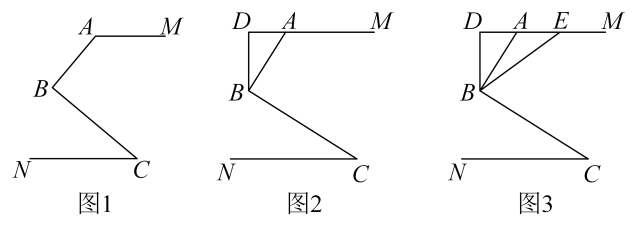 (1)、若∠C=40°,则∠BAM=;(2)、如图2,过点B作BD⊥AM,交MA的延长线于点D,求证:∠ABD=∠C;(3)、如图3,在(2)问的条件下,BE平分∠DBC交AM于点E,若∠C=∠DEB,求∠DEB的度数.23. 如图,以直角的直角顶点O为原点,以所在直线为x轴和y轴建立平面直角坐标系,点满足 ,
(1)、若∠C=40°,则∠BAM=;(2)、如图2,过点B作BD⊥AM,交MA的延长线于点D,求证:∠ABD=∠C;(3)、如图3,在(2)问的条件下,BE平分∠DBC交AM于点E,若∠C=∠DEB,求∠DEB的度数.23. 如图,以直角的直角顶点O为原点,以所在直线为x轴和y轴建立平面直角坐标系,点满足 , (1)、点A的坐标为;点C的坐标为 .(2)、已知坐标轴上有两动点同时出发,P点从C点出发沿x轴负方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度匀速移动,点P到达O点整个运动随之结束.的中点D的坐标是 , 设运动时间为t秒.问:是否存在这样的t,使得与的面积相等?若存在,请求出t的值;若不存在,请说明理由.(3)、在(2)的条件下,若点G是第二象限中一点,并且y轴平分 . 点E是线段上一动点,连接交于点H,当点E在线段上运动的过程中,探究之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).
(1)、点A的坐标为;点C的坐标为 .(2)、已知坐标轴上有两动点同时出发,P点从C点出发沿x轴负方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度匀速移动,点P到达O点整个运动随之结束.的中点D的坐标是 , 设运动时间为t秒.问:是否存在这样的t,使得与的面积相等?若存在,请求出t的值;若不存在,请说明理由.(3)、在(2)的条件下,若点G是第二象限中一点,并且y轴平分 . 点E是线段上一动点,连接交于点H,当点E在线段上运动的过程中,探究之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).