广东省梅州市大埔县2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 使分式 $\frac{7}{x - 2}$ 有意义的 $x$ 的取值范围是（）

A、 $x > 2$ B、 $x \neq 2$ C、 $x = 2$ D、 $x < 2$

查看试题解析
3. 多项式2x²﹣2y²分解因式的结果是（）

A、2（x+y）² B、2（x﹣y）² C、2（x+y）（x﹣y） D、2（y+x）（y﹣x）

查看试题解析
4. 不等式2x+1＞x+2的解集是（）

A、x＞1 B、x＜1 C、x≥1 D、x≤1

查看试题解析
5. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（）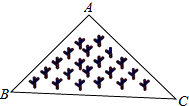

A、△ABC的三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三边的中垂线的交点

查看试题解析
6. 当 $a = 2023 - b$ 时，计算 $(a - \frac{b^{2}}{a}) \div \frac{a - b}{a}$ 的值为（）

A、2023 B、 $- 2023$ C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
7. 如果把分式 $\frac{3 y}{x + y}$ 中的x和y都扩大为原来的2倍，那么分式的值（）

A、扩大为原来的2倍 B、缩小为原来的 $\frac{1}{2}$ C、扩大为原来的6倍 D、不变

查看试题解析
8. 如图函数y=2x和y=ax+4的图象相交于A(m，3)，则不等式2x<ax+4的解集为（）

A、 $x < \frac{3}{2}$ B、 $x < 3$ C、 $x > \frac{3}{2}$ D、 $x > 3$

查看试题解析
9. 如图，AB∥CE ， ∠A＝40°，CE=DE ，则∠C的度数是（）

A、40° B、30° C、20° D、15°

查看试题解析
10. 如图，在平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则AB的长为（）

A、4 B、3 C、 $\frac{5}{2}$ D、2

查看试题解析

二、填空题

11. 用提取公因式法将多项式 $8 a^{3} b^{2} + 12 a^{3} b c - 4 a^{2} b$ 分解因式时，应提取的公因式是．

查看试题解析
12. 不等式 $2 x - 3 \leq 5 x$ 的非正整数解有个．

查看试题解析
13. 当 $x =$ 时，代数式 $\frac{1}{x - 1} + \frac{3}{1 - x^{2}}$ 的值为零．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $B D$ 是 $△ A B C$ 的角平分线，过点D作 $B C$ 的平行线，交 $A B$ 于点E，已知， $A E = 5$ ， $D E = 4$ ，则 $C D$ 的长为．

查看试题解析
15. 如下图，三角形纸片ABC，点D是BC边上一点，连接AD，把 $△ A B D$ 沿着AD翻折，得到 $△ A E D$ ， DE与AC交于点F．若点F是DE的中点， $A D = 8$ ， $△ A E F$ 的面积为9，则点B、E之间的距离为．

查看试题解析

三、解答题

16. 分解因式：

(1)、 $m^{3} - 16 m$

(2)、 $- 4 a^{2} x + 12 a x - 9 x$

查看试题解析
17. 解分式方程： $\frac{x - 2}{x - 3} = 2 - \frac{1}{3 - x}$ .

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 x - 5 < 0 \\ x - 2 (x + 1) < 0 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
19. 先化简，再求值： $\frac{x^{2} + 2 x + 1}{x^{2} - 1} \div (\frac{x}{x - 1} - 1)$ ，其中 $x = 2$ ．

查看试题解析
20. 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点分别是A（5，2），B（5，5），C（1，1）．

⑴画出△ABC向左平移5个单位得到的△A₁B₁C₁ ，点A，B，C的对应点分别为点A₁ ， B₁ ， C₁；

⑵画出△A₁B₁C₁绕点C₁顺时针旋转90°后得到的△A₂B₂C₁ ，点A₁ ， B₁的对应点分别为点A₂ ， B₂；

⑶请直接写出四边形A₂B₂B₁C₁的面积．

查看试题解析
21. 端午节是中国首个入选世界非遗的节日，日期是每年农历五月初五．民间有“赛龙舟”、“吃粽子”等习俗．某商场在端午节来临之际准备购进A、B两种粽子进行销售，据了解，用3000元购买A种粽子的数量（个）比用3360元购买B种粽子的数量（个）多40个，且B种粽子的单价（元/个）是A种粽子单价（元/个）的1.2倍．

(1)、求A、B两种粽子的单价各是多少？

(2)、若商场计划购进这两种粽子共2200个销售，且购买A种粽子的费用不多于购买B种粽子的费用，写出总费用y（元）与购买A种粽子的数量m（个）之间的关系式，并求出如何购买才能使总费用最低？最低是多少元？

查看试题解析
22. 如图，在△ABC中，AB＝AC ， AE是∠BAC的角平分线，点O为AB的中点，延长EO交△ABC的外角平分线于点F ．

(1)、求证：EO＝ $\frac{1}{2}$ AB；

(2)、试判断四边形ACEF的形状，并证明你的结论．

查看试题解析
23. 如图，在▱ABCD中，对角线AC，BD相交于点O，AB⊥AC，AB＝3cm，BC＝5cm.点P从A点出发沿AD方向匀速运动，速度为1cm/s.连接PO并延长交BC于点Q，设运动时间为t（0＜t＜5）.

(1)、当t为何值时，四边形ABQP是平行四边形？

(2)、设四边形OQCD的面积为y（cm²），求y与t之间的函数关系式；

(3)、是否存在某一时刻t，使点O在线段AP的垂直平分线上？若存在，求出t的值；若不存在，请说明理由.

查看试题解析