浙江省金华市金东区2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-15 类型:期末考试
一、单选题
-
1. 如图,“宸宸”、“琮琮”、“莲莲”是第十九届亚运会的吉祥物,通过下图平移能得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 神舟十六号前往中国空间站后,组合体的在轨质量将超过吨(千克),堪称中国载人航天的历史性时刻,数据用科学记数法表示为( )A、 B、 C、 D、3. 为调查某校学生对“2023年全国两会”的了解程度,某课外活动小组进行了抽样调查,下列样本中最具有代表性的是( )A、调查该校九年级的学生对“2023年全国两会”的了解程度 B、调查该校女生对“2023年全国两会”的了解程度 C、调查该校在篮球场打篮球的学生对“2023年全国两会”的了解程度 D、调查该校每班学号尾号为5的学生对“2023年全国两会”的了解程度4. 下列运算正确的是( )A、 B、 C、 D、5. 数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
2. 神舟十六号前往中国空间站后,组合体的在轨质量将超过吨(千克),堪称中国载人航天的历史性时刻,数据用科学记数法表示为( )A、 B、 C、 D、3. 为调查某校学生对“2023年全国两会”的了解程度,某课外活动小组进行了抽样调查,下列样本中最具有代表性的是( )A、调查该校九年级的学生对“2023年全国两会”的了解程度 B、调查该校女生对“2023年全国两会”的了解程度 C、调查该校在篮球场打篮球的学生对“2023年全国两会”的了解程度 D、调查该校每班学号尾号为5的学生对“2023年全国两会”的了解程度4. 下列运算正确的是( )A、 B、 C、 D、5. 数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( ) A、同旁内角、同位角、内错角 B、同位角、内错角、对顶角 C、对顶角、同位角、同旁内角 D、同位角、内错角、同旁内角6. 下列各式从左到右的变形,一定正确的是( )A、 B、 C、 D、7. 下列式子不能用平方差公式计算的是( )A、 B、 C、 D、8. 如果展开后的结果不含x的一次项,则k的值是( )A、0 B、 C、 D、69. 为了准备期末检测评价,小军去文具店购买了数支单价为2元的笔芯和若干块单价为k元的橡皮(k为正整数),共花费了6元,已知购买笔芯数量是橡皮数量的2倍,则小军购买的笔芯的数量为( )A、1支 B、2支 C、3支 D、4支10. 如图,直线 , 将一块含30°角的直角三角板ABC按如图所示放置(),边交直线于点 , 边交直线于点 , 边分别交直线于点 , 在线段上取一点 , 连结 , 且有 , 则的值为( )
A、同旁内角、同位角、内错角 B、同位角、内错角、对顶角 C、对顶角、同位角、同旁内角 D、同位角、内错角、同旁内角6. 下列各式从左到右的变形,一定正确的是( )A、 B、 C、 D、7. 下列式子不能用平方差公式计算的是( )A、 B、 C、 D、8. 如果展开后的结果不含x的一次项,则k的值是( )A、0 B、 C、 D、69. 为了准备期末检测评价,小军去文具店购买了数支单价为2元的笔芯和若干块单价为k元的橡皮(k为正整数),共花费了6元,已知购买笔芯数量是橡皮数量的2倍,则小军购买的笔芯的数量为( )A、1支 B、2支 C、3支 D、4支10. 如图,直线 , 将一块含30°角的直角三角板ABC按如图所示放置(),边交直线于点 , 边交直线于点 , 边分别交直线于点 , 在线段上取一点 , 连结 , 且有 , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
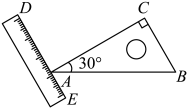
11. 要使分式有意义,x的取值应满足 .12. 如图,是一块直角三角板,其中 , 直尺的一边经过顶点A,若 , 则的度数为 .
 13. 若是关于的整式的完全平方,则实数的值为 .14. 已知关于x,y的方程组 , 下列结论:①当x,y互为相反数时,;②无论a取何值,这个方程组的解也是方程的解;③无论a取何值,的值不变;④;其中正确的有(填写序号).15. 若 , 则 .16. 我国南宋数学家杨辉在《续古摘奇算法》中的攒九图中提出“幻圆”的概念.如图是一个简单的二阶幻圆模型,若内外两个圆周上四个数字之和以及外圆两直径上的四个数字之和都相等,则; .
13. 若是关于的整式的完全平方,则实数的值为 .14. 已知关于x,y的方程组 , 下列结论:①当x,y互为相反数时,;②无论a取何值,这个方程组的解也是方程的解;③无论a取何值,的值不变;④;其中正确的有(填写序号).15. 若 , 则 .16. 我国南宋数学家杨辉在《续古摘奇算法》中的攒九图中提出“幻圆”的概念.如图是一个简单的二阶幻圆模型,若内外两个圆周上四个数字之和以及外圆两直径上的四个数字之和都相等,则; .
三、解答题
-
17. 计算:(1)、(2)、18. 如图是正在进行的俄罗斯方块游戏(网格由边长为个单位长度的小正方形组成),现出现一“T”形方块向下运动.
 (1)、若该“T”形方块向下平移了个单位长度,请在图中画出平移后的图形(并画上阴影).(2)、为了使所有图案消除,在(1)的平移基础上还需进行怎样的平移?(俄罗斯方块游戏规则:①当方块排列成完整的一行,该行便可消除;②方块在下落过程中,若碰到下方已有的方块便不可移动 . )19. 解方程(组):(1)、(2)、20. 如图,直线分别交直线于点E,点F, , 平分交于点G.
(1)、若该“T”形方块向下平移了个单位长度,请在图中画出平移后的图形(并画上阴影).(2)、为了使所有图案消除,在(1)的平移基础上还需进行怎样的平移?(俄罗斯方块游戏规则:①当方块排列成完整的一行,该行便可消除;②方块在下落过程中,若碰到下方已有的方块便不可移动 . )19. 解方程(组):(1)、(2)、20. 如图,直线分别交直线于点E,点F, , 平分交于点G.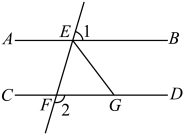 (1)、求证: .(2)、若 , 求的度数.21. 阅读以下内容,完成问题.
(1)、求证: .(2)、若 , 求的度数.21. 阅读以下内容,完成问题.解:
①
②
③
④
 (1)、小明的计算步骤中,从哪一步开始出现错误?(填写序号)(2)、小明从第①步的运算结果到第②步的运算是否正确?(填“是”或“否”)若不正确,错误的原因是 .(3)、请你帮小明写出此题完整正确的解答过程.22. 2023年金华市共有60000余名学生参加初中毕业生体育学业考试.为了了解我市毕业生的排球成绩,随机抽取了50名考生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A,B,C,D表示)四个等级进行统计,并绘制成下面的扇形图和统计表.请你根据以下图表提供的信息,解答下列问题:
(1)、小明的计算步骤中,从哪一步开始出现错误?(填写序号)(2)、小明从第①步的运算结果到第②步的运算是否正确?(填“是”或“否”)若不正确,错误的原因是 .(3)、请你帮小明写出此题完整正确的解答过程.22. 2023年金华市共有60000余名学生参加初中毕业生体育学业考试.为了了解我市毕业生的排球成绩,随机抽取了50名考生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A,B,C,D表示)四个等级进行统计,并绘制成下面的扇形图和统计表.请你根据以下图表提供的信息,解答下列问题:50名考生排球测试成绩统计表
等级
成绩(满分5分)
频数(人数)
频率
A
5分
19
B
4~5分(包括4分但不包括5分)
a
x
C
3~4分(包括3分但不包括4分)
b
y
D
3分以下(不包括3分)
3
合计
50
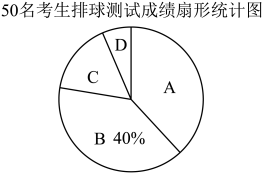 (1)、 , , , .(2)、在扇形图中,求C等级所对应的圆心角的度数.(3)、请你估计我市考生中,成绩等级达到优秀和良好的共有多少人(总人数按60000名计算)?23. 【发现问题】数形结合是解决数学问题的一种重要的思想方法,借助图的直观性,可以帮助我们更容易理解数学问题.现有图1中的A,B,C三种卡片若干,用这些卡片可以拼成各式各样的图形,根据这些图形的面积的不同表示可以将一些多项式因式分解.
(1)、 , , , .(2)、在扇形图中,求C等级所对应的圆心角的度数.(3)、请你估计我市考生中,成绩等级达到优秀和良好的共有多少人(总人数按60000名计算)?23. 【发现问题】数形结合是解决数学问题的一种重要的思想方法,借助图的直观性,可以帮助我们更容易理解数学问题.现有图1中的A,B,C三种卡片若干,用这些卡片可以拼成各式各样的图形,根据这些图形的面积的不同表示可以将一些多项式因式分解.
例:用1张A卡片,2张B卡片,1张C卡片拼成如图2的图形,用两种方法表示该图形的面积,可以得到等式 , 这种把一个多项式化成几个整式的积的形式,叫做因式分解.
(1)、【小试牛刀】请把表示图3面积的多项式因式分解(直接写出等式即可).
(2)、【自主探索】请利用图1的卡片,将多项式因式分解,并画出图形.
(3)、【拓展迁移】事实上,拼图不仅限于平面图形,利用立体图形的体积也可以将一些多项式因式分解.请你用此方法从体积角度简要说明如何把进行因式分解并写出因式分解结果.
24. 阅读以下微信群聊,完成任务.

任务一:该“旅行团”有几种打车方案?哪种方案比较划算?
任务二:小胡家的两间“亲子家庭房”共花费多少钱?
任务三:该“旅行团”分别购买了“380”和“580”这两种票价的门票各多少张?

