浙江省杭州市上城区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-15 类型:期末考试
一、单选题
-
1. 下列与杭州亚运会有关的图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式,计算正确的是( )A、 B、 C、 D、3. 菱形具有而矩形不具有的性质是 .A、对角线互相平分 B、对角相等 C、对角线互相垂直 D、对边平行且相等4. 若用反证法证明命题“在中,若 , 则”,则应假设( )A、 B、 C、 D、5. 若关于x的一元二次方程的一个实数根为2,则另一实数根和m的值分别为( )A、 , B、 , 8 C、4, D、4,86. 在学校举办的“数学思维挑战赛”中,有19名选手进入决赛,前9名将晋级更高一级比赛,他们的决赛成绩各不相同,其中一名选手想知道自己是否晋级,除了知道自己的成绩外,他还需要了解这19名学生成绩的( )A、平均数 B、中位数 C、众数 D、方差7. 如图,点E、F分别是边的中点,点D是上一点,且 . 若 , 则的长为( )
2. 下列各式,计算正确的是( )A、 B、 C、 D、3. 菱形具有而矩形不具有的性质是 .A、对角线互相平分 B、对角相等 C、对角线互相垂直 D、对边平行且相等4. 若用反证法证明命题“在中,若 , 则”,则应假设( )A、 B、 C、 D、5. 若关于x的一元二次方程的一个实数根为2,则另一实数根和m的值分别为( )A、 , B、 , 8 C、4, D、4,86. 在学校举办的“数学思维挑战赛”中,有19名选手进入决赛,前9名将晋级更高一级比赛,他们的决赛成绩各不相同,其中一名选手想知道自己是否晋级,除了知道自己的成绩外,他还需要了解这19名学生成绩的( )A、平均数 B、中位数 C、众数 D、方差7. 如图,点E、F分别是边的中点,点D是上一点,且 . 若 , 则的长为( ) A、1 B、2 C、3 D、48. 若点都在反比例函数的图象上,下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 已知关于的方程(为常数,且),下列的值,哪个一定不是方程的解( )A、 B、 C、 D、10. 如图,将菱形沿折叠,点B的对应点为F,若E、F、D刚好在同一直线上,设 , , , 则关系正确的是( )
A、1 B、2 C、3 D、48. 若点都在反比例函数的图象上,下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 已知关于的方程(为常数,且),下列的值,哪个一定不是方程的解( )A、 B、 C、 D、10. 如图,将菱形沿折叠,点B的对应点为F,若E、F、D刚好在同一直线上,设 , , , 则关系正确的是( )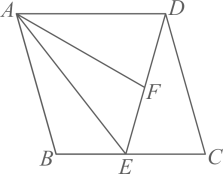 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若代数式 有意义,则实数x 的取值范围是.12. 如果一个n边形的内角和等于它的外角和,则n= .13. 在50米跑的10次训练中,小明的成绩的平均数为8.2秒,方差为2.2,第11次小明的成绩为8.2秒,则小明这11次的50米跑成绩与前10次的成绩相比较,其平均数 , (填“变大”、“变小”或“不变”),方差 . (填“变大”、“变小”或“不变”)14. 一高尔夫球手某次击出一个高尔夫球的高度h(米)和经过的水平距离d(米)可用公式来估计.当球的高度第二次达到16米时,球的水平距离是米.15. 如图,两个全等的矩形纸片重叠在一起,矩形的长和宽分别是4和3,则重叠部分的四边形ABCD面积是 .
 16. 有学者认为,阿拉伯数学家花拉子米的《代数学》关于一元二次方程的几何求解法与中国古代数学的“出入相补原理”相近,可能受到中国传统数学思想的影响,花拉子米关于的几何求解方法如图1,在边长为x的正方形的四个边上向外做边长为x和的矩形,再把它补充成一个边长为的大正方形,我们得到大正方形的面积为(因为).所以大正方形边长为 , 得到 . 思考:当我们用这种方法寻找的解时,如图2中间小正方形的边长x为;阴影部分每个正方形的边长为 .
16. 有学者认为,阿拉伯数学家花拉子米的《代数学》关于一元二次方程的几何求解法与中国古代数学的“出入相补原理”相近,可能受到中国传统数学思想的影响,花拉子米关于的几何求解方法如图1,在边长为x的正方形的四个边上向外做边长为x和的矩形,再把它补充成一个边长为的大正方形,我们得到大正方形的面积为(因为).所以大正方形边长为 , 得到 . 思考:当我们用这种方法寻找的解时,如图2中间小正方形的边长x为;阴影部分每个正方形的边长为 .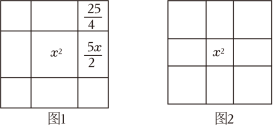
三、解答题
-
17. 计算:(1)、;(2)、 .18. 解方程:(1)、;(2)、 .19. 如图,在中,点在的延长线上,且 . 求证: .
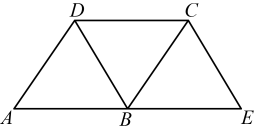 20. 为迎接杭州亚运会,学校举办“亚运会知识竞赛”,初赛共道题,每题分,小乘从初赛名单中随机抽取部分同学的成绩,绘制出如下的统计图和图 . 请根据相关信息,解答下列问题:
20. 为迎接杭州亚运会,学校举办“亚运会知识竞赛”,初赛共道题,每题分,小乘从初赛名单中随机抽取部分同学的成绩,绘制出如下的统计图和图 . 请根据相关信息,解答下列问题: (1)、图中的值为 ▲ , 补全条形统计图;(2)、求被抽取的初赛成绩的平均数,众数和中位数;(3)、如果初赛成绩在分或分以上的同学进入复赛,请估计参加初赛的位同学中有多少同学可以参加复赛.21. 已知反比例函数 , 点都在该反比例函数图象上.
(1)、图中的值为 ▲ , 补全条形统计图;(2)、求被抽取的初赛成绩的平均数,众数和中位数;(3)、如果初赛成绩在分或分以上的同学进入复赛,请估计参加初赛的位同学中有多少同学可以参加复赛.21. 已知反比例函数 , 点都在该反比例函数图象上. (1)、求反比例函数的表达式;(2)、当时,直接写出y的取值范围;(3)、若经过的直线与y轴交于点C,求的面积.22. 在中,E,F为上的两点,且 , .
(1)、求反比例函数的表达式;(2)、当时,直接写出y的取值范围;(3)、若经过的直线与y轴交于点C,求的面积.22. 在中,E,F为上的两点,且 , . (1)、求证:;(2)、求证:是矩形;(3)、连接 , 若是的平分线, , , 求四边形的面积.23. 综合实践:
(1)、求证:;(2)、求证:是矩形;(3)、连接 , 若是的平分线, , , 求四边形的面积.23. 综合实践:项目主题
“亚运主题”草坪设计
项目情境
为了迎亚会,同学们参与一块长为40米,宽为30米的矩形“亚运主题”草
坪方案设计的项目学习.以下为项目学习小组对草坪设计的研究过程.
活动任务一
请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案

驱动问题一
(1)项目小组设计出来的四种方案小路面积的大小关糸?
①直观猜想:我认为 ▲ ;(请用简洁的语言或代数式表达你的猜想)
②具体验证:选择最简单的甲、乙方案,假设小路宽为1米,则甲、乙方案中小路的面积分别为 ▲ 和 ▲ ;
③一般验证:若小路宽为x米,则甲、乙方案中小路所占的面积分别为 ▲ 和 ▲ .
活动任务二
为施工方便,学校选择甲种方案设计,并要求除小路后草坪面积约为1064平方米.
驱动问题二
(2)请计算两条小路的宽度是多少?
活动任务三
为了布置五环标志等亚运元素,将在草坪上的亚运宣传主题墙前,用篱笆围(三边)成面积为100平方米的矩形 , 如图.
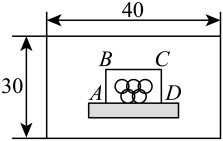
驱动问题三
(3)为了使篱笆恰好用完同时围住三面,项目小组的同学对下列问题展开探究,其中矩形宽 , 长 .
①若30米长的篱笆,请用两种不同的函数表示y关于x的函数关系.
②数学之星小明提出一个问题:若a米长的篱笆恰好用完,且有两种不同方案可以选择,使得两种方案的宽之和小于15米,甲同学说“篱笆的长可以是28米”,乙同学说“篱笆的长可以是32米”,你认为他们俩的说法对吗?请说明理由.