广东省广州市白云区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-15 类型:期末考试
一、单选题
-
1. 一次函数y=x+2的图象与y轴的交点坐标为( )A、(0,2) B、(0,-2) C、(2,0) D、(-2,0)2. 若二次根式有意义,则的取值范围是( )A、 B、 C、 D、3. 一组数据:5,7,6,3,4的平均数是( )A、5 B、6 C、4 D、84. 一次函数 , 且函数值y随自变量x的增大而减小,则k有可能是( )A、0 B、3 C、 D、5. 在▱ABCD中(如图),连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=( )
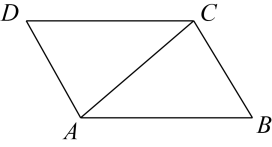 A、80° B、100° C、120° D、140°6. 以下列各组数为边长,能构成直角三角形的是( )A、 , , 2 B、1,2, C、1, , D、4,5,67. 已知且 , 则一次函数的图象大致是( )A、
A、80° B、100° C、120° D、140°6. 以下列各组数为边长,能构成直角三角形的是( )A、 , , 2 B、1,2, C、1, , D、4,5,67. 已知且 , 则一次函数的图象大致是( )A、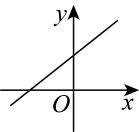 B、
B、 C、
C、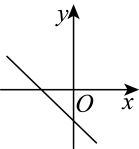 D、
D、 8. 如图,已知平行四边形ABCD的对角线AC与BD相交于点O,下列结论中,不正确的是( )
8. 如图,已知平行四边形ABCD的对角线AC与BD相交于点O,下列结论中,不正确的是( ) A、当AB⊥AD时,四边形ABCD是矩形 B、当AC⊥BD时,四边形ABCD是菱形 C、当OA=OB时,四边形ABCD是矩形 D、当AB=AC时,四边形ABCD是菱形9. 如图,在直线l上有正方形a,b,c,若a,c的面积分别为4和16,则b的面积为( )
A、当AB⊥AD时,四边形ABCD是矩形 B、当AC⊥BD时,四边形ABCD是菱形 C、当OA=OB时,四边形ABCD是矩形 D、当AB=AC时,四边形ABCD是菱形9. 如图,在直线l上有正方形a,b,c,若a,c的面积分别为4和16,则b的面积为( ) A、24 B、20 C、12 D、2210. 如图,点A的坐标为 , 点B在直线上运动,当线段最短时,点B的坐标为( )
A、24 B、20 C、12 D、2210. 如图,点A的坐标为 , 点B在直线上运动,当线段最短时,点B的坐标为( ) A、(0,0) B、 C、 D、
A、(0,0) B、 C、 D、二、填空题
-
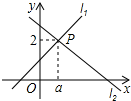
11. 计算: × = .12. 把直线向上平移2个单位长度,则平移后所得直线的解析式为 .13. 菱形的一条对角线长为 ,面积是 ,则菱形的另一条对角线长为cm.14. 命题“对顶角相等”的逆命题是15. 直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
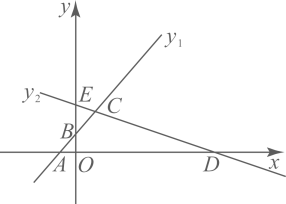
 16. 如图,在直角坐标系中,点A的坐标为 , 以线段为边在第四象限内作等边 , 点为x轴正半轴上一动点,连接 , 以线段为边在第四象限内作等边 , 直线交y轴于点E , 则四边形的面积是 . (结果用含a的式子表示)
16. 如图,在直角坐标系中,点A的坐标为 , 以线段为边在第四象限内作等边 , 点为x轴正半轴上一动点,连接 , 以线段为边在第四象限内作等边 , 直线交y轴于点E , 则四边形的面积是 . (结果用含a的式子表示)
三、解答题
-
17. 化简: .18. 计算: .19. 已知一次函数的图象经过 , 两点.(1)、求此一次函数表达式;(2)、试判断点是否在此一次函数的图象上.20. 如图,在平行四边形中,E,F分别是 , 的中点,求证: .
 21. 某校为了改善学生伙食,准备午餐为学生提供鸡翅,现有A , B两家副食品厂可以提供规格为75g的鸡翅,而且它们的价格相同,品质也相近,质检人员分别从两家随机各抽取10个,记录它们的质量(单位:g)如下:
21. 某校为了改善学生伙食,准备午餐为学生提供鸡翅,现有A , B两家副食品厂可以提供规格为75g的鸡翅,而且它们的价格相同,品质也相近,质检人员分别从两家随机各抽取10个,记录它们的质量(单位:g)如下:A副食品厂:74,74,74,75,73,77,78,72,76,77.
B副食品厂:78,74,77,73,75,75,74,74,75,75.
并对以上数据进行整理如下:
平均数
中位数
众数
方差
A副食品厂
75
74.5
b
3.4
B副食品厂
75
a
75
2
根据以上分析,回答下列问题:
(1)、统计表中 , ;(2)、根据以上信息估计B副食品厂加工的100个鸡翅中,质量为75g的鸡翅有多少个?(3)、如果只考虑鸡翅质量与规格的匹配程度,学校应该选购哪家副食品厂的鸡翅?说明理由.22. 如图,已知 , , , . (1)、尺规作图,作边上的高;(不必写作法,保留作图痕迹)(2)、求的面积.23. 观察下列各式,回答问题:
(1)、尺规作图,作边上的高;(不必写作法,保留作图痕迹)(2)、求的面积.23. 观察下列各式,回答问题:①;②;③ .
(1)、上述式子中,正确的是;(2)、类比上述式子,可得第④个式子是;(3)、从(1),(2)的结论中,你能看出其中的规律吗?用字母表示这一规律,并给出证明.