2023年浙教版数学九年级上册2.3 用频率估计概率同步测试（提高版）

试卷更新日期：2023-08-13 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 某射击运动员在同一条件下的射击成绩记录如下：
射击次数
20
80
100
200
400
1000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性，估计这名运动员射击一次时“射中九环以上”的概率约是（）

A、0.90 B、0.85 C、0.82 D、0.84

查看试题解析
2. 在一个不透明的布袋中装有30个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在 $0 ． 4$ 左右，则布袋中白球可能有（）

A、12个 B、15个 C、18个 D、20个

查看试题解析
3. 为了解某地区九年级男生的身高情况，随机抽取了该地区200名九年级男生，他们的身高 $x (c m)$ 统计如下：

组别 $(c m)$

$x < 160$

$160 \leq x < 170$

$170 \leq x < 180$

$x \geq 180$

人数

10

m

n

42

根据以上结果，抽查该地区一名九年级男生，估计他的身高不低于180cm的概率是（　　）

A、0.42 B、0.21 C、0.79 D、与m，n的取值有关

查看试题解析

4. 如表是一位同学在罚球线上投篮的试验结果，根据表中数据回答下列问题：

投篮次数 $(n)$	50	100	150	200	250	300	500
投中次数 $(m)$	28	60	78	104	124	153	252

估计这位同学投篮一次，投中的概率约是（精确到0.1）（）

A、0.4 B、0.5 C、0.55 D、0.6

查看试题解析

5. 某人在做抛掷硬币试验中，抛掷n次，正面朝上有m次，若正面朝上的频率是P＝ $\frac{m}{n}$ ，则下列说法正确的是（）

A、P一定等于0.5 B、多投一次，P更接近0.5 C、P一定不等于0.5 D、投掷次数逐渐增加，P稳定在0.5附近

查看试题解析
6. 在一个暗箱里放有 $m$ 个除颜色外完全相同的球，这 $m$ 个球中红球只有4个，每次将球充分摇匀后，随机从中摸出一球，记下颜色后放回，通过大量的重复试验后发现，摸到红球的频率为0.4，由此可以推算出 $m$ 约为（）

A、7 B、3 C、10 D、6

查看试题解析
7. 利用六张编号为1，2，3，4，5，6的扑克牌进行频率估计概率的试验中，同学小张统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的试验可能是（）

A、抽中的扑克牌编号是3的概率 B、抽中的扑克牌编号是3的倍数的概率 C、抽中的扑克牌编号大于3的概率 D、抽中的扑克牌编号是偶数的概率

查看试题解析
8. 某水果超市为了吸引顾客来店购物，设立了一个如图所示的可以自由转动的转盘，开展有奖购物活动.顾客购买商品满200元就能获得一次转动转盘的机会，当转盘停止时，指针落在“一袋苹果”的区域就可以获得一袋苹果；指针落在“一袋橘子”的区域就可以获得一袋橘子.若转动转盘2000次，指针落在“一袋橘子”区域的次数有600次，则某位顾客转动转盘一次，获得一袋橘子的概率大约是（）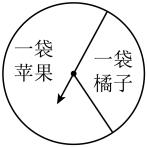

A、0.3 B、0.7 C、0.4 D、0.2

查看试题解析
9. 随机抽检一批毛衫的合格情况，得到如下的频数表.下列说法错误的是（）
抽取件数（件）
100
150
200
500
800
1000
合格频数
a
141
190
475
764
950
合格频率
0.90
0.94
b
0.95
0.955
0.95

A、抽取100件的合格频数是90 B、抽取200件的合格频率是0.95 C、任抽一件毛衫是合格品的概率为0.90 D、出售2000件毛衫，次品大约有100件

查看试题解析
10. 一个袋子中装有12个球（袋中每个球除颜色外其余都相同）．某活动小组想估计袋子中红球的个数，分10个组进行摸球试验，每一组做400次试验，汇总后，摸到红球的次数为 3000次．请你估计袋中红球接近（）

A、3 B、4 C、6 D、9

查看试题解析

二、填空题（每空4分，共24分）

11. 某射击运动员封闭训练10个月，每天击中9环以上的频率记录如下图，封闭训练结束时，估计这名运动员射击一次时“击中9环以上”的概率为（结果保留一位小数）．

查看试题解析
12. 小文将学校二维码打印在面积为400cm²的正方形纸上，如图所示，为了估计图中黑色部分的面积，她在纸内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，据此可以估计黑色部分的面积约为 cm² ．

查看试题解析
13. 淘宝某商户为了解新商品主图是否吸引人，对该商品的点击量和展现量进行了监测，得到商品点击率如下表所示：（注： $点击率 = \frac{点击量}{展现量} \times 100 %$ ）
展现量
50
100
1000
5000
10000
50000
100000
点击量
4
7
78
385
760
3800
7600
点击率
$8.0 %$
$7.0 %$
$7.8 %$
$7.7 %$
$7.6 %$
$7.6 %$
$7.6 %$
根据上表，估计该商品展现量为30000时，点击率约为.

查看试题解析
14. 做任意抛掷一只纸杯的重复试验，获得如下表数据：
抛掷总次数
100
200
300
400
杯口朝上频数
20
42
66
88
杯口朝上频率
0.2
0.21
0.22
0.22
则估计任意抛掷一只纸杯杯口朝上的概率约为（结果精确到0.01）.

查看试题解析
15. 一个不透明的口袋中装有红色、黄色、蓝色玻璃球共200个，这些球除颜色外都相同.小明通过大量随机摸球试验后，发现摸到红球的频率稳定在 $30 %$ 左右，则可估计红球的个数约为.

查看试题解析
16. 在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同. 小明通过多次实验发现，摸出红球的频率稳定在0.3左右，则袋子中红球的大约有个.

查看试题解析

三、解答题（共9题，共66分）

17. 小颖和小红两位同学在学习“概率”时，做掷骰子（质地均匀的正方体）实验．

(1)、他们在一次实验中共掷骰子60次，试验的结果如下：

朝上的点数

1

2

3

4

5

6

出现的次数

7

9

6

8

20

10

①填空：此次实验中“5点朝上”的频率为 ▲ ；

②小红说：“根据实验，出现5点朝上的概率最大．”她的说法正确吗？为什么？

(2)、小颖和小红在实验中如果各掷一枚骰子，那么两枚骰子朝上的点数之和为多少时的概率最大？试用列表或画树状图的方法加以说明，并求出其最大概率．

查看试题解析

18. 在一个不透明的袋子里装有只有颜色不同的红、白两种颜色的球共5个．某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色．再把它放回袋中．不断重复，下表是活动中的一组统计数据：

摸球的次数n	100	150	300	500	800	1000
摸到白球的次数m	54	98	174	295	484	602
摸到白球的频率 $\frac{m}{n}$	0.54	0.65	0.58	0.59	0.603	0.602

(1)、请估计，当n很大时，摸到白球的概率接近（结果精确到0.1）．

(2)、试估算口袋中白球的个数．

(3)、在-次摸球游戏中，小明发现先后摸两次球（第一次放回），第一次摸到白球的概率为

\frac{3}{5}

，第二次摸到白球的概率也为

\frac{3}{5}

，那么两次都摸到白球的概率为

\frac{3}{5}

\frac{3}{5}

\frac{9}{25}

，根据以上信息，求事件A （第一次摸到红球，第二次摸到白球）的概率．

查看试题解析

19. 如图，地面上有一个不规则的封闭图形ABCD，为求得它的面积，小明设计了一个如下方法：

①在此封闭图形内画出一个半径为1米的圆．

②在此封闭图形旁边闭上眼睛向封闭图形内掷小石子（可把小石子近似地看成点），记录如下：

掷小石子落在不规则图形内的总次数	50	150	300	500	…
小石子落在圆内（含圆上）的次数m	20	59	123	203	…
小石子落在圆外的阴影部分（含外缘）的次数n	29	91	176	293	…
m：n	0.689	0.694	0.689	0.706

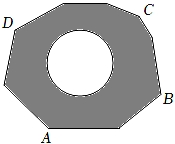(1)、通过以上信息，可以发现当投掷的次数很大时，则m：n的值越来越接近（结果精确到0.1）．

(2)、若以小石子所落的有效区域为总数（即m+n），则随着投掷次数的增大，小石子落在圆内（含圆上）的频率值稳定在附近（结果精确到0.1）．

(3)、请你利用（2）中所得频率的值，估计整个封闭图形ABCD的面积是多少平方米？（结果保留π）

查看试题解析

20. 一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：

摸球的次数	200	300	400	1000	1600	2000
摸到白球的频数	72	93	130	334	532	667
摸到白球的频率	0.3600	0.3100	0.3250	0.3340	0.3325	0.3335

(1)、该学习小组发现，摸到白球的频率在一个常数附近摆动，这个常数是（精确到0.01），由此估出红球有个.

(2)、现从该袋中按上述方式摸出2个球，请用树状图或列表的方法列出所有等可能的结果，并求恰好摸到1个白球，1个红球的概率.

查看试题解析

21. 在一个不透明的口袋里装有若干个相同的红球，为了估计袋中红球的数量，九（2）班学生在数学实验室分组做摸球实验：每组先将15个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表：
摸球的次数s
150
300
600
900
1200
1500
摸到红球的频数n
63
123
247
365
484
603
摸到红球的频率 $\frac{n}{s}$
0.420
0.410
0.412
0.406
0.403
a

(1)、a＝.

(2)、请估计：当次数s很大时，摸到红球的频率将会接近（精确到0.01）；请推测：摸到红球的概率是（精确到0.1）.

(3)、求口袋中红球的数量.

查看试题解析

22. 有一个圆形转盘，分黑色、白色两个区域.

(1)、某人转动转盘，对指针落在黑色区域或白色区域进行了大量试验，得到数据如下表：

实验次数n(次)	10	100	2000	5000	10000	50000	100000
白色区域次数m(次)	3	34	680	1600	3405	16500	33000
落在白色区域频率 $\frac{m}{n}$	0.3	0.34	0.34	0.32	0.34	0.33	0.33

请你利用上述实验，估计转动该转盘指针落在白色区域的概率为

(2)、若该圆形转盘白色扇形的圆心角为120度，黑色扇形的圆心角为240°，转动转盘两次，求指针一次落在白色区域，另一次落在黑色区域的概率.

查看试题解析

23. 一个黑箱子里装有红、白两种颜色的球4只，他们除颜色外，其他都相同，小明将球搅匀后从箱子中随机摸出一个球，记下颜色，再把它放回不断重复实验，将多次实验结果画出如下频率统计图.

(1)、当摸球次数很大时，摸到白球的频率将会接近（精确到0.01），从箱子中摸一次球，摸到红球的概率是；

(2)、从该箱子里随机摸出一个球，不放回，再摸出一个球.用树状图或列表法求出摸到一个红球一个白球的概率.

查看试题解析

24. 某地响应国家号召，将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其它垃圾四类，并分别设置了相应的垃圾箱.为调查该地居民生活垃圾的正确分类投放情况，现随机抽取了该地四类垃圾箱中总计1000吨生活垃圾，数据统计如下（单位：吨）：

	“厨余垃圾”箱	“可回收物”箱	“有害垃圾”箱	“其它垃圾”箱
厨余垃圾	400	100	40	60
可回收物	30	140	10	20
有害垃圾	5	20	60	15
其他垃圾	25	15	20	40

(1)、估算该地“有害垃圾”被正确投放在“有害垃圾箱”的概率.

(2)、已知该地一个月有5600吨生活垃圾，问投放错误的有害垃圾大约有几吨？

查看试题解析

25. 在3件同型号的产品 $A$ 、 $B$ 、 $C$ 中， $A$ 为不合格产品，其余2件为合格产品.

(1)、从这3件产品中随机抽取2件进行检测，请用树状图或列表法求出抽到的2件都是合格品的概率；

(2)、在这3件产品中加入 $x$ 件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的概率稳定在 $0.95$ ，则可以推算出 $x$ 的值大约是多少？

查看试题解析

射击次数	20	80	100	200	400	1000
“射中九环以上”的次数	18	68	82	168	327	823
“射中九环以上”的频率(结果保留两位小数)	0.90	0.85	0.82	0.84	0.82	0.82

组别 $(c m)$	$x < 160$	$160 \leq x < 170$	$170 \leq x < 180$	$x \geq 180$
人数	10	m	n	42

抽取件数（件）	100	150	200	500	800	1000
合格频数	a	141	190	475	764	950
合格频率	0.90	0.94	b	0.95	0.955	0.95

展现量	50	100	1000	5000	10000	50000	100000
点击量	4	7	78	385	760	3800	7600
点击率	$8.0 %$	$7.0 %$	$7.8 %$	$7.7 %$	$7.6 %$	$7.6 %$	$7.6 %$

抛掷总次数	100	200	300	400
杯口朝上频数	20	42	66	88
杯口朝上频率	0.2	0.21	0.22	0.22

摸球的次数s	150	300	600	900	1200	1500
摸到红球的频数n	63	123	247	365	484	603
摸到红球的频率 $\frac{n}{s}$	0.420	0.410	0.412	0.406	0.403	a

朝上的点数	1	2	3	4	5	6
出现的次数	7	9	6	8	20	10

2023年浙教版数学九年级上册2.3 用频率估计概率 同步测试（提高版）

一、选择题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共9题，共66分）

2023年浙教版数学九年级上册2.3 用频率估计概率同步测试（提高版）