2023年浙教版数学九年级上册2.2 简单事件的概率同步测试（培优版）

试卷更新日期：2023-08-13 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 在一个不透明的盒子中，装有质地、大小一样的白色乒乓球2个，黄色乒乓球3个，随机摸出一个球，摸到黄色乒乓球的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{3}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
2. 从下列命题中，随机抽取一个是真命题的概率是（）
⑴无理数都是无限小数；

⑵因式分解 $a x^{2} - a = a (x + 1) (x - 1)$ ；

⑶棱长是 $1 c m$ 的正方体的表面展开图的周长一定是 $14 c m$ ；

⑷两条对角线长分别为6和8的菱形的周长是40．

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
3. “宫商角徵羽”是中国古乐的五个基本音阶（相当于西乐的1，2，3，5，6），是采用“三分损益法”通过数学方法获得．现有一款“一起听古音”的音乐玩具，音乐小球从A处沿轨道进入小洞就可以发出相应的声音，且小球进入每个小洞的可能性大小相同．现有一个音乐小球从A处先后两次进入小洞，先发出“商”音，再发出“羽”音的概率是（）

A、 $\frac{1}{25}$ B、 $\frac{1}{10}$ C、 $\frac{1}{5}$ D、 $\frac{2}{5}$

查看试题解析
4. 下列说法正确的是（）

A、扇形统计图能够清楚地反映事物的变化趋势 B、对某型号电子产品的使用寿命采用全面调查的方式 C、有一种游戏的中奖概率是 $\frac{1}{5}$ ，则做5次这样的游戏一定会有一次中奖 D、甲、乙两组数据的平均数相等，它们的方差分别是 $S_{甲}^{2} = 0.2$ ， $S_{乙}^{2} = 0.03$ ，则乙比甲稳定

查看试题解析
5. 公园一张圆桌旁有 $4$ 个座椅，工作人员对座椅涂色，其中 $1$ 个座椅已涂上红色如图所示，要求其他的 $3$ 个座椅分别涂上黄、蓝、绿三种颜色（三种颜色都要有），则黄色与红色不相邻的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
6. 游仙是三国故地，古绵治所，历史悠久，风景优美．富乐山，越王楼，仙海风景区，绵阳科技馆已是游仙响亮的代名词．某校课外兴趣小组设计了4张旅游宣传卡片，正面图案如图所示，它们除此之外完全相同．将这4张卡片背面朝上，洗匀，从中随机抽取两张，则抽取的卡片正面图案恰好是“富乐山”和“越王楼”的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
7. 掷一枚质地均匀的硬币m次，正面向上n次，则 $\frac{n}{m}$ 的值（）

A、一定是 $\frac{1}{2}$ B、随着m的增大，在 $\frac{1}{2}$ 附近摆动，呈现一定的稳定性 C、一定不是 $\frac{1}{2}$ D、随着m的增大，越来越接近 $\frac{1}{2}$

查看试题解析
8. 如图，电路图上有三个开关S₁ ， S₂ ， S₃和两个小灯泡L₁ ， L₂ ，随机闭合开关S₁ ， S₂ ， S₃中的两个，能让灯泡L₂发光的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
9. 同一元素中质子数相同，中子数不同的各种原子互为同位素，如 $_{6}^{12} C$ 与 $_{6}^{13} C$ 、 $_{8}^{16} O$ 与 $_{8}^{17} O$ ．在一次制取 $C O$ 的实验中， $_{6}^{12} C$ 与 $_{6}^{13} C$ 的原子个数比为 $2 ： 1$ ， $_{8}^{16} O$ 与 $_{8}^{17} O$ 的原子个数比为 $1 ： 1$ ，若实验恰好完全反应生成 $C O$ ，则反应生成 $_{6}^{12} C_{8}^{16} O$ 的概率（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
10. 将一枚飞镖投掷到如图所示的正六边形镖盘上（每次飞镖均落在镖盘上，且落在镖盘的任何一个点的机会都相等），飞镖落在阴影区域的概率为（　　）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{5}$

查看试题解析

二、填空题（每空4分，共24分）

11. 已如一个口袋中装有7个只有颜色不同的球，其中3个白球，4个黑球．若往口袋中再放入2个白球，求从口袋中随机取出一个白球的概率

查看试题解析
12. 某校准备从A，B两名女生和C，D两名男生中任选2人代表学校参加沈阳市初中生辩论赛，则所选代表恰好为1名女生和1名男生的概率是．

查看试题解析
13. 现有四张分别标有数字－1，－1，0，2的卡片，它们除数字外完全相同.把卡片背面朝上洗匀，从中随机抽取一张，记下数字不放回，再随机抽取一张，则两次抽出的卡片上的数字相同的概率是.

查看试题解析
14. 若标有A，B，C的三只灯笼按图示悬挂，每次摘取一只（摘B先摘C），直到摘完，则最后一只摘到B的概率是.

查看试题解析
15. 有四张正面分别标有数字﹣4，﹣3，﹣2，1，的不透明卡片，它们除数字不同外其他全部相同，现将它们背面朝上，洗匀后从中抽取一张，将该卡片上的数字记为a，放回后洗匀，再从中抽取一张，将该卡片上的数字记为b，则a，b使得二次函数y＝x²﹣（a+5）x+3当x≤1时y随x的增大而减小，且一元二次方程（a+2）x²+bx+1＝0有解的概率为．

查看试题解析
16. 在平面直角坐标系中,作OOAB,其中三个顶点分别是O(0,0),B(1,1),A( $x$ , $y$ ),其中点A,O,B不在同一直线上且-2≤ $x$ ≤2,-2≤ $y$ ≤2, $x$ , $y$ 均为整数，则所作OOAB为直角三角形的概率是.

查看试题解析

三、解答题（共8题，共66分）

17.

(1)、概念理解
嘉嘉和淇淇学习了随机事件的概率，老师留的作业中有一道判断题：①自然现象中，“太阳从东方升起”是必然事件；②成语“水中捞月”所描述的事件是随机事件；③若抽奖活动的中奖概率为 $\frac{1}{50}$ ，则抽奖50次必中奖1次．

真命题的序号是；

(2)、知识应用
嘉嘉和淇淇做化学实验，紫色石蕊试剂是一种常用的酸碱指示剂，通常情况下石蕊试剂遇酸溶液变红，遇碱溶液变蓝，遇中性溶液不变色．现有4瓶缺失标签的无色液体：蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液，其中白醋溶液、柠檬水溶液是酸性，食用碱溶液是碱性，蒸馏水是中性，两人各取了4个烧杯，分别倒入这4种不同的无色液体．

①嘉嘉将石蕊试剂滴入任意一个烧杯，呈现蓝色的概率是；

②淇淇随机取了两个烧杯，滴入石蕊试剂，用画树状图法或列表法求一杯变红、一杯变蓝的概率．

查看试题解析
18. 某乒乓球俱乐部有 $3$ 名男队员和 $3$ 名女队员可参加对外比赛，其中有 $1$ 名男队员和 $1$ 名女队员使用左手打球．现计划用这 $6$ 名队员组成混合双打组合．（以下简称混双组合：就是由一名男队员和一名女队员组成）

(1)、可以有多少种不同的混双组合？如果从这些组合中任选 $1$ 个参加比赛，那么选中的组合中正好有一名左手队员和一名右手队员的概率是多少？

(2)、实际运作中，通过各种组合之间的比赛，最终确定了 $3$ 个组合，其中有一个组合正好是男 $1$ 号与女 $1$ 号组成的（我们称为“一号组合”）．如果这三个组合通过抓阉（jiu）方式决定哪一组由张岩教练指导，直接写出“一号组合”选中张岩教练的概率是多少？

查看试题解析
19. 如图，程序员在数轴上设计了A、B两个质点，它们分别位于-6和9的位置，现两点按照下述规则进行移动：每次移动的规则x分别掷两次正方体骰子，观察向上面的点数：
①若两次向上面的点数均为偶数，则A点向右移动1个单位，B点向左移2个单位；
②若两次向上面的点数均为奇数，则A点向左移动2个单位，B点向左移动5个单位；
③若两次向上面的点数为一奇一偶，则A点向右移动5个单位，B点向右移2个单位．

(1)、经过第一次移动，求B点移动到4的概率；

(2)、从如图所示的位置开始，在完成的12次移动中，发现正方体骰子向上面的点数均为偶数或奇数，设正方体骰子向上面的点数均为偶数的次数为a，若A点最终的位置对应的数为b，请用含a的代数式表示b，并求当A点落在原点时，求此时B点表示的数；

(3)、从如图所示的位置开始，经过x次移动后，若 $A B = 3$ ，求x的值．

查看试题解析
20. 从2021年秋季开学以来，全国各地中小学都开始实行了“双减政策”．为了解家长们对“双减政策”的了解情况，从某校1200名家长中随机抽取部分家长进行问卷调查，调直评价结果分为“了解较少”“基本了解”“了解较多”“非常了解”四类，并根据调查结果绘制出如图所示的两幅不完整的统计图．

(1)、本次抽取家长共有人，扇形图中“基本了解”所占扇形的圆心角是；

(2)、估计此校“非常了解”和“了解较多”的家长共有多少人?

(3)、学校计划从“了解较少”的家长中抽取1位初一学生家长，1位初二学生家长，2位初三学生家长参加培训，若从这4位家长中随机选取两人作为代表，请通过列表或面树状图的方法求所选出的两位家长既有初一家长，又有初二家长的概率．

查看试题解析
21. 4月23日是世界读书日，某学校为增进同学们对中国古诗词的热爱，举行“春季校园飞花令”专场比赛．在预选赛后，学校对参赛同学获奖情况进行统计，绘制了如下两幅不完整的统计图．请结合图中相关数据解答下列问题：

(1)、请将条形统计图补充完整；

(2)、在扇形统计图中，“三等奖”所对应的扇形圆心角的度数为；

(3)、若获得一等奖的同学中有 $\frac{1}{4}$ 来自七年级， $\frac{1}{2}$ 来自九年级，其余的来自八年级，学校决定从获得一等奖的同学中任选两名同学参加全市诗词大会比赛，请通过列表或树状图方法求所选两名同学中，恰好都来自九年级的概率．

查看试题解析
22. 在甲、乙两名同学中选拔一人参加“中华好诗调”大赛，在相同的测试条件下，两人5次测试成绩（单位，分）如下：
甲：78，85，81，84，82
乙：88，79，90，81，72．
回答下列问题：

(1)、甲成绩的平均数是，乙成绩的平均数是；

(2)、分别计算 $S_{甲}^{2}$ ， $S_{乙}^{2}$ ，你认为选拔谁参加比赛更合适，说明理由；

(3)、如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析，求抽到的两个人的成绩都大于80分的概率．

查看试题解析
23. 今年疫情期间，为防止疫情扩散，人们见面的机会少了，但是随着通讯技术迅猛发展，人与人之间的沟通方式更多样、便捷，为此，孙老师设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种）进行调查.将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：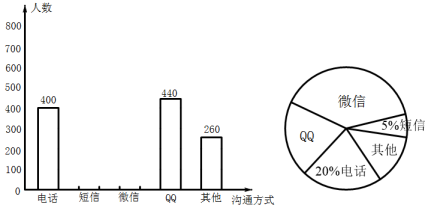

(1)、这次参与调查的共有人；在扇形统计图中，表示“微信”的扇形圆心角的度数为；其它沟通方式所占的百分比为．

(2)、将条形统计图补充完整；

(3)、如果我国有13亿人在使用手机．
①请估计最喜欢用“微信”进行沟通的人数；
②在全国使用手机的人中随机抽取一人，用频率估计概率，求抽取的恰好使用“QQ”的概率是多少？

查看试题解析

24. 某学校为落实立德树人根本任务，使每个学生都能得到全面而个性的发展，特举办了“科学竞赛”活动，甲、乙两个班学生的成绩统计如下：

分数/分	50	60	70	80	90	100
甲班人数/人	2	5	10	18	14	1
乙班人数/人	4	4	16	4	18	4

活动规定：以60分为及格线，并分别设置了一、二、三等奖，100分为一等奖，90分为二等奖，80分为三等奖．小亮分别计算了两个班的平均分和方差，得： ${\bar{x}}_{甲} = 78$ ， ${\bar{x}}_{乙} = 78$ ， ${\bar{x}}_{甲}^{2} = 128$ ， ${\bar{x}}_{乙}^{2} = 200$ ．请你根据以上材料回答下列问题．

(1)、甲、乙两个班的中位数和众数分别是多少？

(2)、你认为甲、乙两个班哪个班的成绩更优秀？为什么？

(3)、该校从得100分的两男三女5人中，随机选取2人参加教育局组织的竞赛，请你用列表或画树状图的方法，求出恰好选取一男一女参赛的概率．

查看试题解析

2023年浙教版数学九年级上册2.2 简单事件的概率 同步测试（培优版）

一、单选题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学九年级上册2.2 简单事件的概率同步测试（培优版）