2023年浙教版数学八年级上册1.6 尺规作图 同步测试(提高版)
试卷更新日期:2023-08-13 类型:同步测试
一、选择题(每题3分,共20分)
-
1.
某学习小组中有甲、乙、丙、丁四位同学,为解决尺规作图:“过直线AB外一点M,作一直线垂直于直线AB”,各自提供了如下四种方案,其中正确的是( )
 A、甲、乙 B、乙、丙 C、丙、丁 D、甲、乙、丙2. 下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线。则对应作法错误的是( )
A、甲、乙 B、乙、丙 C、丙、丁 D、甲、乙、丙2. 下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线。则对应作法错误的是( ) A、① B、② C、③ D、④3. 已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )
A、① B、② C、③ D、④3. 已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( ) A、①② B、①③ C、②③ D、①②③4. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、
A、①② B、①③ C、②③ D、①②③4. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、 B、
B、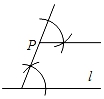 C、
C、 D、
D、 5. 如图是作△ABC的作图痕迹,则此作图的已知条件是( )
5. 如图是作△ABC的作图痕迹,则此作图的已知条件是( ) A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角6. 已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序依次为( )
A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角6. 已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序依次为( )①延长CD到B,使BD=CD;②连接AB;③作△ADC,使DC=a,AC=b,AD=m.
A、③①② B、①②③ C、②③① D、③②①7. 下列各条件中,不能作出唯一三角形的是( )A、已知两边和夹角 B、已知两边和其中一边的对角 C、已知两角和夹边 D、已知三边8. 内找一点P,使P到B、C两点的距离相等,并且P到C的距离等于A到C的距离.下列尺规作图正确的是( )A、 B、
B、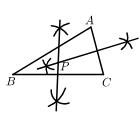 C、
C、 D、
D、 9. 如图,用直尺和圆规作图,以点O为圆心,适当长为半径画弧,分别交OB , OA于点E、D , 再分别以点E、D为圆心,大于ED的长为半径画弧,两弧交于点C , 连接OC , 则△ODC≌OEC的理由是( )
9. 如图,用直尺和圆规作图,以点O为圆心,适当长为半径画弧,分别交OB , OA于点E、D , 再分别以点E、D为圆心,大于ED的长为半径画弧,两弧交于点C , 连接OC , 则△ODC≌OEC的理由是( ) A、SSS B、SAS C、AAS D、ASA10. 在以下图形中,根据尺规作图痕迹,不能判断射线AD平分∠BAC的是( )
A、SSS B、SAS C、AAS D、ASA10. 在以下图形中,根据尺规作图痕迹,不能判断射线AD平分∠BAC的是( ) A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题(每空2分,共16分)
-
11.
下列语句表示的图形是(只填序号)
①过点O的三条直线与另条一直线分别相交于点B、C、D三点:
②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD:
③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点:
 12. 如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC。由这种作图方法得到的△D′O′C′和△DOC全等的依据是(写出全等判定方法的简写).
12. 如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC。由这种作图方法得到的△D′O′C′和△DOC全等的依据是(写出全等判定方法的简写).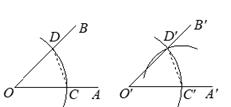 13. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.
13. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.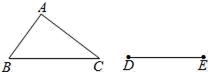 14. 已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c.①以点B为圆心,c为半径圆弧;②连接AB,AC;③作BC=a;④以C点为圆心,b为半径画弧,两弧交于点A.作法的合理顺序是15.
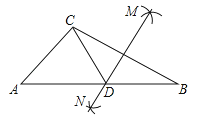
14. 已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c.①以点B为圆心,c为半径圆弧;②连接AB,AC;③作BC=a;④以C点为圆心,b为半径画弧,两弧交于点A.作法的合理顺序是15.如图,在△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于M,N两点;
②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为 .
 16.
16.如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F,为圆心,大于 长为半径作圆弧,两弧交于点G,作射线BG交CD于点H。若∠D=116°,则∠DHB的大小为°。

三、作图题(共14题,共84分)
-
17. 请你用直尺和圆规作图(要求:不必写作法,但要保留作图痕迹).已知:∠AOB,点M、N.求作:点P,使点P到OA、OB的距离相等,且PM=PN.
 18. 已知:两边及其夹角,线段 , , .
18. 已知:两边及其夹角,线段 , , .求作: ,使 , ,(用尺规作图,保留作图痕迹,不写作法).
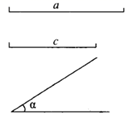
请你根据所学的知识,说明尺规作图作出 ,用到的是三角形全等判定定理中的_▲_,作出的 是唯一的,依据是三角形全等判定定理中的_▲_.
19. 如图,已知. (1)、尺规作出角平分线;(2)、尺规作中线;(3)、作边的高线.20. 如图,已知线段a,b,c.用直尺和圆规作△ABC,使BC=a, AC=b,AB=c.
(1)、尺规作出角平分线;(2)、尺规作中线;(3)、作边的高线.20. 如图,已知线段a,b,c.用直尺和圆规作△ABC,使BC=a, AC=b,AB=c. 21. 如图,在 中,点D在边 的延长线上.完成下面的尺规作图(保留作图痕迹,不写作法):
21. 如图,在 中,点D在边 的延长线上.完成下面的尺规作图(保留作图痕迹,不写作法):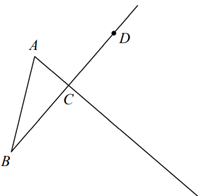 (1)、作边 的中点M.(2)、作 ,且点E在线段 的延长线上.22. 如图,中, , .
(1)、作边 的中点M.(2)、作 ,且点E在线段 的延长线上.22. 如图,中, , . (1)、用尺规作的平分线交于点D.(保留作图痕迹,不要求写作法);(2)、求的度数.23. 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.(1)、在图①中,画一个三角形,使它的三边长都是有理数;
(1)、用尺规作的平分线交于点D.(保留作图痕迹,不要求写作法);(2)、求的度数.23. 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.(1)、在图①中,画一个三角形,使它的三边长都是有理数;
图①
(2)、在图②中,画一个直角三角形,使它们的三边长都是无理数.
图②
24. 如图,在 8×6 的网格中,每个小正方形的边长均为一个单位. (1)、在图1中画出以BC为一边,面积为12的等腰三角形.(2)、在图 2中画出△ABC 的角平分线 BE.(△ABC 的三个顶点都在格点上,请按要求完成下列作图:①仅用无刻度的直尺,且不能用直尺中的直角;②保留作图痕迹;③标注相关字母.)25. 在4×4的网格中,每个小正方形的边长为1,请在甲,乙,丙三个方格图中,分别按照要求画一个格点三角形(三个顶点都在格点上的三角形叫格点三角形)
(1)、在图1中画出以BC为一边,面积为12的等腰三角形.(2)、在图 2中画出△ABC 的角平分线 BE.(△ABC 的三个顶点都在格点上,请按要求完成下列作图:①仅用无刻度的直尺,且不能用直尺中的直角;②保留作图痕迹;③标注相关字母.)25. 在4×4的网格中,每个小正方形的边长为1,请在甲,乙,丙三个方格图中,分别按照要求画一个格点三角形(三个顶点都在格点上的三角形叫格点三角形)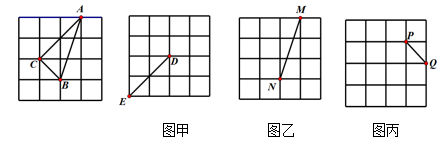 (1)、请在图甲中作△DEF与△ABC全等(2)、请在图乙中作格点三角形与△ABC全等,且所作的三角形有一条边经过MN的中点.(3)、请在图丙中作格点△PQR与△ABC不全等但面积相等26.
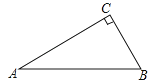
(1)、请在图甲中作△DEF与△ABC全等(2)、请在图乙中作格点三角形与△ABC全等,且所作的三角形有一条边经过MN的中点.(3)、请在图丙中作格点△PQR与△ABC不全等但面积相等26.如图,在△ABC中,∠C=90°.
(1)用尺规作图法作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连结BD,若BD平分∠CBA,求∠A的度数.
 27. 如图,在Rt△ABC中,∠C=90°,AC<BC.
27. 如图,在Rt△ABC中,∠C=90°,AC<BC.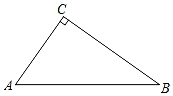 (1)、动手操作:要求尺规作图,不写作法,但保留作图痕迹.
(1)、动手操作:要求尺规作图,不写作法,但保留作图痕迹.①作出AB的垂直平分线MN,MN分别与AB交于点D,与BC交于点E.
②过点B作BF垂直于AE,垂足为F.
(2)、推理证明:求证AC=BF.28. “综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.(1)、用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.(2)、用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹).
 29.
29.如图,在方格纸中的三个顶点及A、B、C、D、E五个点都在小方格的顶点上.现以A、B、C、D、E中的三个点为顶点画三角形.
 (1)、在图甲中画出一个三角形与△PQR全等;(2)、在图乙中画出一个三角形与△PQR面积相等但不全等30. 解决下列两个问题:
(1)、在图甲中画出一个三角形与△PQR全等;(2)、在图乙中画出一个三角形与△PQR面积相等但不全等30. 解决下列两个问题: (1)、如图1,在△ABC中,AB=3,AC=4,BC=5.EF垂直且平分BC.点P在直线EF上,直接写出PA+PB的最小值,并在图中标出当PA+PB取最小值时点P的位置;
(1)、如图1,在△ABC中,AB=3,AC=4,BC=5.EF垂直且平分BC.点P在直线EF上,直接写出PA+PB的最小值,并在图中标出当PA+PB取最小值时点P的位置;解:PA+PB的最小值为 .
(2)、如图2.点M、N在∠BAC的内部,请在∠BAC的内部求作一点P,使得点P到∠BAC两边的距离相等,且使PM=PN.(尺规作图,保留作图痕迹,无需证明)