2023年浙教版数学八年级上册1.6 尺规作图 同步测试(培优版)
试卷更新日期:2023-08-13 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图, 在 中, , 在BC上取一点P, 使得 .根据圆规作图的痕迹,可以用直尺成功找到点P的是( )
2. 如图, 在 中, , 在BC上取一点P, 使得 .根据圆规作图的痕迹,可以用直尺成功找到点P的是( ) A、
A、 B、
B、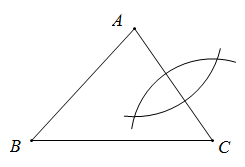 C、
C、 D、
D、 3. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.
3. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.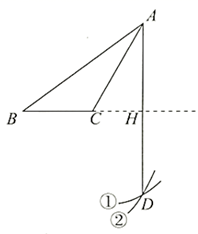
步骤1:以 为圆心, 长为半径画弧①;
步骤2:以 为圆心, 长为半径画弧②,交弧①于点 ;
步骤3:连接 ,交 的延长线于点 .
则下列说法错误的是( )
A、 是 中 边上的高 B、 C、 平分 D、作图依据是:①两点确定一条直线;②到线段两端点距离相等的点在线段的垂直平分线上4. 下面是教师出示的作图题.已知:线段 , ,小明用如图所示的方法作 ,使 , 上的高 .
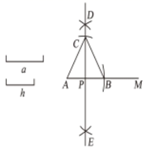
作法:①作射线 ,以点 为圆心、 ※ 为半径画弧,交射线 于点 ;②分别以点 , 为圆心、 △ 为半径画弧,两弧交于点 , ;③作直线 ,交 于点 ;④以点 为圆心、 为半径在 上方画孤,交直线 于点 ,连接 , .
对于横线上符号代表的内容,下列说法错误的是( )
A、※代表“线段a的长” B、△代表“任意长” C、△代表“大于 的长” D、 代表“线段 的长”5. 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1∶以C为圆心,CA为半径画弧①;
步骤2∶以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3∶连接AD,交BC延长线于点H.
下列叙述正确的是( )
 A、BH垂直平分线段AD B、AC平分∠BAD C、S△ABC=BC⋅AH D、AB=AD6. 下面是黑板上出示的尺规作图题,需要回答符号代表的内容( )
A、BH垂直平分线段AD B、AC平分∠BAD C、S△ABC=BC⋅AH D、AB=AD6. 下面是黑板上出示的尺规作图题,需要回答符号代表的内容( )如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB作法:(1)以●为圆心,任意长为半径画弧,分别交OA、OB于点P、Q;
(2)作射线EG,并以点E为圆心◎长为半径画弧交EG于点D;
(3)以点D为圆心⊙长为半径画弧交(2)步中所画弧于点F;
(4)作 , ∠DEF即为所求作的角.
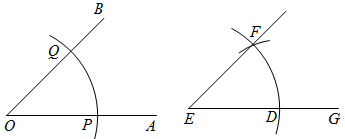 A、●表示点E B、◎表示PQ C、⊙表示OQ D、表示射线EF7. 如图,利用内错角相等,两直线平行,我们可以用尺规作图的方法,过的边上一点作的平行线 . 有以下顺序错误的作图步骤:①作射线;②以O为圆心,以任意长为半径画圆弧,分别交、于点C、D;③以F为圆心,长为半径画圆弧,交前面的圆弧于点G;④在边上取一点E,以E为圆心,长为半径画圆弧,交于点F.这些作图步骤的正确顺序为( )
A、●表示点E B、◎表示PQ C、⊙表示OQ D、表示射线EF7. 如图,利用内错角相等,两直线平行,我们可以用尺规作图的方法,过的边上一点作的平行线 . 有以下顺序错误的作图步骤:①作射线;②以O为圆心,以任意长为半径画圆弧,分别交、于点C、D;③以F为圆心,长为半径画圆弧,交前面的圆弧于点G;④在边上取一点E,以E为圆心,长为半径画圆弧,交于点F.这些作图步骤的正确顺序为( ) A、①②③④ B、③②④① C、②④③① D、④③①②8. 如图是三个基本作图的作图痕迹,关于①,②,③,④四条弧下列说法中错误的是( )
A、①②③④ B、③②④① C、②④③① D、④③①②8. 如图是三个基本作图的作图痕迹,关于①,②,③,④四条弧下列说法中错误的是( ) A、弧①是以点O为圆心,以任意长为半径所作的弧 B、弧②是以点B为圆心,以任意长为半径所作的弧 C、弧③是以点A为圆心,以大于的长为半径所作的弧 D、弧④是以点C为圆心,以大于的长为半径所作的弧9. 如图的中, , 且为上一点.今打算在上找一点 , 在上找一点 , 使得与全等,以下是甲、乙两人的作法:
A、弧①是以点O为圆心,以任意长为半径所作的弧 B、弧②是以点B为圆心,以任意长为半径所作的弧 C、弧③是以点A为圆心,以大于的长为半径所作的弧 D、弧④是以点C为圆心,以大于的长为半径所作的弧9. 如图的中, , 且为上一点.今打算在上找一点 , 在上找一点 , 使得与全等,以下是甲、乙两人的作法:甲连接 , 作的中垂线分别交、于点、点,则、两点即为所求
乙过作与平行的直线交于点,过作与平行的直线交于点,则、两点即为所求
对于甲、乙两人的作法,下列判断何者正确?( )
 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确10. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若的周长为 , 则的周长为( )
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确10. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若的周长为 , 则的周长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,在中, , 利用尺规在上分别截取;分别以点M,N为圆心,大于的长为半径作弧,两弧在内部交于点E,作射线交于点F,若 , 点H为线段上的一动点,则的最小值是 .
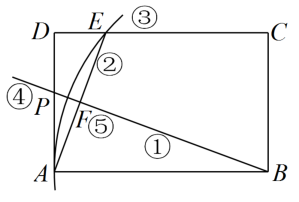
 12. 如图,长方形中, , P为上一动点,将点A沿翻折至点E,请画出点E恰好落在边时,点P的位置.我们有如下作图:①表示射线 , ②表示线段 , ③表示以B为圆心,为半径的弧,④表示射线与的交点P,⑤表示线段的中点F.请写出正确的作图顺序 . (只填序号)
12. 如图,长方形中, , P为上一动点,将点A沿翻折至点E,请画出点E恰好落在边时,点P的位置.我们有如下作图:①表示射线 , ②表示线段 , ③表示以B为圆心,为半径的弧,④表示射线与的交点P,⑤表示线段的中点F.请写出正确的作图顺序 . (只填序号)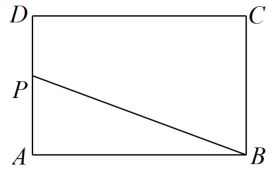
 13. 如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形。图中 是格点三角形,请你找出方格中所有与 全等,且以A为顶点的格点三角形.这样的三角形共有个( 除外).
13. 如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形。图中 是格点三角形,请你找出方格中所有与 全等,且以A为顶点的格点三角形.这样的三角形共有个( 除外). 14. 如图,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
14. 如图,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
①两点确定一条直线;②两点之间线段最短;③垂线段最短.(1)、从码头A到火车站B怎样走最近,请画图,并选择理由 (填序号).(2)、从码头A到铁路a怎样走最近,请画图,并选择理由 (填序号).15. 如图,已知线段 ,其垂直平分线 的作法如下:①分别以点 和点 为圆心, 长为半径画弧,两弧相交于 , 两点;②作直线 .上述作法中 满足的条作为 1.(填“ ”,“ ”或“ ”) 16. 利用尺规作三角形,有三种基本类型:
16. 利用尺规作三角形,有三种基本类型:⑴已知三角形的两边及其夹角,求作符合要求的三角形,其作图依据是“”;
⑵已知三角形的两角及其夹边,求作符合要求的三角形,其作图依据是“”;
⑶已知三角形的三边,求作符合要求的三角形,其作图依据是“”.
三、作图题(共8题,共72分)
-
17. 如图,在中,
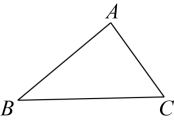 (1)、作的角平分线交于 , 作线段的垂直平分线分别交于 , 交于 , 垂足为(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,连接 , 则与边的位置关系是。18. 图①、图②、图③均是由小正方形组成的的网格,的三个顶点A、B、C均在格点(网格线的交点)上,请按要求在给定的网格中,仅用无刻度的直尺,分别按下列要求作图,保留作图痕迹,不写画法.
(1)、作的角平分线交于 , 作线段的垂直平分线分别交于 , 交于 , 垂足为(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,连接 , 则与边的位置关系是。18. 图①、图②、图③均是由小正方形组成的的网格,的三个顶点A、B、C均在格点(网格线的交点)上,请按要求在给定的网格中,仅用无刻度的直尺,分别按下列要求作图,保留作图痕迹,不写画法. (1)、在图①中的上确定一点D , 连结 , 使 .(2)、在图②中的上确定一点E , 连结 , 使 .(3)、在图③中的上确定一点F , 连结 , 使 .19. 如图,测绘平面上有两个点A,B.应用量角器和圆规完成下列画图或测量:
(1)、在图①中的上确定一点D , 连结 , 使 .(2)、在图②中的上确定一点E , 连结 , 使 .(3)、在图③中的上确定一点F , 连结 , 使 .19. 如图,测绘平面上有两个点A,B.应用量角器和圆规完成下列画图或测量:
①连接AB,点C在点B北偏东30°方向上,且BC=2AB,作出点C(保留作图痕迹);
②在(1)所作图中,D为BC的中点,连接AD,AC,画出∠ADC的角平分线DE交AC于点E;
③在①②所作图中,用量角器测量∠BDE的大小(精确到度).
20. 课堂上,老师在黑板上出了一道题:在同一平面内,若∠AOB=70°,∠BOC=15°24′36″,求∠AOC的度数.下面是七年级同学小明在黑板上写的解题过程:
解:根据题意可画出图(如图1)


因为∠AOB=70°,∠BOC=15°24′36″,
所以∠AOC=∠AOB+∠BOC
=70°+15°24′36″
=85°24′36″
即得到∠AOC=85°24′36″
同学们在下面议论,都说小明解答不全面,还有另一种情况.请按下列要求完成这道题的求解.
(1)、依照图1,用尺规作图的方法将另一种解法的图形在图2中补充完整.(2)、结合第(1)小题的图形写出求∠AOC的度数的完整过程.21. 仅用无刻度的直尺作出符合下列要求的图形.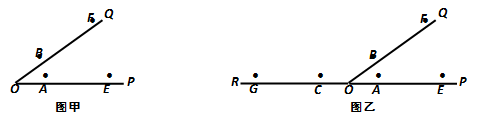 (1)、如图甲,在射线OP、OQ上已截取OA=OB,OE=OF.试过点O作射线OM,使得OM将∠POQ平分;(2)、如图乙,在射线OP、OQ、OR上已截取OA=OB=OC,OE=OF=OG(其中OP、OR在同一根直线上). 试过点O作一对射线OM、ON,使得OM⊥ON.22. 综合题。(1)、如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.
(1)、如图甲,在射线OP、OQ上已截取OA=OB,OE=OF.试过点O作射线OM,使得OM将∠POQ平分;(2)、如图乙,在射线OP、OQ、OR上已截取OA=OB=OC,OE=OF=OG(其中OP、OR在同一根直线上). 试过点O作一对射线OM、ON,使得OM⊥ON.22. 综合题。(1)、如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.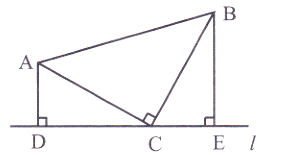 (2)、如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)
(2)、如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹) (3)、若AB=10,CD=3,求△ABD的面积.23. 阅读下列材料,并完成相应的学习任务:
(3)、若AB=10,CD=3,求△ABD的面积.23. 阅读下列材料,并完成相应的学习任务:一次有意义的动手实践活动——在格点图中巧作角平分线
实践背景
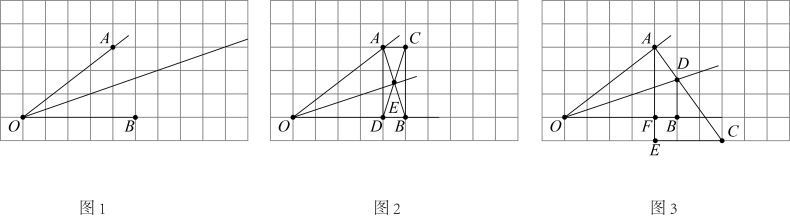
在一次动手实践课上,老师提出如下问题:在如图1所示由边长为1的小正方形组成的格点图中,点 , , 都在小正方形的顶点处,仅用无刻度的直尺作出的角平分线.
成果展示
小明、小亮展示了如下作法:
小明:如图2,在格点图中取格点 , . 连接 , 交于点 . 作出射线 .
∵四边形是矩形,∴(依据1).
∵ , ∴平分 .
小亮:如图3,在格点图中取格点 . 连接 , 与小正方形的边交于点 . 则 .
∵ , .
∴(依据2).
∴ , 即平分 .
学习任务:
(1)、实践反思:①请填写出上述材料中的依据1和依据2.
依据1: ▲ ;依据2: ▲ .
②请根据小亮的作法,证明 .
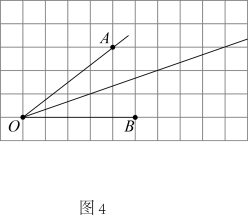
(2)、创新再探请你根据实践背景问题要求,采用不同于小明和小亮的作法,描出作图过程中的所取得的点,作出的角平分线(不写作法,不需要说明理由).
 24. 探索角的平分线的画法.(1)、画法1:利用直尺和圆规
24. 探索角的平分线的画法.(1)、画法1:利用直尺和圆规请在图中用直尺和圆规画出 的平分线 ;(不写画法不需证明,保留作图痕迹)
 (2)、画法2:利用等宽直尺.
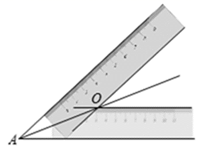
(2)、画法2:利用等宽直尺.如图,将一把等宽直尺的一边依次落在 的两条边上,再过另一边分别画直线,两条直线相交于点O.画射线 ,则射线 是 的平分线.这种角的平分线的画法依据的是______.
 A、 B、 C、 D、(3)、画法3:利用刻度尺
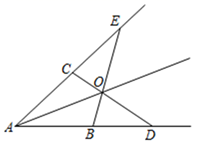
A、 B、 C、 D、(3)、画法3:利用刻度尺已知:如图,在 的两条边上分别画 , ,连接 、 ,交点为点O,画射线 .
求证: 是 的平分线.
 (4)、画法4:利用你手里带有刻度的一块直角三角尺,设计一种与上述画法不同的角的平分线的画法.请在图中画出 的平分线 ,写出画法,并加以证明.
(4)、画法4:利用你手里带有刻度的一块直角三角尺,设计一种与上述画法不同的角的平分线的画法.请在图中画出 的平分线 ,写出画法,并加以证明.